Об учебниках по геометрии и теоремах в них. Признаки параллельных и скрещивающихся прямых, параллельности прямой и плоскости
Содержание
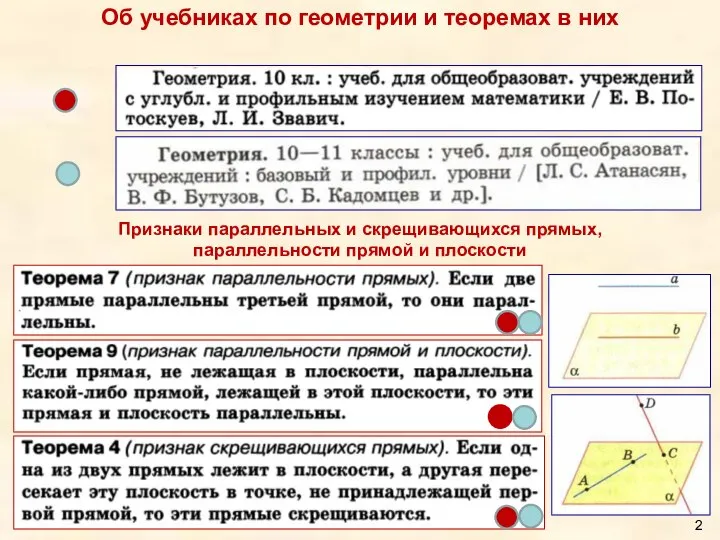
- 2. Об учебниках по геометрии и теоремах в них Признаки параллельных и скрещивающихся прямых, параллельности прямой и
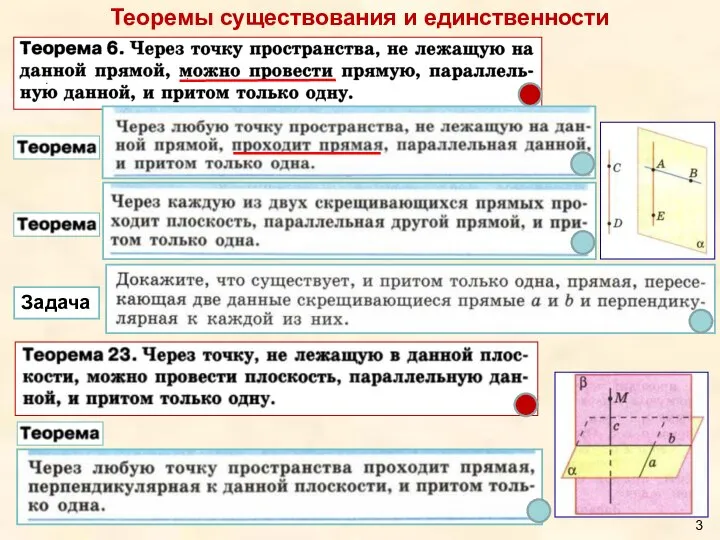
- 3. Теоремы существования и единственности Задача
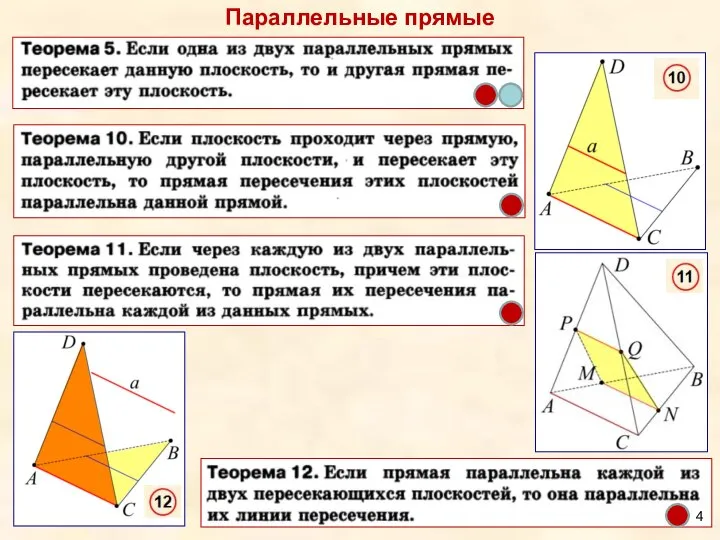
- 4. Параллельные прямые
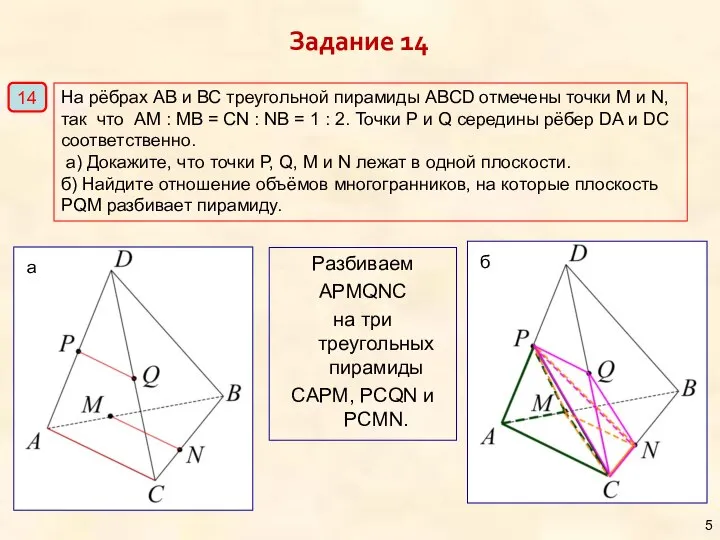
- 5. Разбиваем APMQNC на три треугольных пирамиды CAPM, PCQN и PCMN. На рёбрах АВ и ВС треугольной
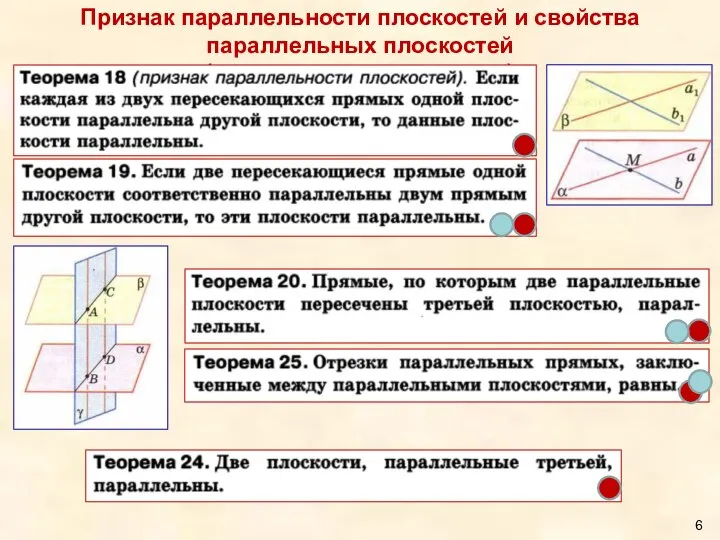
- 6. Признак параллельности плоскостей и свойства параллельных плоскостей (что должен знать эксперт)
- 7. Теорема о трех перпендикулярах
- 8. Демовариант. Решение задания 14 14
- 9. Перпендикулярность прямой и плоскости
- 10. ЕГЭ 2017 (основной экзамен) 9 15 13 14
- 11. Решение задания 14 14 ЕГЭ 2015
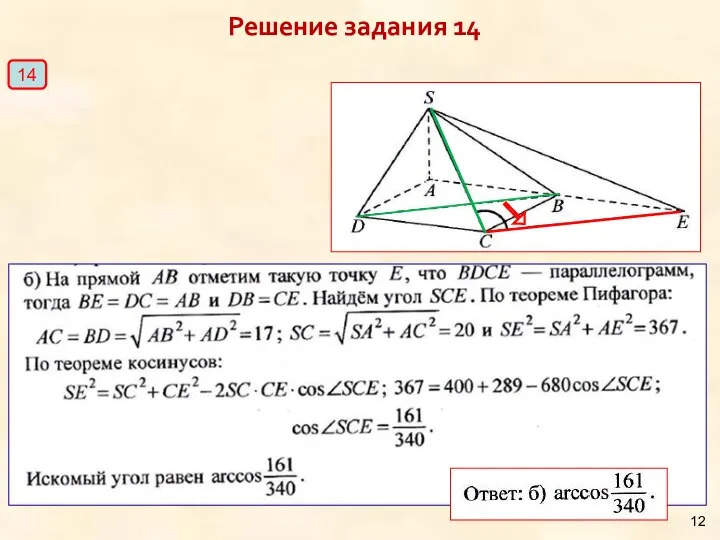
- 12. Решение задания 14 14
- 13. Перпендикулярность двух плоскостей
- 14. ЕГЭ 2017 (основной экзамен) 14
- 15. ЕГЭ 2017 (основной экзамен) Из точки Р опускаем перпендикуляры на АВ и DC. Они являются перпендикулярами
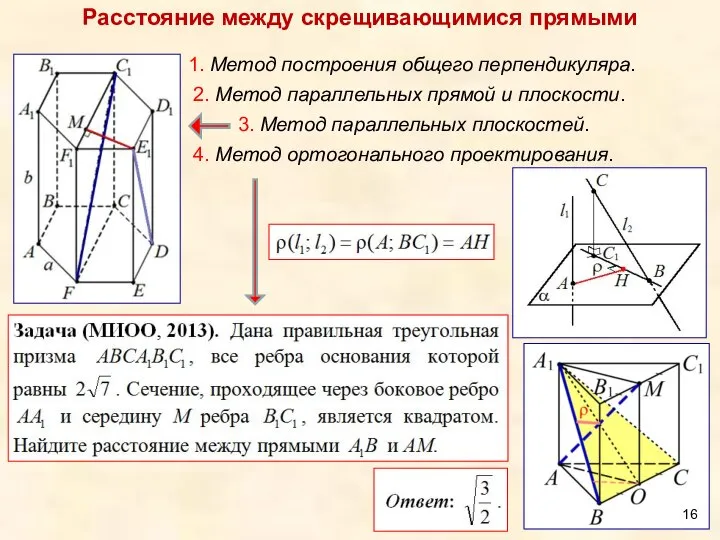
- 16. Расстояние между скрещивающимися прямыми 1. Метод построения общего перпендикуляра. 2. Метод параллельных прямой и плоскости. 3.
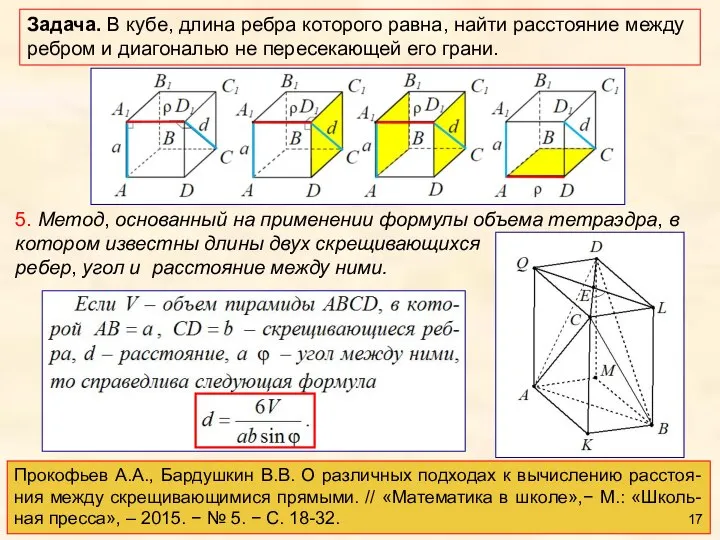
- 17. 5. Метод, основанный на применении формулы объема тетраэдра, в котором известны длины двух скрещивающихся ребер, угол
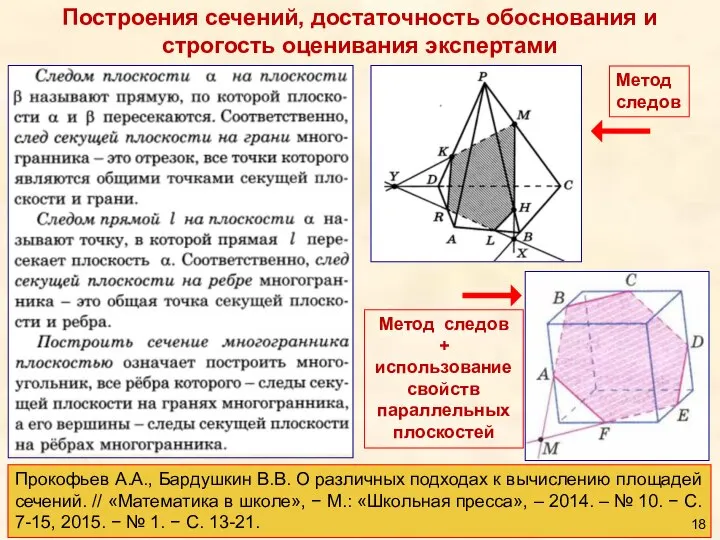
- 18. Построения сечений, достаточность обоснования и строгость оценивания экспертами Прокофьев А.А., Бардушкин В.В. О различных подходах к
- 19. Пример задания 14 14 ЕГЭ 2015
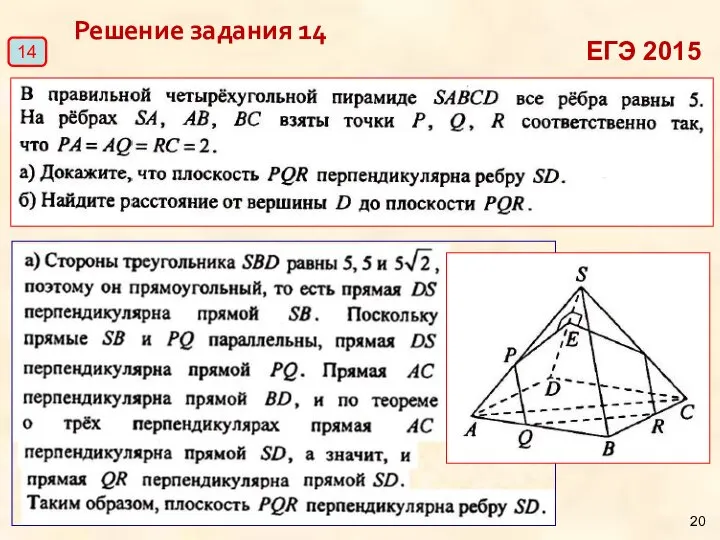
- 20. Решение задания 14 14 ЕГЭ 2015
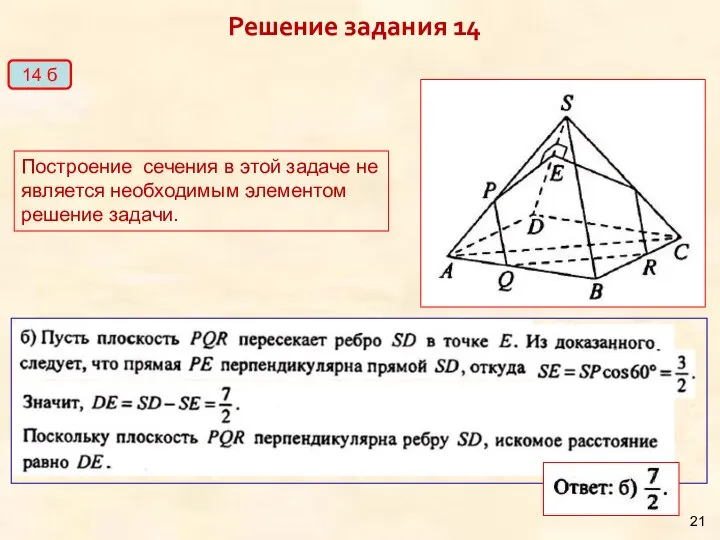
- 21. Решение задания 14 14 б Построение сечения в этой задаче не является необходимым элементом решение задачи.
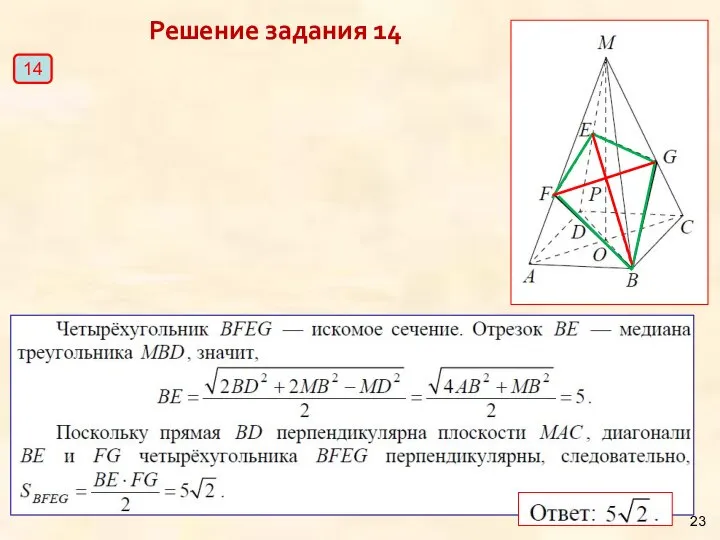
- 22. Решение задания 14 14 ЕГЭ 2013
- 23. Решение задания 14 14
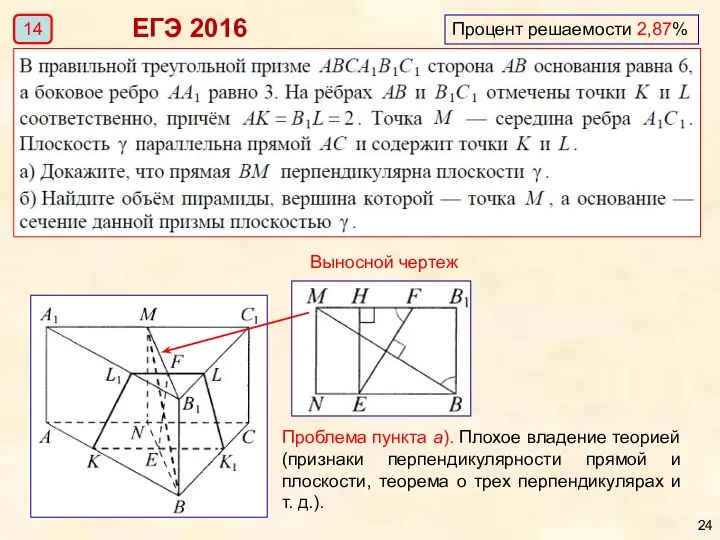
- 24. Процент решаемости 2,87% ЕГЭ 2016 Выносной чертеж 14 Проблема пункта а). Плохое владение теорией (признаки перпендикулярности
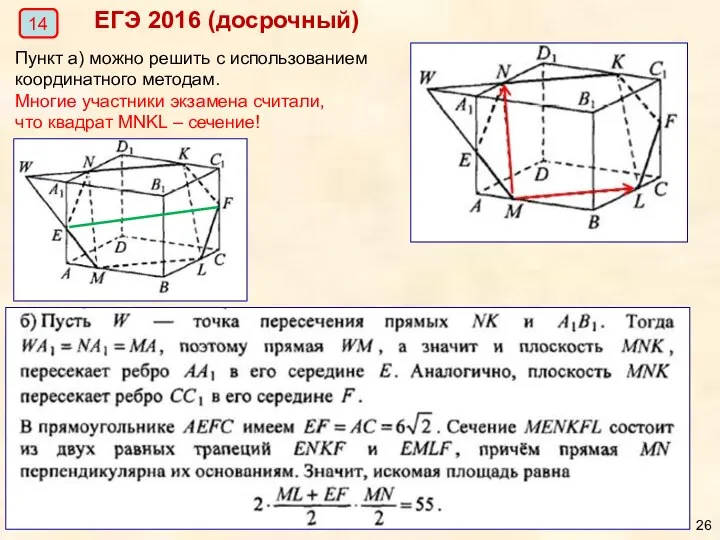
- 25. ЕГЭ 2016 (досрочный) 14
- 26. ЕГЭ 2016 (досрочный) 14 Пункт а) можно решить с использованием координатного методам. Многие участники экзамена считали,
- 27. Применение теоремы о площади ортогональной проекции Бардушкин В.В., Белов А.И., Ланцева И.А., Прокофьев А.А., Фадеичева Т.П.
- 28. Координатный метод
- 29. Бардушкин В.В., Корянов А.Г., Прокофьев А.А. Методы решения задач по теме «Двугранный угол. Угол между плоскостями».
- 30. О применении формул аналитической геометрии
- 32. Скачать презентацию















 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник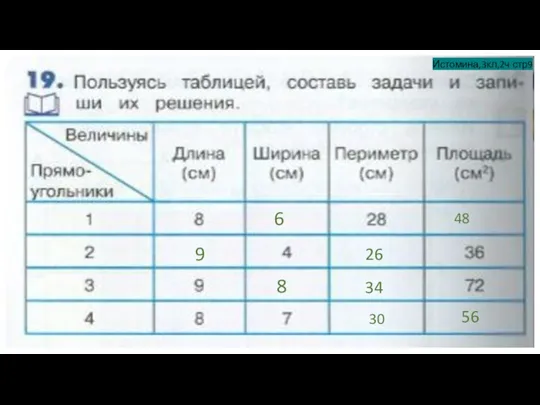 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика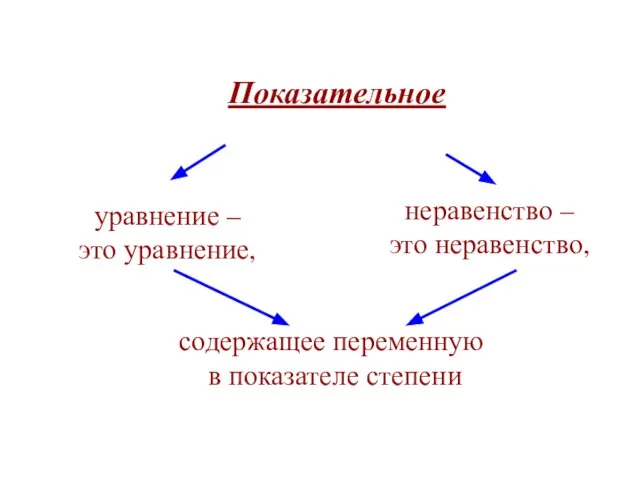 Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность