Урок 9-10 Відстань між двома точками на площині

Формули для визначення відстані між точками

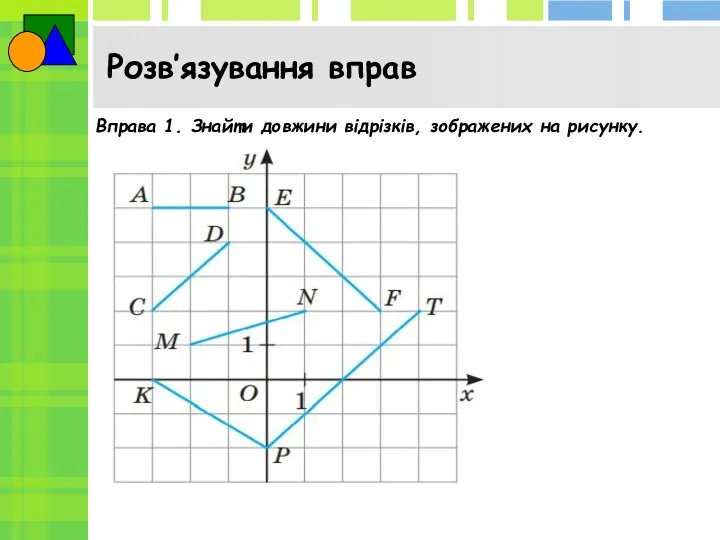
Розв’язування вправ
Вправа 1. Знайти довжини відрізків, зображених на рисунку.

Вправа 2. Знайдіть периметр ABC, якщо A(–2; 5), B(7; 8), C(2; –7).
Вправа 3. Дано трикутник ABC з вершинами A(–2; 5), B(6; 3), C(4; –3). Знайдіть довжини середніх ліній трикутника.

Вправа 4. Доведіть, що трикутник з вершинами:
а) A(–1; 1), B(2; –2), C(6; 2) — прямокутний;
б) M(–5; 2), N(3; 6), K(4; –6) — рівнобедрений.
Вправа 5. Знайдіть x, якщо:
а) AB = 2, A(2; 1), B(x; –1);
б) AB = 10, A(2x; 7), B(x; 1);
в) AB = 5, A(–1; x), B(2x; –3).

Також корисно розібрати розв’язання вправи 6

Домашнє завдання
Знайдіть довжини медіан ABC, якщо:
а) A(–4; –2), B(2; 6), C(4; 2);
б) A(–5; 1), B(–3; 5), C(–1; –1).
2. Доведіть, що трикутник з вершинами A(2; 3), B(–2; 1), C(0; –3) — рівнобедрений прямокутний.
3. На прямій y = 2x знайдіть точку, рівновіддалену від точок M(5; 2) і N(–1; 4).
4. Знайдіть радіус кола, описаного навколо ABC, якщо
A(–2; 4), B(–6; 4), C(–4; 2).
5. Доведіть, що точки M(–2; –1), N(2; 7), K(–1; 1) лежать на одній прямій. Знайдіть відношення довжин відрізків MK і KN.