Содержание
- 2. Джон Непер, изобретатель логарифмов Определение логарифмов и таблицу их значений впервые опубликовал в 1614 году шотландский
- 3. Примеры использования неравномерности логарифмической зависимости Акустика — интенсивность звука (децибелы). Отношение сигнал/шум в радиотехнике и электросвязи.
- 4. Логарифмическая спираль в природе Расположение семян на подсолнечнике Раковина наутилуса
- 5. Вычислите: Определение логарифма числа Логарифмом числа b>0 по основанию a (a≠1, a>0) называется показатель степени, в
- 6. Основное логарифмическое тождество , где a≠1, a>0, b>0 Вычислите:
- 7. При каких значениях х существует логарифм Х > 3 X X X R Не существует ни
- 8. Основные свойства логарифмов При любом a>0, a≠1 и любых x>0 и y>0 выполнены равенства: logₐ 1
- 9. 1. Логарифм произведения положительных чисел равен сумме логарифмов множителей. loga (bc) = loga b + loga
- 10. 2. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. loga b c =
- 11. 3. Логарифм степени с положительным основанием равен показателю степени, умноженному на логарифм основания log abr =
- 12. Исправьте ошибки:
- 13. Формула перехода от одного основания логарифма к другому
- 14. Десятичные логарифмы log10 a = lg a lg 10 = 1 lg 100 = lg 10²
- 15. Натуральный логарифм logе a = ln a ln e = 1 Натуральным логарифмом числа называют логарифм
- 16. Вычислить: log7 49; log3 1/81; log1/2 8; log4 1; lg 10000; lg 0,001; log6 3 +
- 18. Скачать презентацию















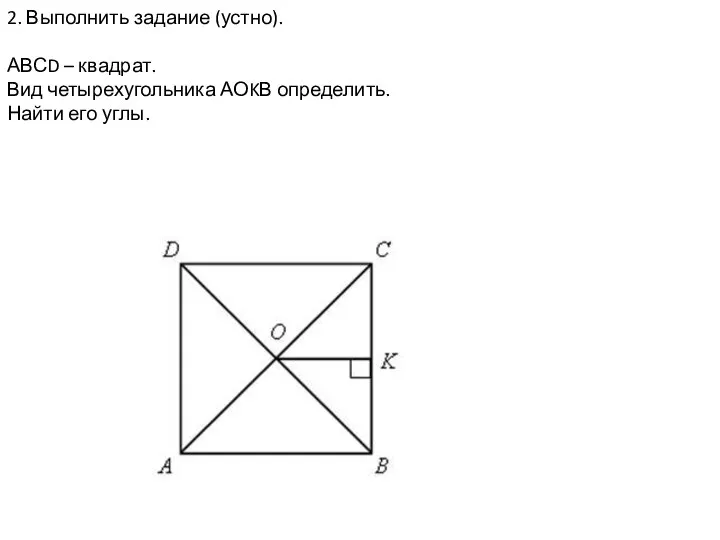 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи Математический язык
Математический язык Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ
Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ  Четные и нечетные числа
Четные и нечетные числа 1_urok_algebry_v_8_klasse
1_urok_algebry_v_8_klasse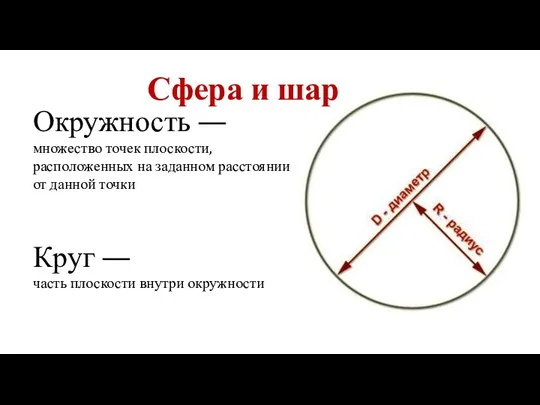 Сфера и шар
Сфера и шар Учимся складывать столбиком
Учимся складывать столбиком Работа переменной силы
Работа переменной силы Математическая логика и теория алгоритмов. Алгебра логики. Часть 2
Математическая логика и теория алгоритмов. Алгебра логики. Часть 2 Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Задачи по геометрии 11 класс
Задачи по геометрии 11 класс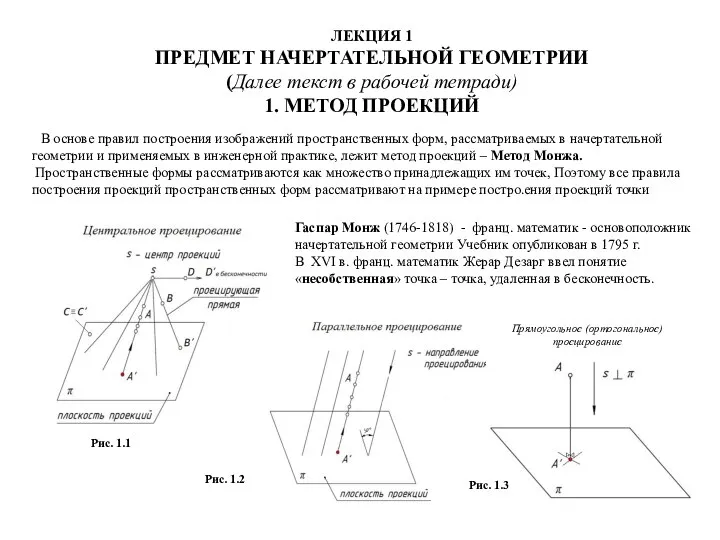 Предмет начертательной геометрии. Метод проекций. (Лекция 1)
Предмет начертательной геометрии. Метод проекций. (Лекция 1) Показательные неравенства
Показательные неравенства Интервальное оценивание
Интервальное оценивание Весёлый счёт
Весёлый счёт Функция нескольких действительных переменных. Условный экстремум
Функция нескольких действительных переменных. Условный экстремум Основы алгебры логики
Основы алгебры логики Человек трудолюбивый – самый счастливый– самый
Человек трудолюбивый – самый счастливый– самый Правила деления. (6 класс)
Правила деления. (6 класс) Преобразование графиков функций
Преобразование графиков функций Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Математический калейдоскоп. Мероприятие для учащихся 5 классов
Математический калейдоскоп. Мероприятие для учащихся 5 классов Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций B1. Практический расчет, оценка и прикидка
B1. Практический расчет, оценка и прикидка