Содержание
- 2. Под законом больших чисел (ЗБЧ) в широком смысле понимается общий принцип, согласно которому, по формулировке академика
- 3. Неравенство Маркова (лемма Чебышева) (1) Вероятность того, что случайная величина Х примет значение больше А, меньше
- 5. Неравенство Чебышева (2) Вероятность того, что случайная величина отклониться от своего математического ожидания на величину меньше
- 6. Неравенство Чебышева для некоторых случайных величин
- 7. Пример 2. (3)
- 8. Теорема Чебышева (6) Опуская доказательство, получаем неравенство (7) (6) (7) (8)
- 9. Хотя мы и не можем предсказать конкретное значение случайной величины, мы можем с вероятностью, близкой к
- 10. Примеры применения теоремы Чебышева в реальной жизни 1. Проведение измерений: при достаточно большом количестве измерений, например,
- 12. Теорема Бернулли и теорема Пуассона
- 13. Теорема Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, или статической вероятностью, полученной в
- 14. Центральная предельная теорема
- 15. (11)
- 16. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных
- 17. Математическая статистика Математическая статистика выделяется из теории вероятностей в самостоятельную область, хотя основные методы и приемы
- 18. В качестве реализации случайного явления или случайного события выступают так называемые статистические данные. В большинстве случаев
- 19. Пусть требуется изучить некоторую ГС. Для этого можно провести сплошное обследование. Однако если число объектов ГС
- 21. Если значения выборки записать в неубывающем порядке, то получим последовательность, называемую вариационным рядом, а x(i) называются
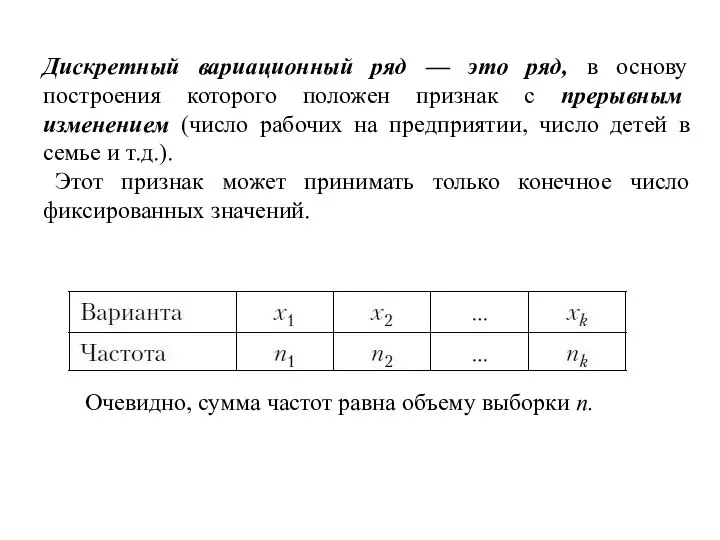
- 22. Дискретный вариационный ряд — это ряд, в основу построения которого положен признак с прерывным изменением (число
- 23. Если признак имеет непрерывное изменение, т.е. значения могут отличаться одно от другого на сколь угодно малую
- 24. Построение интервального ряд Относительной частотой называется величина где n — объем выборки, а ni — частота
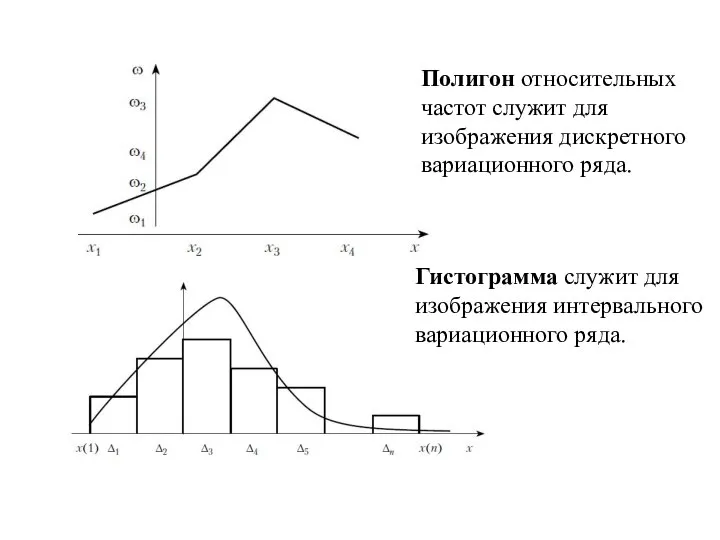
- 25. Полигон относительных частот служит для изображения дискретного вариационного ряда. Гистограмма служит для изображения интервального вариационного ряда.
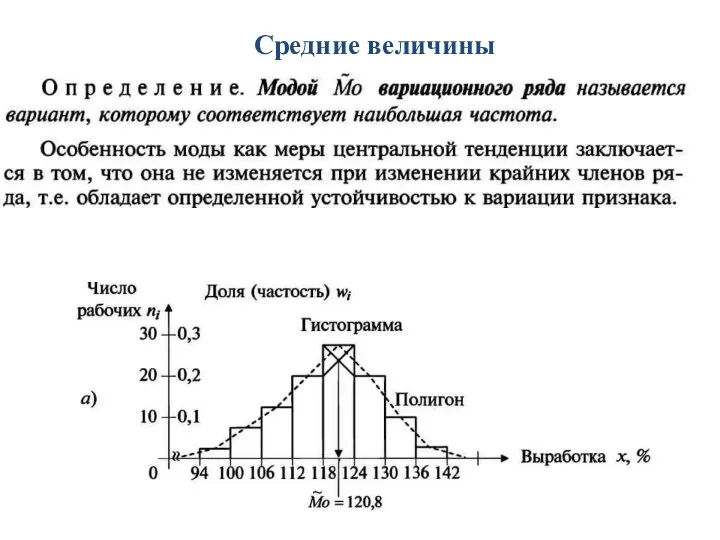
- 26. Числовые характеристики выборочного распределения назовем выборочными или эмпирическими характеристиками.
- 27. Средние величины
- 28. Средние величины
- 29. Средние величины
- 30. Показатели вариации
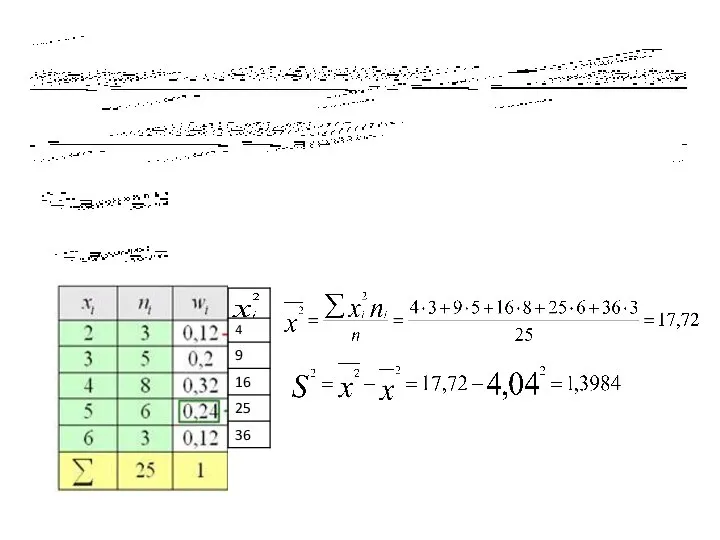
- 31. Если выборка представлена в виде интервального вариационного ряда, то для вычисления выборочных среднего и дисперсии вначале
- 32. Свойства дисперсии
- 36. Пример 1. Имеются данные о торгах акций некоторого акционерного общества на фондовой бирже. Количество проданных акций
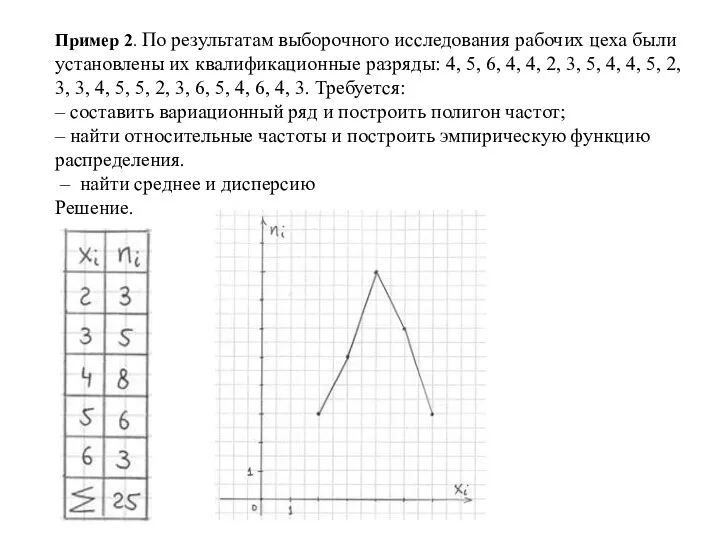
- 37. Пример 2. По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6,
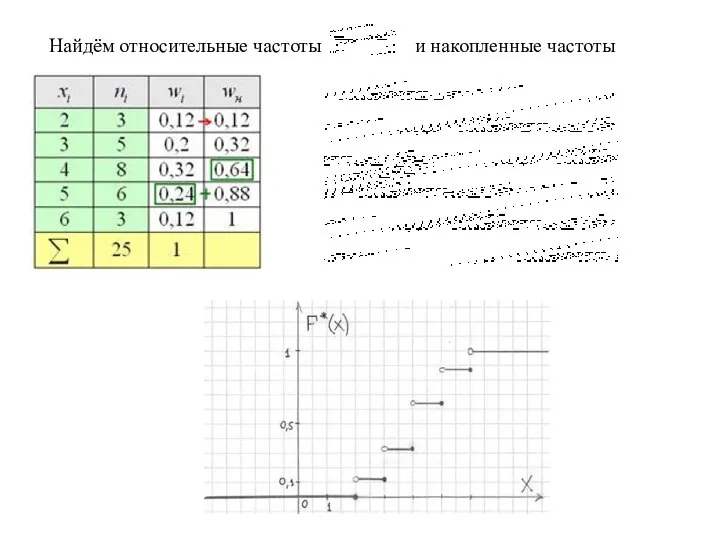
- 38. Найдём относительные частоты и накопленные частоты
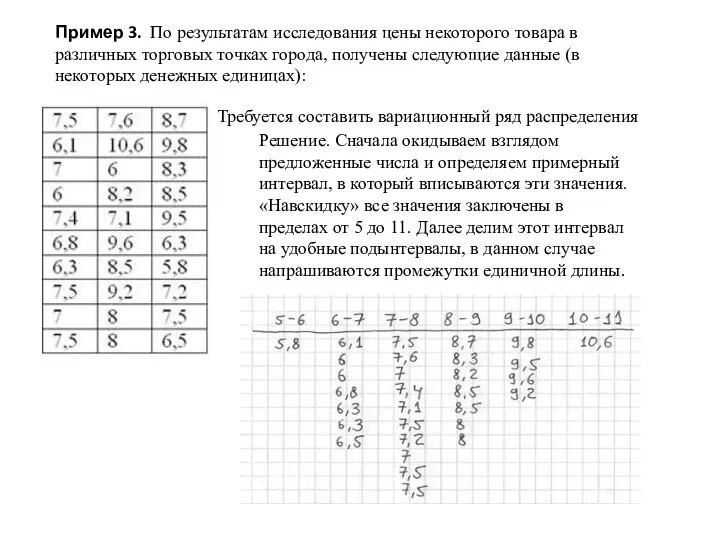
- 40. Пример 3. По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные
- 41. Вычислим размах вариаци: Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на
- 42. Убеждаемся в том, что самая большая варианта 10,6 вписалась в последний частичный интервал и отстоит от
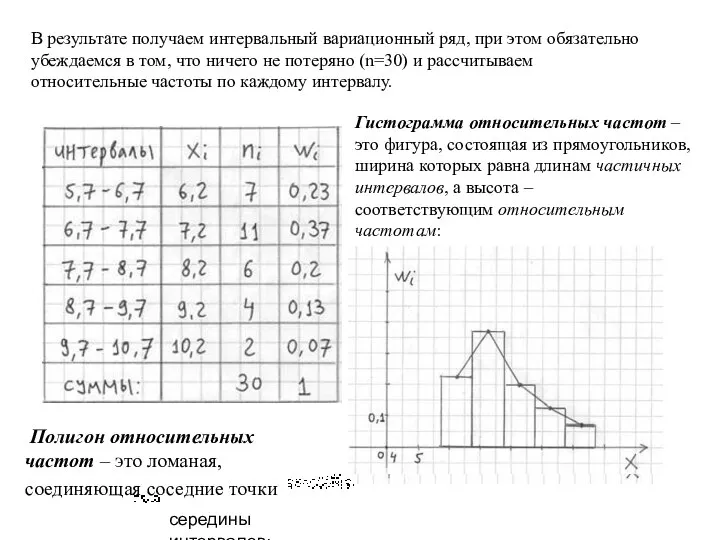
- 43. В результате получаем интервальный вариационный ряд, при этом обязательно убеждаемся в том, что ничего не потеряно
- 46. Скачать презентацию



































 Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Тригонометрия. Учебно-игровое пособие
Тригонометрия. Учебно-игровое пособие Дискретные случайные величины
Дискретные случайные величины Геометрия в искусстве
Геометрия в искусстве Математический диктант выражениями в тетрадь
Математический диктант выражениями в тетрадь СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Статистическая обработка измерений
Статистическая обработка измерений Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки График функции y = kf (x)
График функции y = kf (x) Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Равенство векторов
Равенство векторов Математика ЕГЭ. Первое занятие
Математика ЕГЭ. Первое занятие Метод Крамера
Метод Крамера Определенный интеграл. Формула Ньютона - Лейбница
Определенный интеграл. Формула Ньютона - Лейбница Деление круга на 2, 4, 8 частей
Деление круга на 2, 4, 8 частей Организация коррекционной работы по математике
Организация коррекционной работы по математике Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Пирамида. Египетские пирамиды
Пирамида. Египетские пирамиды Числовое и буквенное выражения
Числовое и буквенное выражения Игровые моменты
Игровые моменты Переместительное свойство умножения
Переместительное свойство умножения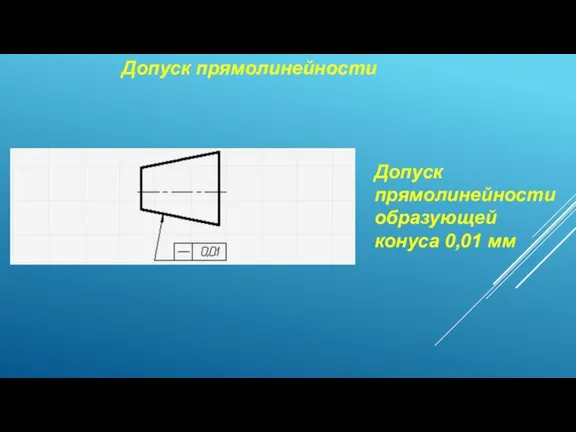 Допуск прямолинейности
Допуск прямолинейности Презентация на тему Сложение чисел с разными знаками
Презентация на тему Сложение чисел с разными знаками  Презентация на тему Перпендикулярность
Презентация на тему Перпендикулярность  Состав числа (домики)
Состав числа (домики) Элементы комбинаторики. Лекция 111
Элементы комбинаторики. Лекция 111