Средние величины. (Лекция 4.1)

Категория средней величины имеет одну из самых древних историй. Теоретическое осмысление средних можно найти в трудах античных философов. В произведениях Аристотеля, Гераклита, Архимеда, Пифагора и других содержится понимание средней как равнодействующей всех определенных условий, которые учавствуют в образовании рассматриваемой совокупности индивидуальных величин.
В.Петти (1623-1687 гг.)
А.Кетле (1796-1874 гг.)

Главное значение средних состоит в их обобщающей функции, т.е. в замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя отражает совокупный результат развития и является равнодействующей различных причин и сил, воздействующих на эти явления.

Использование средних величин предполагает следование определенным правилам.
1. До вычисления средних необходимо обеспечить качественную однородность совокупность.
2. Средние величины вычисляются по массовым данным, т.е. по данным достаточно большого числа единиц наблюдения.
3. Нельзя ограничиваться вычислением средней в целом по совокупности, не меньшее значение имеют средние характеристики и для каждого отдельного типа.

Пример 1. Даны сведения о заработной плате шести работников (в условных единицах) – 90, 120, 108, 206, 160, 184. Определить средний размер заработной платы данной совокупности работников.

Если изучаемая совокупность велика, исходная информация чаще всего представлена группировкой, где значения усредняемого признака встречаются по нескольку раз и частота их различна. Это значит, что любая варианта этого признака оказывает неодинаковое влияние на среднюю величину, которая должна представлять собой результат равномерного распределения значений признака.

Пример 2. Распределение футбольных матчей высшей лиги России по числу забитых мячей за игру в 1992 г.

Если в группировке значения усредняемого признака заданы интервальным рядом, то при исчислении средней арифметической в качестве значения признака берутся середины интервалов. Условно предполагается, что единицы совокупности распределены равномерно по интервалу.
Для открытых интервалов значения признака определяются экспертным путем, качественным анализом, исходя из сущности и свойств природы признака. Можно также использовать формальный способ прибавления единицы к максимальному определенному значению и вычитания единицы из минимального заданного значения признака.

Пример 3. Распределение рабочих N-ского предприятия по возрасту.

Пример 4.
Известно, что с площади 145 десятин собран урожай в 2595,5 т какой-то продукции. Отношение тонн (средняя урожайность данной культуры с одной десятины). Этот вид средней называется в статистике неявной формой средней.

Мода (Мо).
- представляет наиболее часто встречающееся значение признака в упорядоченной совокупности, наиболее типичное среднее. В дискретном ряду Мо определяется без вычислений как значение признака с наибольшей частотой. (См. пример 2.)
Если в вариационном ряду (в группировке) равная максимальная частота встречается у двух или нескольких значений признака, то он считается бимодальным или мультимодальным. Это говорит о неоднородности совокупности и, следовательно, надо проверить правильно ли составлена группировка.

Для вычисления моды в интервальном ряду сначала определяется класс, т.е. интервал с наибольшей частотой. Затем МО вычисляется по формуле: , где
X0 – нижняя граница модально интервала;
К – величина интервала;
P1 – частота интервала предшествующая модальному;
P2 - частота модально интервала;
P3 - частота интервала, последующего за модальным.

Вычислим МО по данным примера 3.
Получается, что наиболее типичный возраст рассматриваемой группы рабочих – 26, 15 лет. Этот возраст наиболее часто встречается в данной группе рабочих.

Приближенное значение моды можно определить по графику. Для этого надо построить гистограмму распределения.
Рис.1. Гистограмма распределения рабочих N-ского предприятия по возрасту.

Графическое определение моды применяется во всех случаях, когда в задачу исследования не входит обязательно получение точного значения наиболее распространенной величины признака. Например, для проверки рабочей гипотезы, когда точная величина принципиальной роли не играет, или для повышения наглядности материала. По нескольким графикам можно провести приблизительное сравнение мод различных признаков, чего невозможно сделать по таблицам.

Медиана (Ме)
- величина, определяющая значение признака, находящегося в середине упорядоченной совокупности. Медиана делит изучаемую совокупность так, что число единиц с большим и меньшим, чем медиана значением признака, одинаково.

Чтобы определить Ме в дискретном ряду, надо построить ряд накопленных частот, затем поделить сумму всех частот пополам, а затем по накопленным частотам определить величину варианты, соответстующей той группе, в которой накопленная частота впервые превышает половину общей численности совокупности. В примере 2 ряд накопленных частот будет выглядеть так: 21, 62, 104, 141, 160, 170, 176, 179. Полусумма всех этих частот равна 179/2=89,5. Эта величина входит в третью группу из накопленных частот, т.е. в данном примере третья из накопленных частот своей величиной превысила значение полусуммы всех частот. Следовательно медиана равна 2.

В интервальной группировке для вычисления Ме необходимо найти медианный интервал – интервал, которому соответствует первая из накопленных частот, превышающая половину суммы всех частот ряда распределения. Затем считают по формуле:
X0 – нижняя граница медианного интервала;
K – величина медианного интервала;
∑m-1 – сумма частот интервалов, предшествующих медианному;
Pm – частота медианного интервала;
∑Р – сумма частот. Pm

Определим Ме по данным примера 3. Ряд накопленных частот принимает следующий вид: 48; 168;243; 305; 359. Полусумма частот равна 359/2=179,5. Полученные данные говорят о том, что медианным является третий интервал, т.е. интервал «30-40».
Величина Ме свидетельствует, что половина рабочих рассматриваемой группы имеет средний возраст 31,53 года.

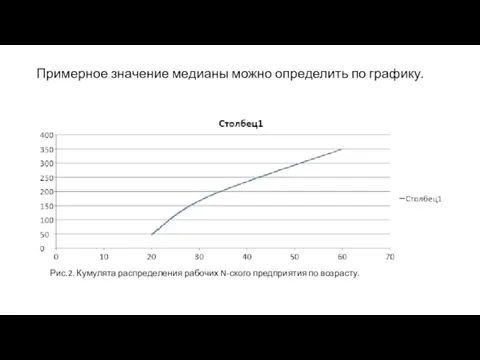
Примерное значение медианы можно определить по графику.
Рис.2. Кумулята распределения рабочих N-ского предприятия по возрасту.

Обобщая три средние величины, расчитанные по одним и тем же данным, видим существующую разницу. Средний возраст условной группы рабочих – 33,6 лет, наиболее распространенный, часто встречающийся средний возраст (Мо) – 26,2 лет, при этом половина рассматриваемой группы имеет средний возраст (Ме) – 31,5 лет. Какой величине следует отдать предпочтение? Какой показатель считать наиболее достоверным и точным?

При решении этих вопросов надо помнить:
1. Мода (Мо) имеет значение в том случае, когда её величина расходится и с медианой (Ме), и со средней арифметической ( ), им не следует пренебрегать. Это же можно сказать и о медиане. Так что для исследования полезно вычислять все три показателя.
2. Различие в значении величин обусловлено ассиметрическим распределением. Средняя арифметическая подвержена влиянию каждой варианты, поэтому она смещается в направлении наибольших значений признака. На моду (максимальные и минимальные) варианты влияния не оказывают. Медиана зависит только от числа вариант, а не от их величины.

3. Медиана по своей математико-статистической природе является самой представительной средней. При больших колебаниях в значениях признаков или когда не определены крайние интервалы в группировках, лучше пользоваться медианой. При вычислении моды для интервальной группировки желательно, чтобы интервалы были равновеликими.
4. Мода чаще других величин применяется по отношению к качественным признакам. Если скопление частот возле моды составляет 10-15 % их общего числа, особое значение приобретает медиана, представляя более достоверное значение среднего показателя.

Спасибо за внимание!