Содержание
- 2. План. 1. Первообразная. Правила отыскания первообразных. 2. Неопределенный интеграл. Правила интегрирования. 3. Понятие определенного интеграла. Формула
- 3. Опр 1. Функцию у = F(х) называют первообразной для функции у = f(x) на заданном промежутке
- 4. Таблица первообразных.
- 5. Правила отыскания первообразных. Правило 1. Первообразная суммы равна сумме первообразных. Y= F(х) + G(х) Правило 2.
- 6. ПРИМЕРЫ. Пример 1. Найти первообразную для функции у = 2х + соsх. Первообразной для 2x служит
- 7. 3.2. Неопределенный интеграл. Правила интегрирования. Теорема. Если у = F(х) — первообразная для функции у =
- 8. Таблица основных неопределенных интегралов.
- 9. Правила интегрирования. Правило 1. Интеграл от суммы функций равен сумме интегралов этих функций: Правило 2. Постоянный
- 15. Скачать презентацию












 Урок математики в 1 классе
Урок математики в 1 классе Буквенные выражения
Буквенные выражения Дискретное преобразование Фурье (окончание)
Дискретное преобразование Фурье (окончание) Третий признак подобия треугольников
Третий признак подобия треугольников Линейная регрессия
Линейная регрессия Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Сфера и плоскость
Сфера и плоскость Уравнение. Корень уравнения
Уравнение. Корень уравнения Степень с натуральным показателем и ее свойства. Обобщение. 7 класс
Степень с натуральным показателем и ее свойства. Обобщение. 7 класс Противоположные числа. Устный счет
Противоположные числа. Устный счет Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Справочный материал. 9 класс
Справочный материал. 9 класс Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число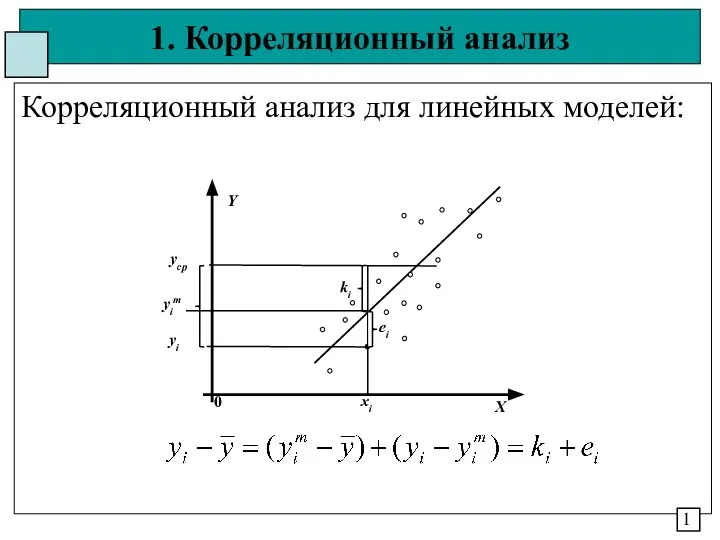 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Подготовка к ГИА по математике. Задания 6
Подготовка к ГИА по математике. Задания 6 Презентация на тему О числах
Презентация на тему О числах  Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Построение диаграмм и графиков
Построение диаграмм и графиков Тесты по математике
Тесты по математике Геометрическая прогрессия
Геометрическая прогрессия Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Сумма углов треугольника
Сумма углов треугольника Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Линии на плоскости
Линии на плоскости