Содержание
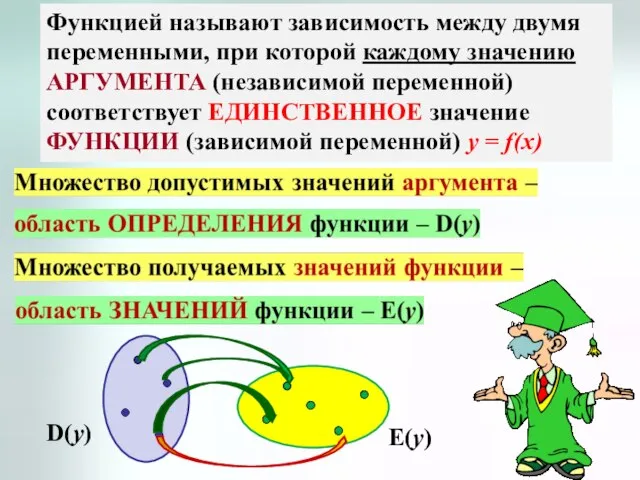
- 2. Функцией называют зависимость между двумя переменными, при которой каждому значению АРГУМЕНТА (независимой переменной) соответствует ЕДИНСТВЕННОЕ значение
- 3. Способы задания функции Аналитический (формула) Табличный (в виде таблицы) Графический (график) Описательный (соответствие множеств)
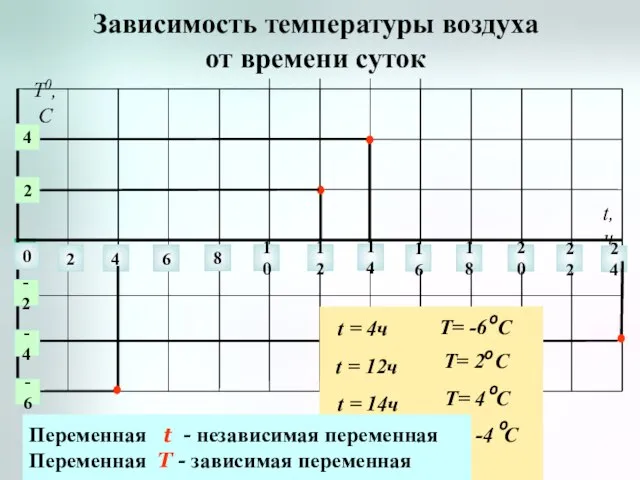
- 4. Зависимость температуры воздуха от времени суток 0 2 4 6 8 10 12 14 22 24
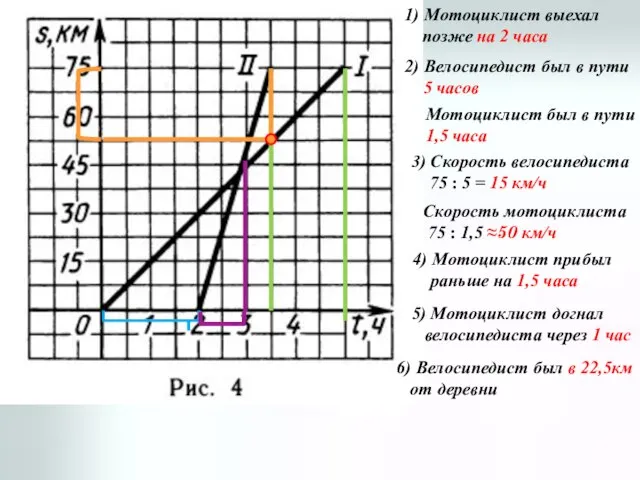
- 5. 1) Мотоциклист выехал позже на 2 часа 2) Велосипедист был в пути 5 часов Мотоциклист был
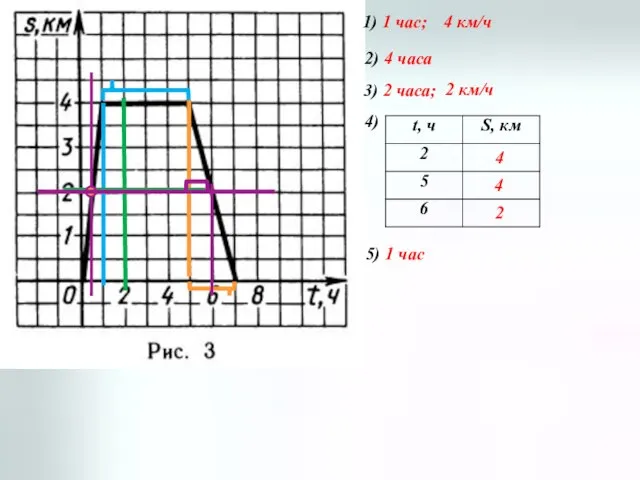
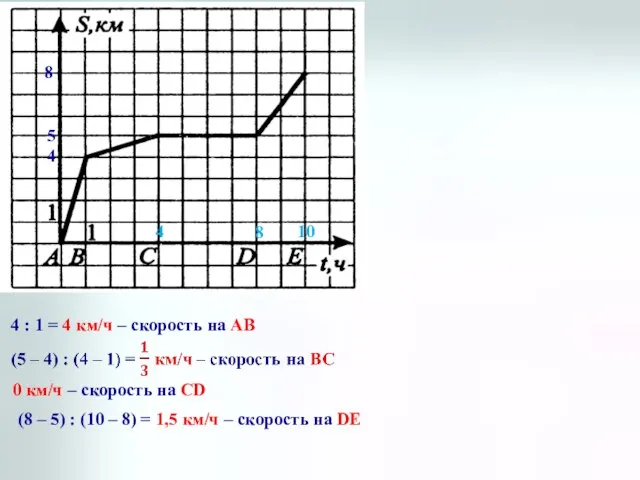
- 6. 1) 1 час; 4 км/ч 2) 4 часа 3) 2 часа; 2 км/ч 4) 4 4
- 7. 4 5 8 4 8 10 4 : 1 = 4 км/ч – скорость на АВ
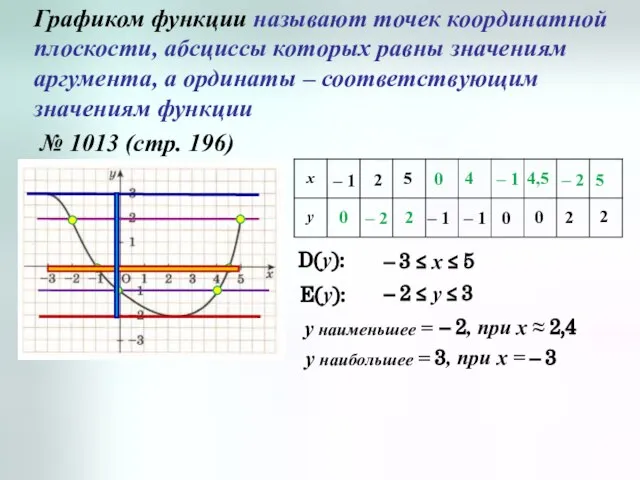
- 8. Графиком функции называют точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям
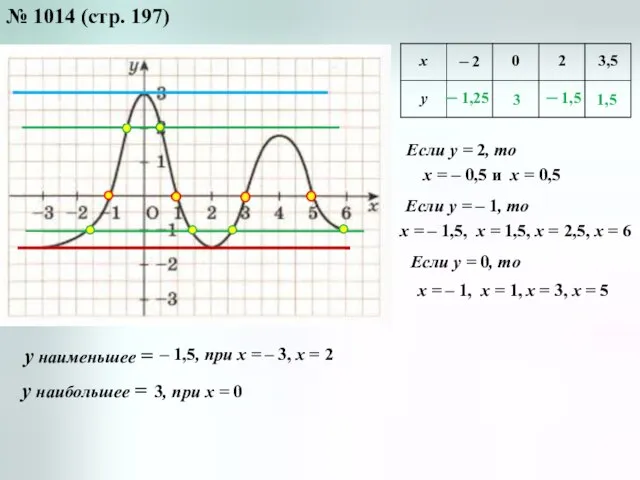
- 9. Если у = 0, то Если у = – 1, то Если у = 2, то
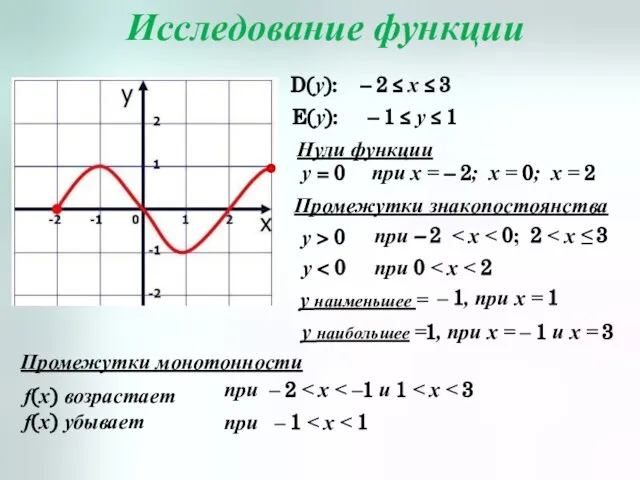
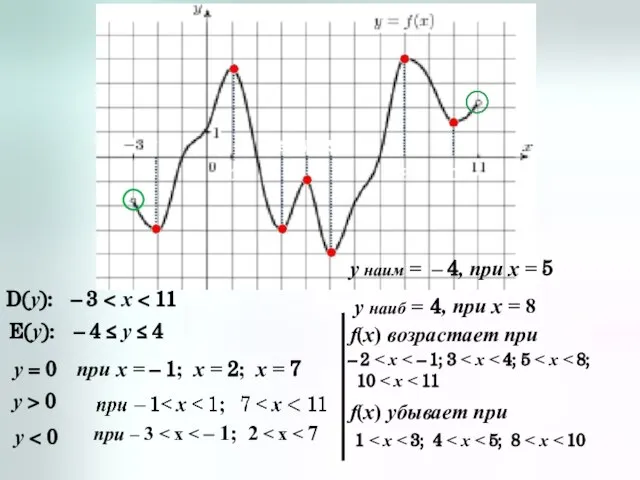
- 10. Исследование функции D(y): E(y): – 2 ≤ x ≤ 3 – 1 ≤ y ≤ 1
- 11. D(y): E(y): – 3 – 4 ≤ y ≤ 4 y = 0 при х =
- 12. Решите задачу, составив уравнение. Некоторое расстояние автобус проехал за 4 ч, а автомобиль - за 3
- 14. Скачать презентацию


 Линейные алгоритмы
Линейные алгоритмы Многочлены. Задания
Многочлены. Задания Решение интеграла
Решение интеграла Пример проектирования цифрового устройства
Пример проектирования цифрового устройства Дроби
Дроби Аксиомы стереометрии
Аксиомы стереометрии Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Задача
Задача Задача про комбинацию окружностей и квадрата и её обобщение от Тимофея Гаврикова
Задача про комбинацию окружностей и квадрата и её обобщение от Тимофея Гаврикова Показательные уравнения: типы и методы решения
Показательные уравнения: типы и методы решения Устное решение квадратных уравнений
Устное решение квадратных уравнений Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе
Аттестационная работа. Исследовательская деятельность на уроках математики в 5 классе Сводка и группировка статистических данных
Сводка и группировка статистических данных Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Нелинейное программирование
Нелинейное программирование Эконометрка ва омори риёзи
Эконометрка ва омори риёзи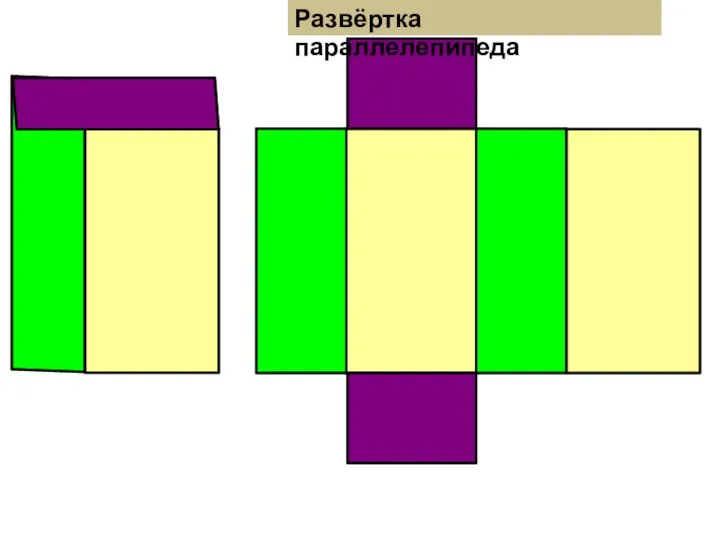 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Сложение и вычитание трёхзначных чисел
Сложение и вычитание трёхзначных чисел Теорема Пифагора. Деление дробей
Теорема Пифагора. Деление дробей Тригонометрия в различных областях науки и жизни
Тригонометрия в различных областях науки и жизни Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Виды векторов
Виды векторов KomplanarnVektor
KomplanarnVektor Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Логарифмические уравнения
Логарифмические уравнения Почему нельзя делить на ноль
Почему нельзя делить на ноль Задачи на построение (геометрия, 7 класс)
Задачи на построение (геометрия, 7 класс) Решение задач на проценты
Решение задач на проценты