Содержание
- 2. Пример. Самостоятельно: вычислить указанный предел; Самостоятельно: вычислить указанный предел; привести еще 2 аналогичных примера.
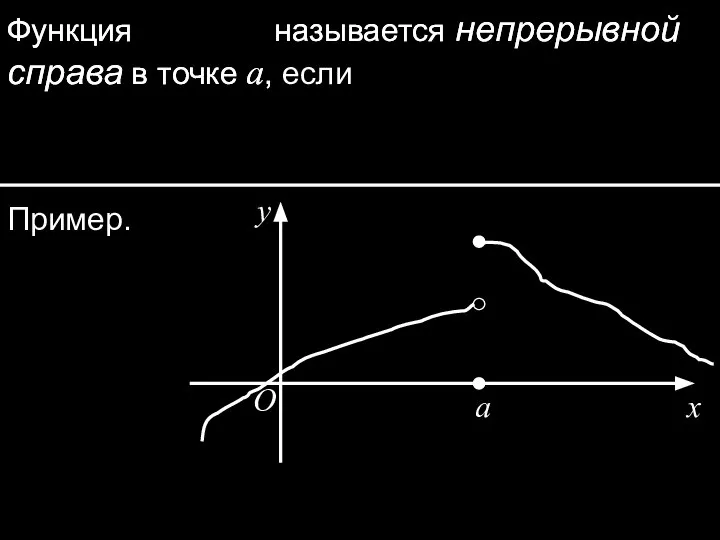
- 3. Функция называется непрерывной справа в точке a, Функция называется непрерывной справа в точке a, если Пример.
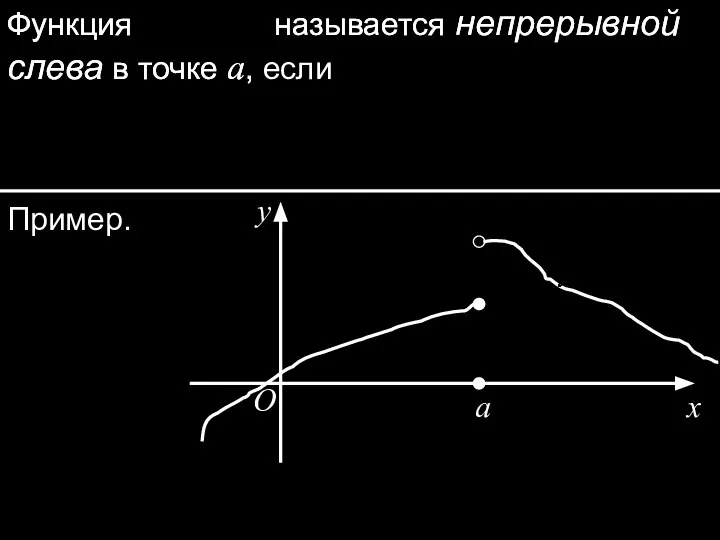
- 4. Функция называется непрерывной слева в точке a, Функция называется непрерывной слева в точке a, если Пример.
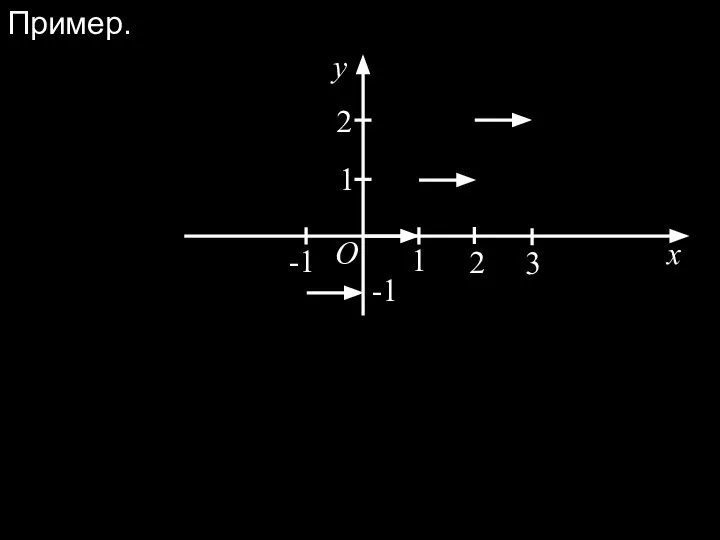
- 5. Пример. x O y 1 1 2 2 3 -1 -1
- 6. Теорема 1. Теорема 1. Для того, чтобы функция f была непрерывной в точке a Теорема 1.
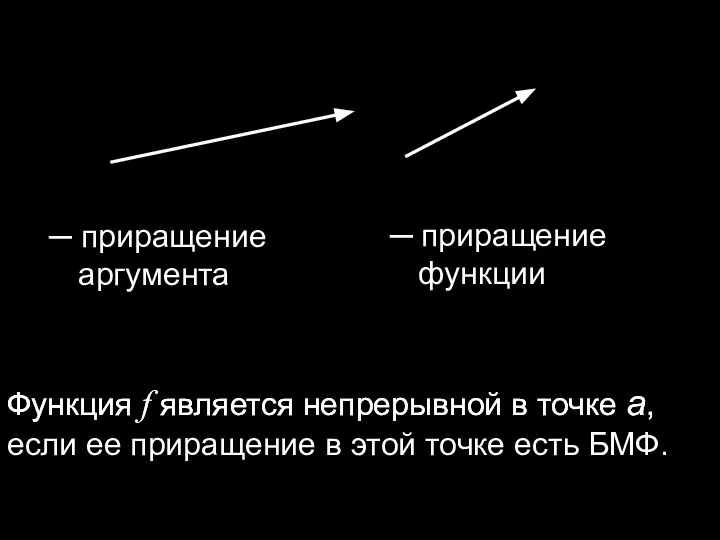
- 7. ─ приращение аргумента ─ приращение функции Функция f является непрерывной в точке а, Функция f является
- 8. Теорема 2. (Алгебраические свойства непрерывных функций) Пусть функции и непрерывны в точке a. Тогда, функции также
- 9. Теорема 3. (О непрерывности сложной функции) Пусть функция непрерывна в точке функция непрерывна в точке Тогда,
- 10. Теорема 4. (О непрерывности обратной функции) Пусть функция непрерывна в точке Тогда, если для функции f
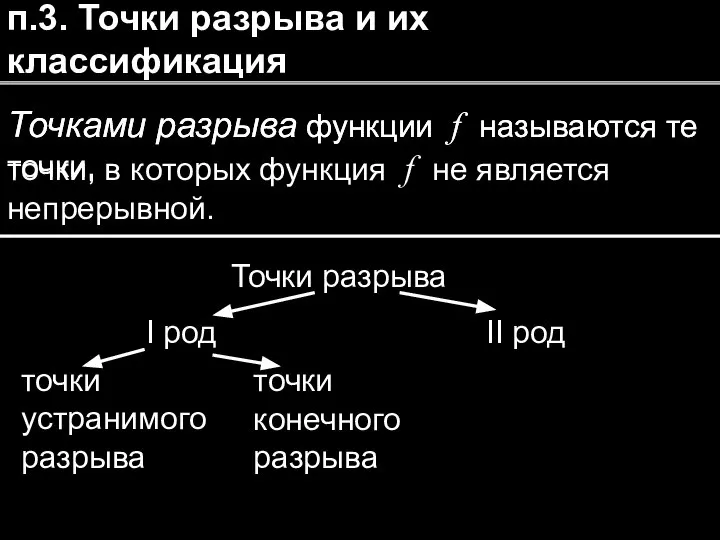
- 11. п.3. Точки разрыва и их классификация Точками разрыва функции f называются те точки, Точками разрыва функции
- 12. Точка называется точкой разрыва I рода функции , Точка называется точкой разрыва I рода функции ,
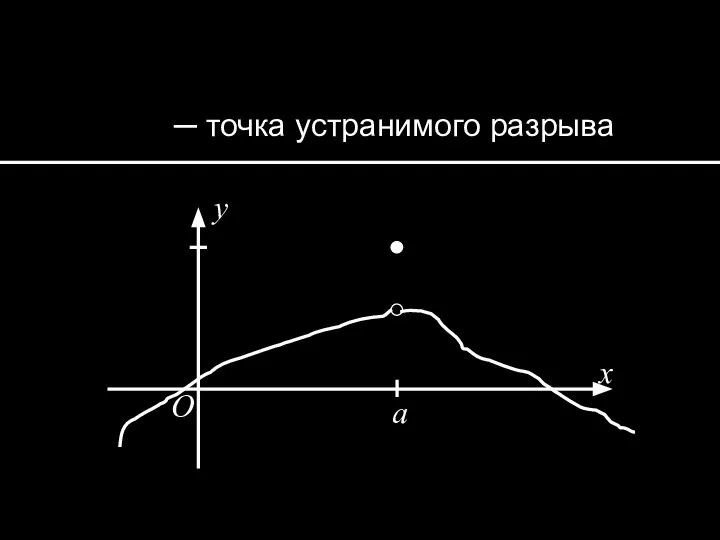
- 13. ─ точка устранимого разрыва x y O a
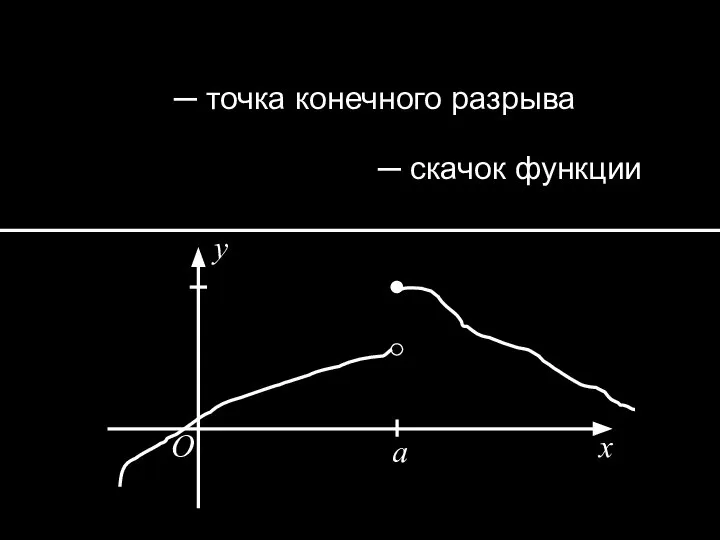
- 14. ─ точка конечного разрыва x y O a ─ скачок функции
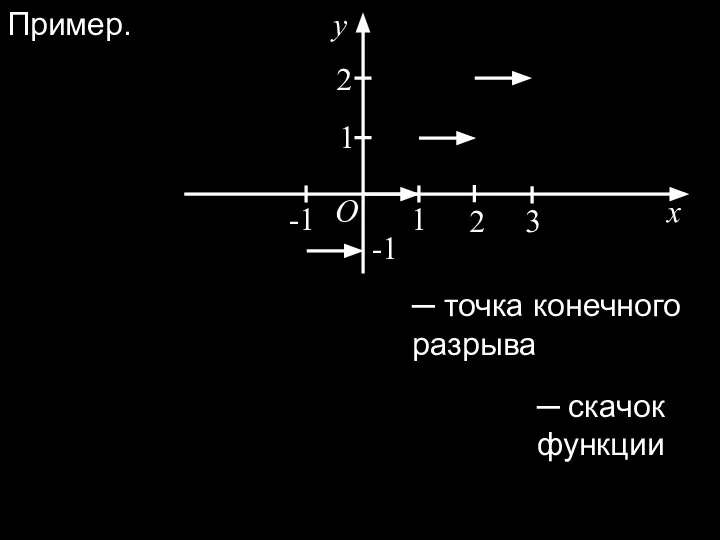
- 15. Пример. x O y 1 1 2 2 3 -1 -1 ─ точка конечного разрыва ─
- 16. Точка называется точкой разрыва II рода функции , Точка называется точкой разрыва II рода функции ,
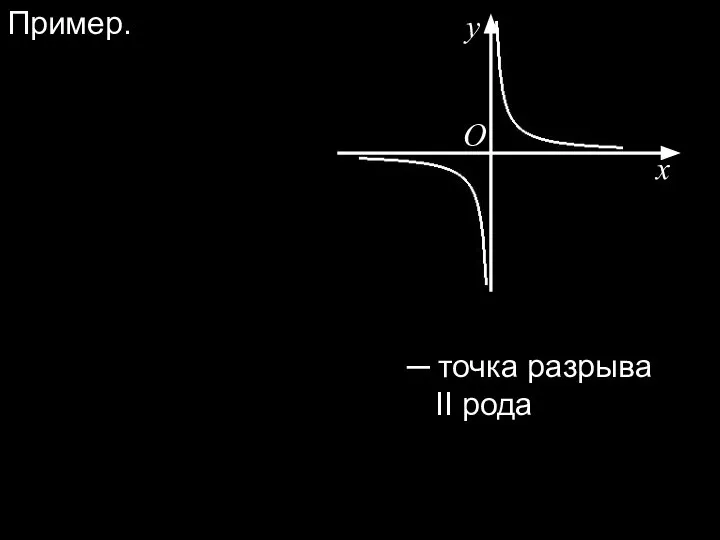
- 17. Пример. x O y ─ точка разрыва II рода
- 18. Функция называется непрерывной на отрезке , если она непрерывна в каждой точке интервала , п.4. Основные
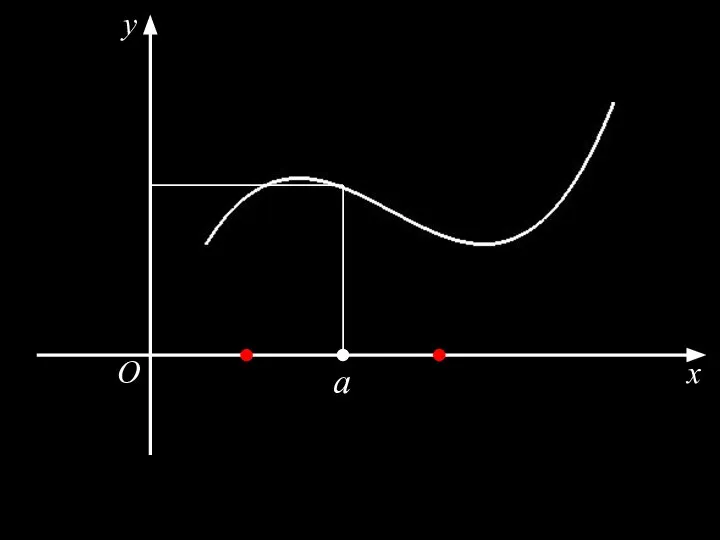
- 19. Теорема 5. (Об устойчивости знака) Пусть функция непрерывна в точке a и . и . Тогда
- 20. x O y a
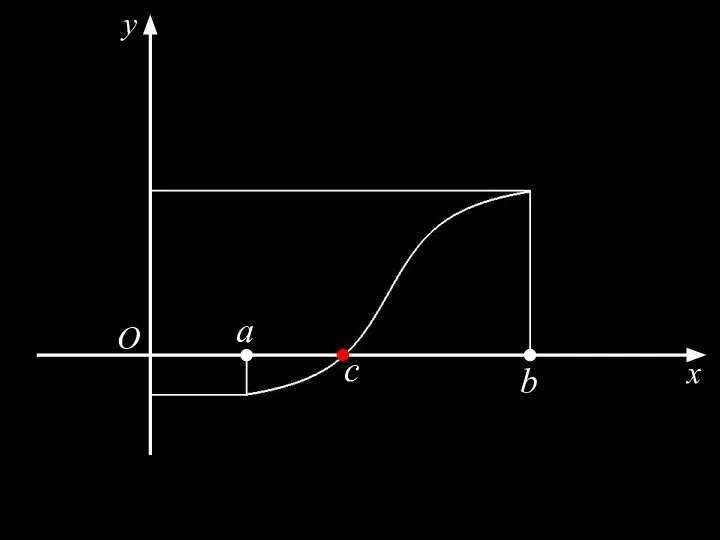
- 21. Теорема 6. (Первая теорема Больцано–Коши) Пусть функция непрерывна на отрезке на концах отрезка принимает значения разных
- 22. x O y a b c
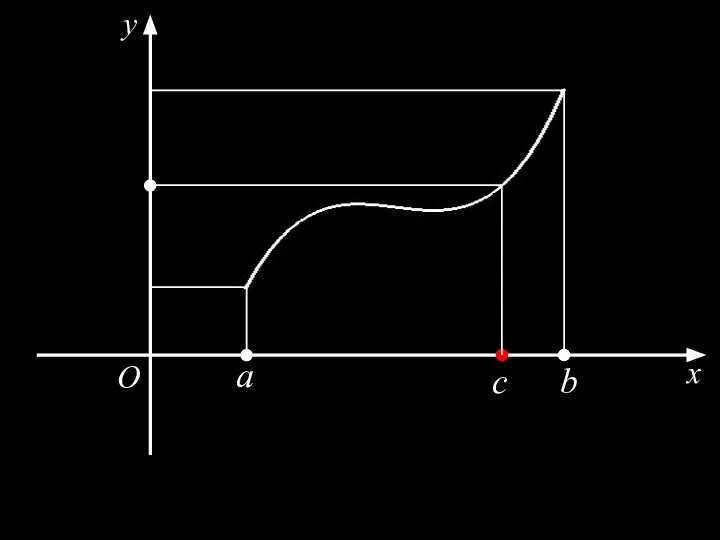
- 23. Теорема 7. (Вторая теорема Больцано–Коши) Пусть функция непрерывна на отрезке Тогда
- 24. x O y a b c
- 25. Теорема 8. (Первая теорема Вейерштрасса) Пусть функция непрерывна на отрезке Тогда она ограничена на этом отрезке.
- 27. Скачать презентацию












 Задача на знаходження суми
Задача на знаходження суми Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Решение задач с параметрами
Решение задач с параметрами Умножение матрицы на число
Умножение матрицы на число Правила нахождения производных
Правила нахождения производных Сфера
Сфера krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Контрольная работа по алгебре
Контрольная работа по алгебре Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Измеряй и сравнивай
Измеряй и сравнивай Прибавить и вычесть 2
Прибавить и вычесть 2 Признак перпендикулярности прямой и плоскости. 10 класс
Признак перпендикулярности прямой и плоскости. 10 класс Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Повторение: Числа
Повторение: Числа Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Её величество Степень
Её величество Степень Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Векторы в пространстве. Решение задач по готовым чертежам
Векторы в пространстве. Решение задач по готовым чертежам Теоремы Пифагора
Теоремы Пифагора Задачи на проценты
Задачи на проценты Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс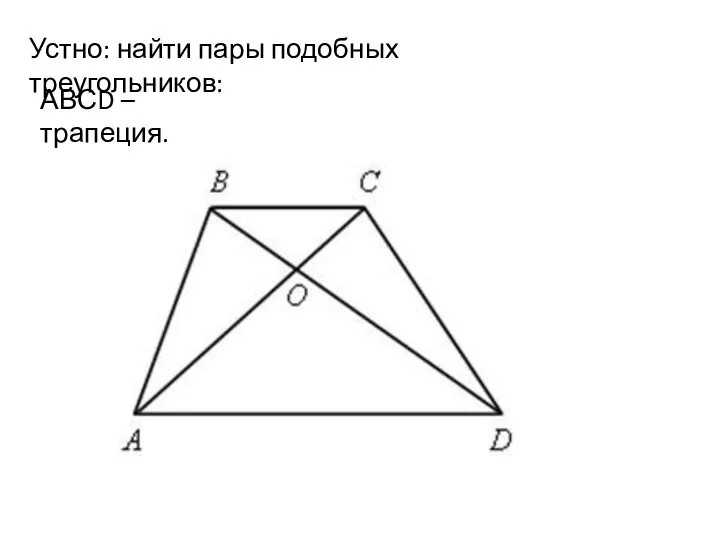 Признак подобия треугольников. Урок 32
Признак подобия треугольников. Урок 32 Теорема Пифагора
Теорема Пифагора Решение задач. Таблица умножения на 6. Кратное сравнение чисел
Решение задач. Таблица умножения на 6. Кратное сравнение чисел Простейшие комбинации
Простейшие комбинации