Содержание
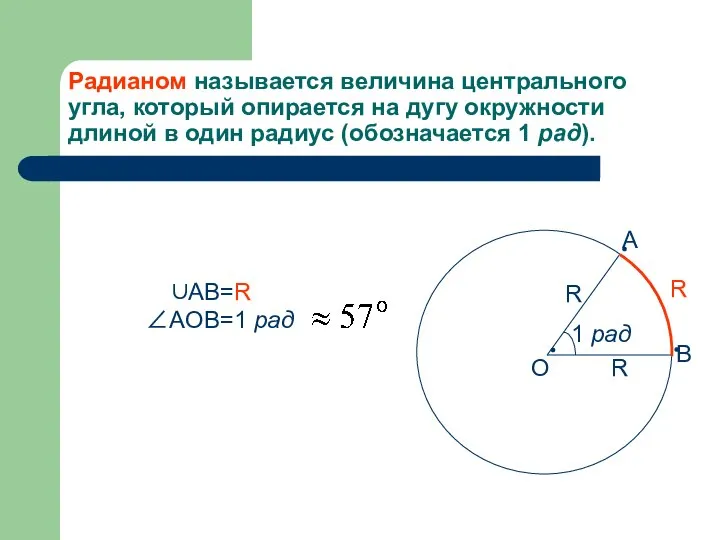
- 2. Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1
- 3. α0= α0· рад − правило перевода из градусной меры в радианную; Пример: α рад= α· −
- 4. Основные углы ( ВЫУЧИТЬ !)
- 5. 150о 135о 120о Найти градусную меру угла, выраженного в радианах:
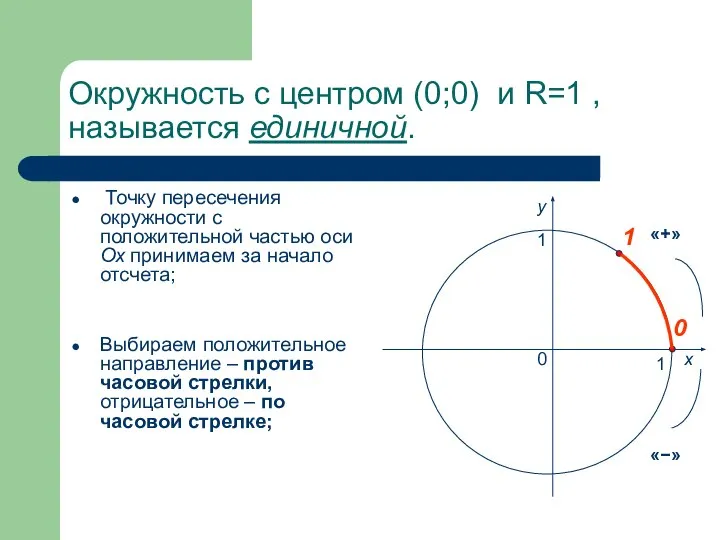
- 6. Окружность с центром (0;0) и R=1 , называется единичной. Точку пересечения окружности с положительной частью оси
- 7. Напомним, что декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и
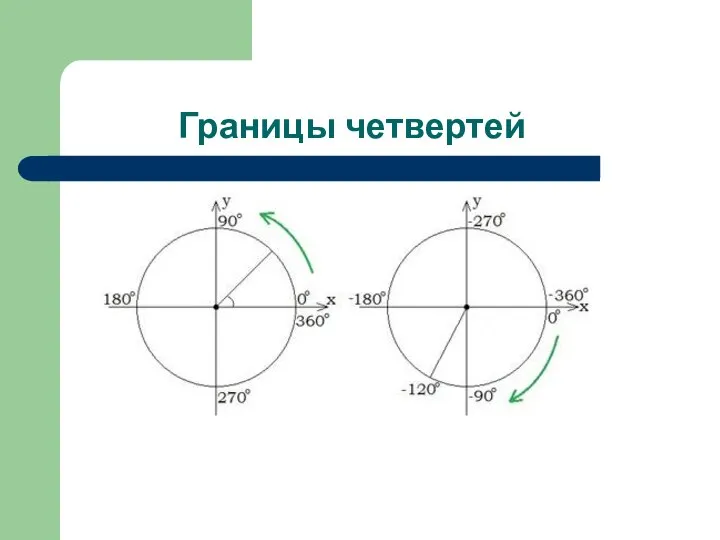
- 8. Границы четвертей
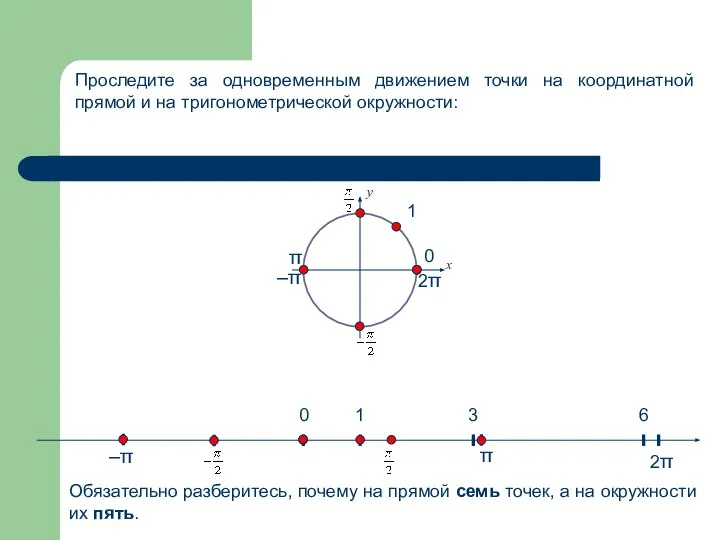
- 9. 0 1 0 3 2π 6 π π 2π у х 1 –π –π Проследите за
- 10. В какой четверти находится угол:
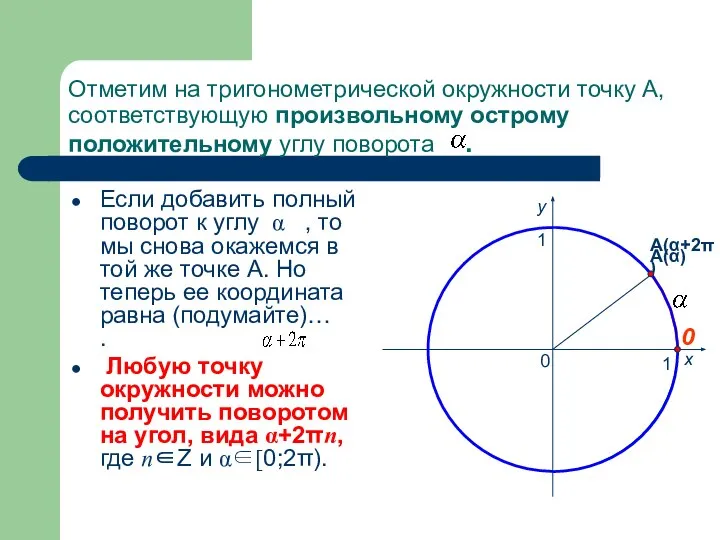
- 11. Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному углу поворота . Если добавить полный
- 12. В какой четверти углы: 790 0 = 360 . 2 + 70 = 700 - Iч
- 14. Скачать презентацию






 Домашнее задание. Решение задач
Домашнее задание. Решение задач Векторы на плоскости
Векторы на плоскости Случаи вычитания 11-
Случаи вычитания 11- Знакомство с основными понятиями в математике. Задачи с несколькими вопросами
Знакомство с основными понятиями в математике. Задачи с несколькими вопросами Древнекитайское доказательство
Древнекитайское доказательство Пределы
Пределы История теоремы Пифагора
История теоремы Пифагора Построение сечений многогранников
Построение сечений многогранников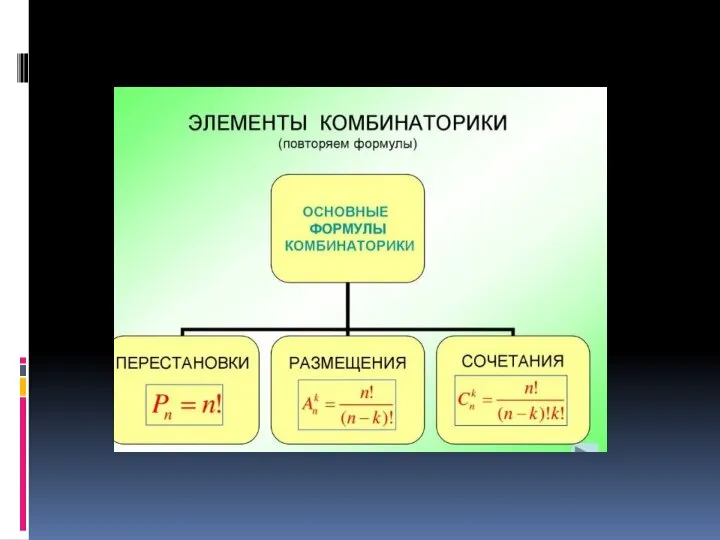 Основные понятия комбинаторики
Основные понятия комбинаторики предел_числ_посл
предел_числ_посл Стереометрия. Многогранники
Стереометрия. Многогранники Отношения и пропорции. Золотое сечение
Отношения и пропорции. Золотое сечение Площади и объемы
Площади и объемы Частные производные. Полный дифференциал функции
Частные производные. Полный дифференциал функции Многоугольники
Многоугольники Многочлены с несколькими переменными и их стандартный вид
Многочлены с несколькими переменными и их стандартный вид Кусочная функция
Кусочная функция Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Презентация на тему Слагаемое сумма
Презентация на тему Слагаемое сумма  Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация на тему Нумерация в пределах 1000
Презентация на тему Нумерация в пределах 1000  Призма. Понятие и чертёж
Призма. Понятие и чертёж 1_2_opredeliteli (1)
1_2_opredeliteli (1) Центральная симметрия
Центральная симметрия Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел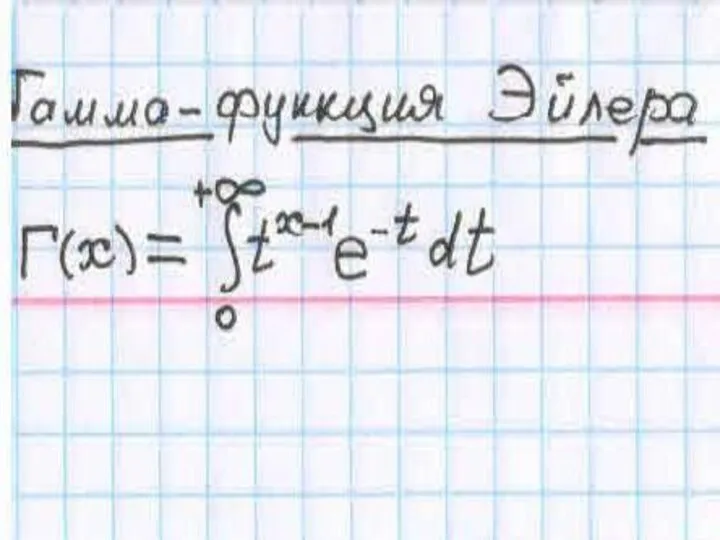 Гамма-функция Эйлера
Гамма-функция Эйлера