Содержание
- 2. Булева алгебра Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача –
- 3. Алгебра высказываний (логики) – математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
- 4. Сложные высказывания составляются из простых высказываний, соединенных логическими связками: «и», «или», «не» и т.д. 6 –
- 5. Отрицание (выражается словом «НЕ» Читается «неверно, что x») или инверсия. Обозначается чертой над высказыванием. Функция, реализующая
- 6. Конъюнкция (выражается словом «И») или логическое умножение (Читается «x и y») Обозначается *, ^, &(амперсенд). Функция,
- 7. Дизъюнкция (выражается словом «ИЛИ») логическое сложение (Читается «x или y») Обозначается +, v. Функция, реализующая эту
- 8. Импликация ( «если…то», «из…следует») Читается «из x следует y» или «если x, то y» Обозначается знаком
- 9. Эквиваленция (Читается «для того, чтобы x, необходимо и достаточно, чтобы y» или «x тогда и только
- 10. Алгебра логики используется при построении основных узлов ЭВМ. При изучении работы различных устройств компьютера приходится рассматривать
- 11. ПРИМЕР №1 Кол-во строк таблицы (кол-во сочетаний из 0 и 1) определяется по формуле 2п =22
- 12. ПРИМЕР №2 -Выполнить самостоятельно
- 13. Равносильные логические выражения Равносильные логические выражения - у которых последние столбцы таблиц истинности совпадают. Обозначают “=“.
- 14. Решение логических задач с помощью ТИ
- 15. Задание. Решить логическую задачу с помощью таблицы истинности На вопрос, кто из трёх учащихся изучал информатику,
- 17. Законы и тождества алгебры логики
- 21. Скачать презентацию

















 Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Решение задач разными арифметическими способами
Решение задач разными арифметическими способами Процент
Процент Нестандартные уравнения
Нестандартные уравнения Статистический анализ состава и использования фонда. Темпы роста фонда, числа читателей и книговыдачи
Статистический анализ состава и использования фонда. Темпы роста фонда, числа читателей и книговыдачи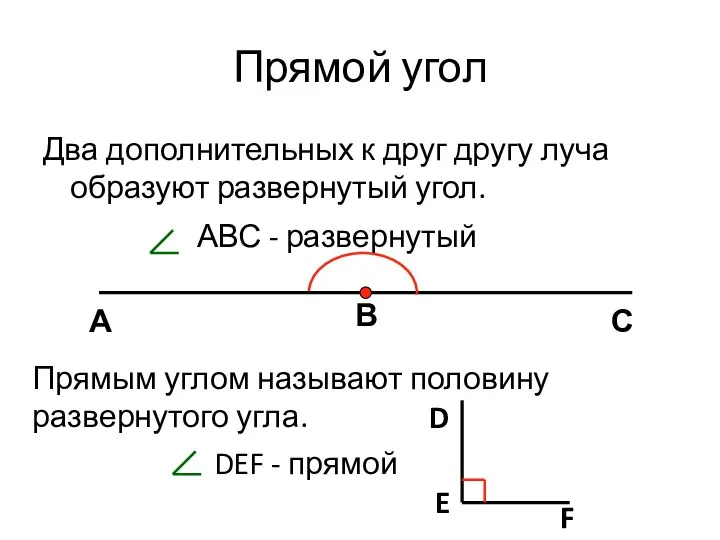 Прямой угол
Прямой угол Состав числа 10
Состав числа 10 Оригами в математике
Оригами в математике Вписанная и описанная окружности
Вписанная и описанная окружности Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Модели решения функциональных и вычислительных задач. Методы и технологии моделирования
Модели решения функциональных и вычислительных задач. Методы и технологии моделирования Завдання на відсотки
Завдання на відсотки Задачи на построение
Задачи на построение Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма Свойства числовых функций
Свойства числовых функций Упрощение выражений (5 лкасс)
Упрощение выражений (5 лкасс) Письменный прием вычитания
Письменный прием вычитания Устный счет
Устный счет Презентация на тему Устный счет по математике
Презентация на тему Устный счет по математике  Шар. Радиус. Центр
Шар. Радиус. Центр Математическая игра
Математическая игра Презентация на тему Виды движения
Презентация на тему Виды движения  Многогранники. Правильные многогранники
Многогранники. Правильные многогранники Числа от 1 до 10. Сложение и вычитание. Урок 2
Числа от 1 до 10. Сложение и вычитание. Урок 2 Элементы высшей математики
Элементы высшей математики Презентация на тему Числовые и алгебраические выражения
Презентация на тему Числовые и алгебраические выражения  Основные принципы комбинаторики
Основные принципы комбинаторики