797329 (1)

Урок № 1. Тема: «Развитие понятия о числе»
Талица 2020
Государственное автономное профессиональное образовательное учреждение Свердловской области «Талицкий лесотехнический колледж им. Н.И.Кузнецова
Выполнила преподаватель
Кудина Л.В.

Задание 1.Изучить материал.
Задание 2. Составить опорный (КРАТКИЙ!) конспект.
Задание 3.Выполнить практическую часть.
Задание 4.Используя Дополнительный материал №1 закрепить материал.
Задание 3 Отправить на проверку

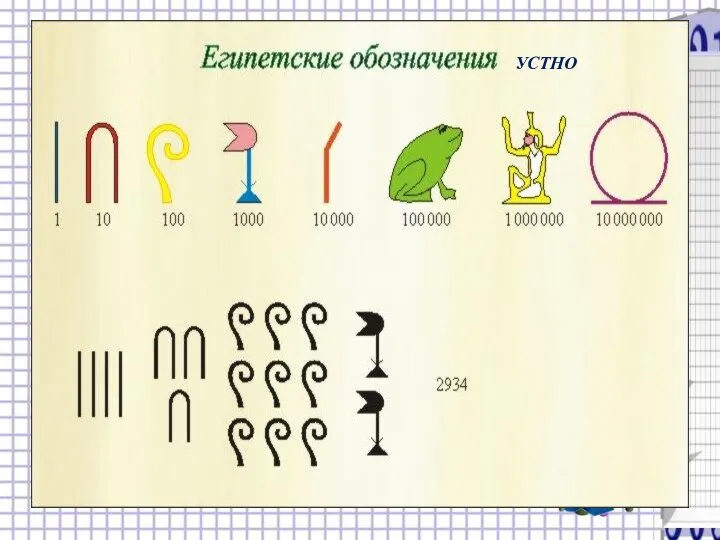
Из истории чисел
Возникнув еще в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось.
.
На первых этапах существования человеческого общества числа, открытые в процессе человеческой деятельности, служили для примитивного счета предметов, дней, шагов и т.п.
Число- основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций.
УСТНО

Из истории чисел
.
С развитием цивилизации ему потребовалось изобретать все большие и большие числа, уметь их записывать. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда
Потребовалась не одна сотня лет для того, чтобы математики смогли осмыслить понятие иррационального числа, и выработать способ записи такого числа и приближенного значения его в виде бесконечной десятичной дроби.
.Оно получило название мнимой единицы. После того как норвежский математик Гаспар Вессель (1745-1818) нашел возможность представить мнимое число геометрически, то так называемые «мнимые числа» получили свое место в множестве комплексных чисел.
УСТНО

Из истории чисел
.
.
Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали ¼, 1/8, …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, у них числитель всегда единица. Лишь значительно позже у греков, затем у индейцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В дальнейшем оказалось необходимым еще более расширить понятие числа. Последовательно появились числа иррациональные, отрицательные и комплексные.
УСТНО

Из истории чисел
.
.
Довольно поздно к семье чисел присоединился нуль. Первоначально слово нуль означало отсутствие числа(буквальный смысл латинского слова nullum –“ничего»). Действительно, если, например, от 3 отнять 3, тоне останется ничего. Для того, чтобы это «ничего» считать числом, появились основания лишь в связи с рассмотрением отрицательных чисел.
http://ppt-online.org/18501
УСТНО

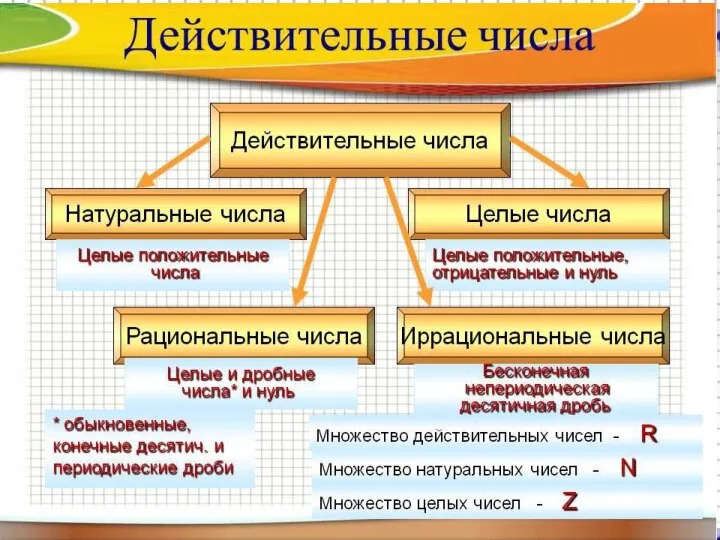
Натуральные числа
Натуральные числа (естественные числа) – числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Множество всех натуральных чисел принято обозначать знаком N. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
УСТНО

Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Сложение. Слагаемое + Слагаемое = Сумма
Умножение. Множитель * Множитель = Произведение
Возведение в степень , ab где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Вычитание. Уменьшаемое Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
Деление. Делимое / Делитель = (Частное, Остаток).
УСТНО

Целые числа – бывают положительными и отрицательными. Совокупность целых чисел образует множество целых чисел. Число вида а/в,
где а и b целые числа, причём
называется рациональным числом. Множество, состоящее из положительных и отрицательных дробных чисел, называется множеством рациональных чисел.
УСТНО

Основные свойства
Коммутативность сложения. A+B=B+A
Коммутативность умножения. A.B=B.A
Ассоциативность сложения. (A+B)+C=A+(B+C)
Ассоциативность умножения. (AB)C=A(BC)
Дистрибутивность умножения относительно
сложения.
УСТНО

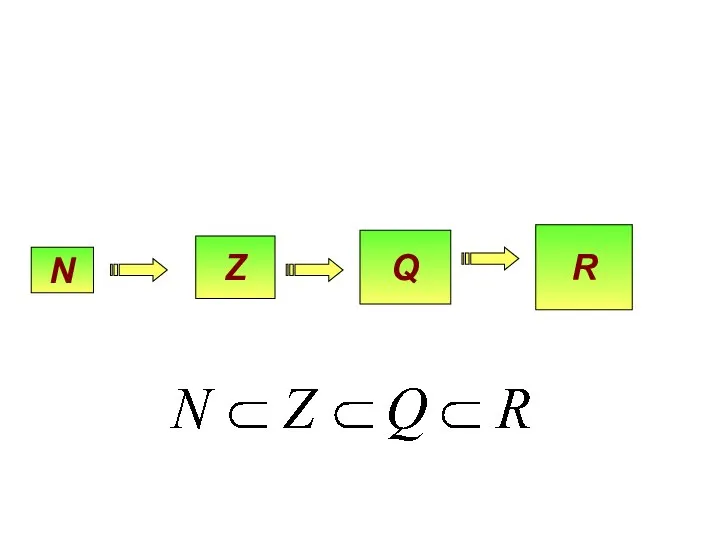
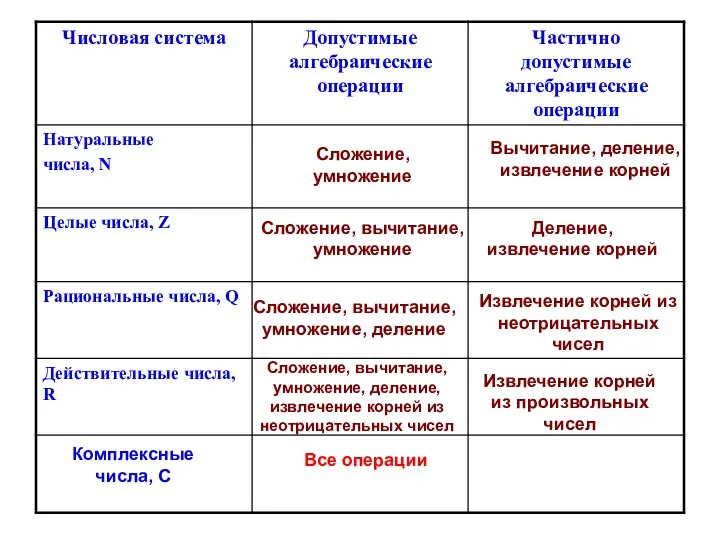
Числовые множества
УСТНО

УСТНО

Сложение, умножение
Вычитание, деление, извлечение корней
Сложение, вычитание, умножение
Деление, извлечение корней
Сложение, вычитание, умножение, деление
Извлечение корней из неотрицательных чисел
Сложение, вычитание, умножение, деление, извлечение корней из неотрицательных чисел
Извлечение корней из произвольных чисел
Комплексные числа, C
Все операции

Любое рациональное число можно представить либо в виде конечной десятичной дроби, либо в виде бесконечной периодической десятичной дроби.
Выполнить действия:
1.
2.
Письменно

Периодические дроби.
Определение: Периодические дроби бывают чистыми и смешанными.
Чистой периодической называется дробь, у которой период сразу после запятой.
.
Смешанной называется дробь, у которой между запятой и первым периодом есть одна или несколько повторяющихся цифр:
.
142857)
Письменно
Все определения выучить!!!

.
Обращение чистой периодической дроби в обыкновенную:
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно период сделать числителем, а в знаменателе написать цифру девять столько раз, сколько цифр в периоде.
О,(54)=54/99 =6/11
Письменно

.
Обращение смешанной периодической дроби в обыкновенную:
Чтобы обратить смешанную периодическую дробь в обыкновенную достаточно из числа стоящего до второго периода вычесть число стоящее до первого периода, и полученную разность взять числителем , а знаменателем написать цифру девять столько раз, сколько цифр в периоде, со столькими нулями сколько цифр между запятой и первым периодом:
Письменно

.
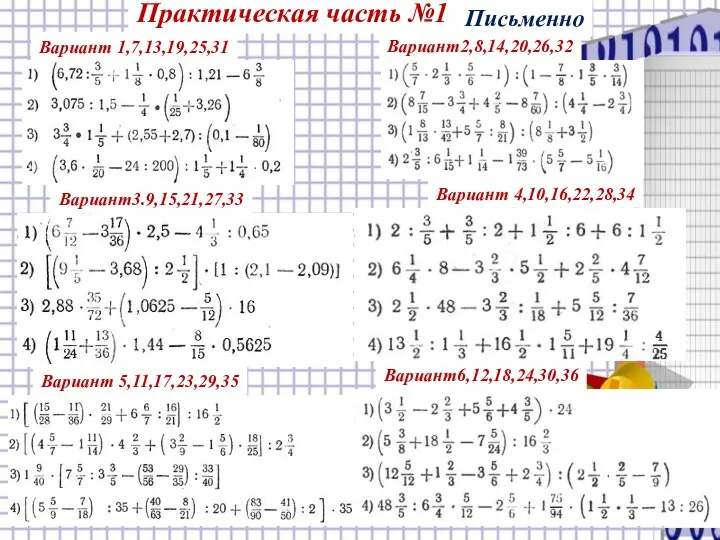
Вариант 1,7,13,19,25,31
Практическая часть №1
Вариант2,8,14,20,26,32
Вариант3.9,15,21,27,33
Вариант 4,10,16,22,28,34
Вариант 5,11,17,23,29,35
Вариант6,12,18,24,30,36
Письменно

Практическая часть №2 (смотри продолжение)
Письменно

Практическая часть №2 (продолжение)
Письменно

Действия над действительными числами
Дополнительный материал №1
Решите примеры, сверьтесь с ответами, при необходимости проведите работу над ошибками.
Дополнительный материал отправлять на проверку не надо

Обратите обыкновенные дроби в десятичные периодические:

Обратите чистые периодические десятичные дроби в обыкновенные:

Обратите смешанные периодические десятичные дроби в обыкновенные: