Слайд 2
Статистика
Задача 1.(Задача за първата контролна работа и Задача за изпита)
Чрез
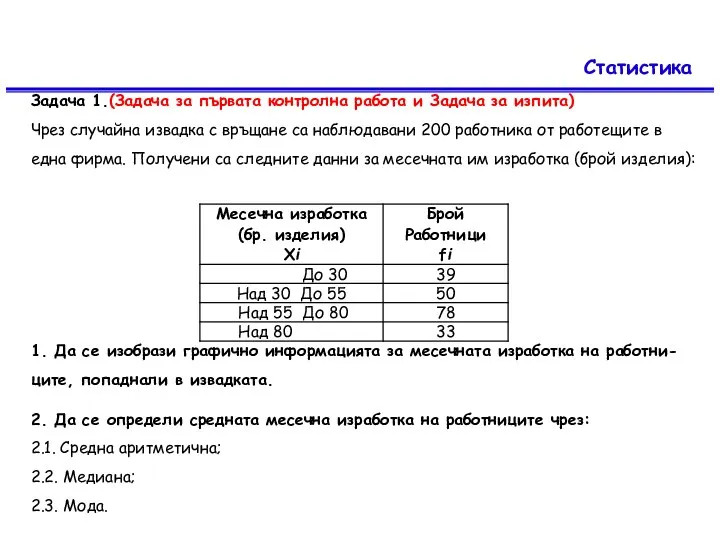
случайна извадка с връщане са наблюдавани 200 работника от работещите в една фирма. Получени са следните данни за месечната им изработка (брой изделия):
1. Да се изобрази графично информацията за месечната изработка на работни-ците, попаднали в извадката.
2. Да се определи средната месечна изработка на работниците чрез:
2.1. Средна аритметична;
2.2. Медиана;
2.3. Мода.
Слайд 3
Статистика
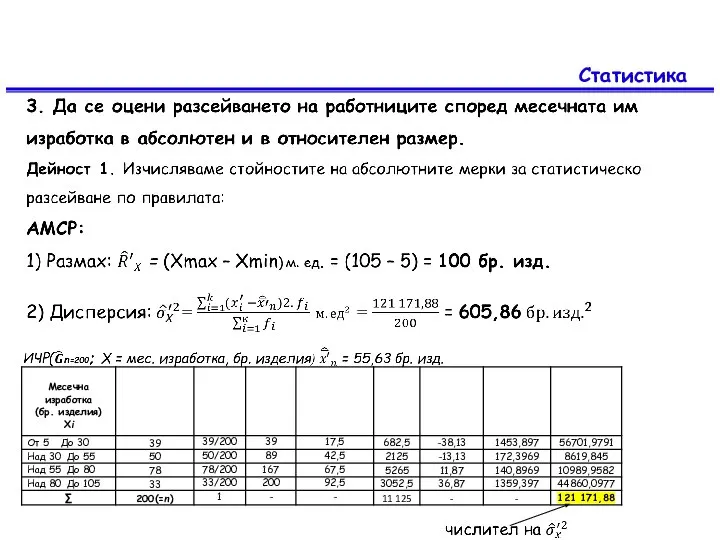
3. Да се оцени разсейването на работниците според месечната им изработка

в абсолютен и в относителен размер.
4. Да се определи интервалът на доверителност, в който се намира действител-ната средномесечна изработка на всичките работници от фирмата при гаран-ционна вероятност, равна на 95%.
5. Ще се измени ли обемът на извадката и как, ако при равни други условия се постави изискване точността на оценката на средната месечна изработка да се повиши три пъти?
Слайд 4
Статистика
Решение на задачата:
1. Да се изобрази графично информацията за месечната изработка

на работниците, попаднали в извадката.
Дейност 1. Ако в ИЧР има безкрайни интервали, то ние трябва да ги „затворим“, в смисъл – да обявим липсващата граница. Затваря-нето на такива интервали може да се извърши или по смисъл, или съвсем формално, като липсващите граници трябва да се изчислят така, че всички интервали да имат еднаква ширина l .
l = ? − ?, където: а – начало (ляв край на интервала); b – десен край на интервала.
l = 55 − 30 = 25 бр. изделия – ширина (дължина) на интервалите.
Слайд 5
Статистика
Началото на първия интервал ще определим, като от неговия край, в
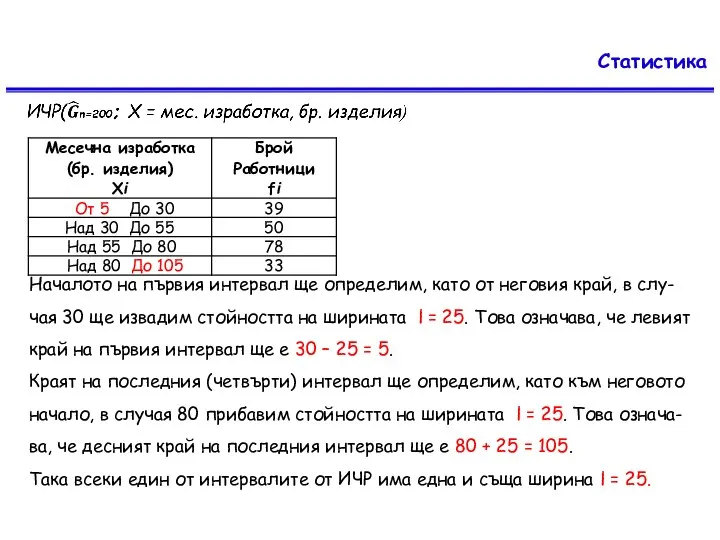
слу-чая 30 ще извадим стойността на ширината l = 25. Това означава, че левият край на първия интервал ще е 30 – 25 = 5.
Краят на последния (четвърти) интервал ще определим, като към неговото начало, в случая 80 прибавим стойността на ширината l = 25. Това означа-ва, че десният край на последния интервал ще е 80 + 25 = 105.
Така всеки един от интервалите от ИЧР има една и съща ширина l = 25.
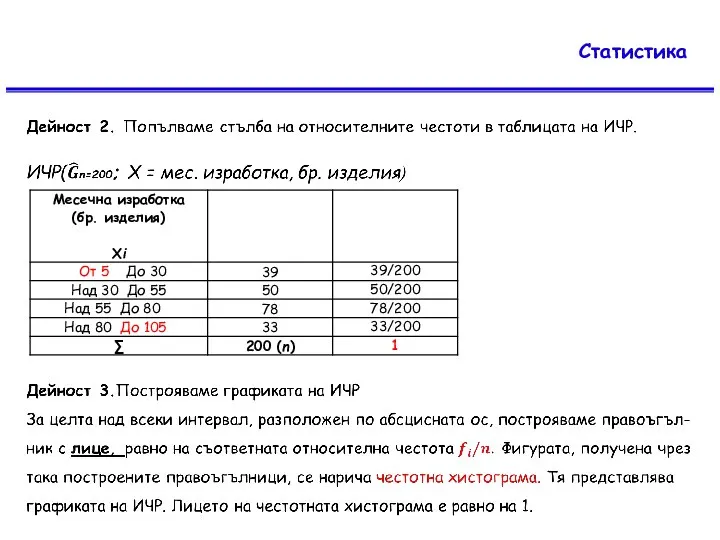
Слайд 7Статистика
Честотна хистограма
Начупената линия от отсечки, свързващи двата края на основата на

честотната хистограма със средите на горните основи на съседните правоъгълници, се нарича полигон на ЧР.
Слайд 12Статистика
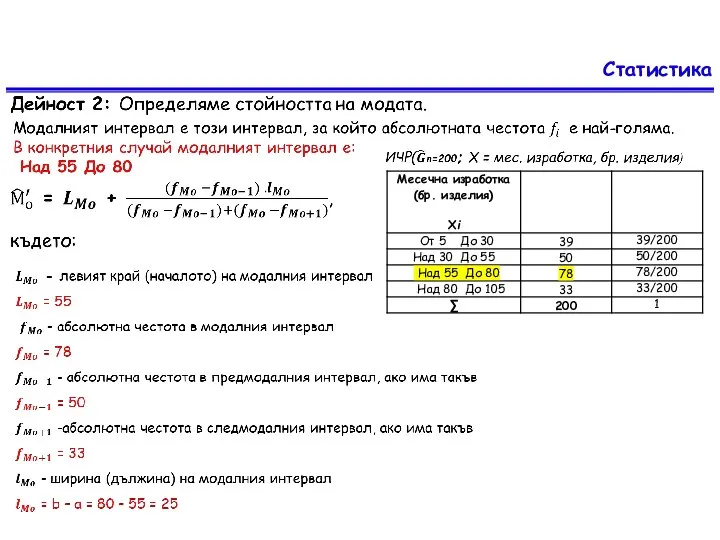
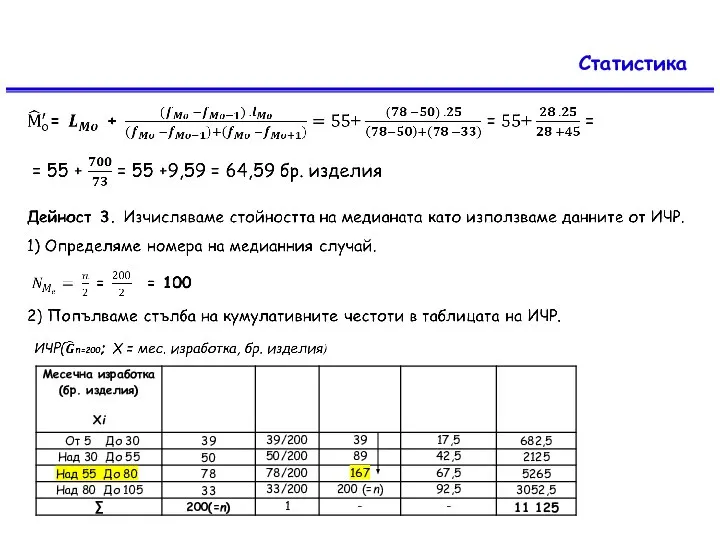
Медианният интервал е Над 55 До 80

Слайд 14Статистика
Изчисляваме стойността на медианата по правилото.
















 Новогодняя викторина Я люблю математику I тур Арифметический
Новогодняя викторина Я люблю математику I тур Арифметический График линейной функции с модулем
График линейной функции с модулем Числовые промежутки
Числовые промежутки Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам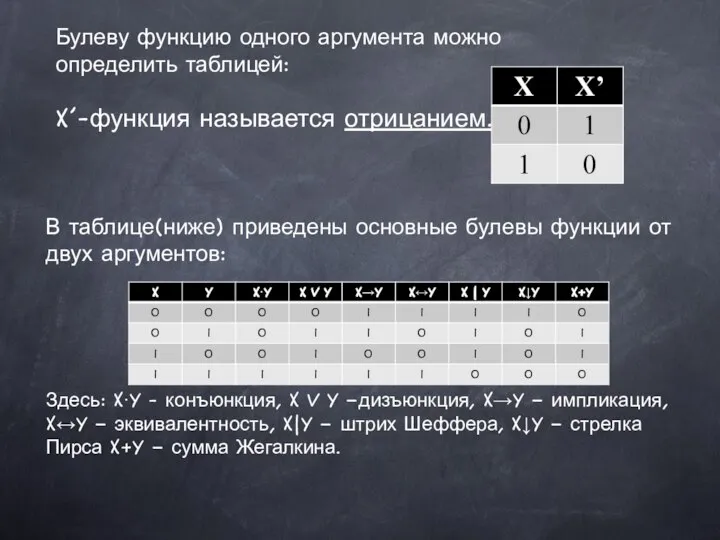 Булевы функции
Булевы функции Пропорциональность величин
Пропорциональность величин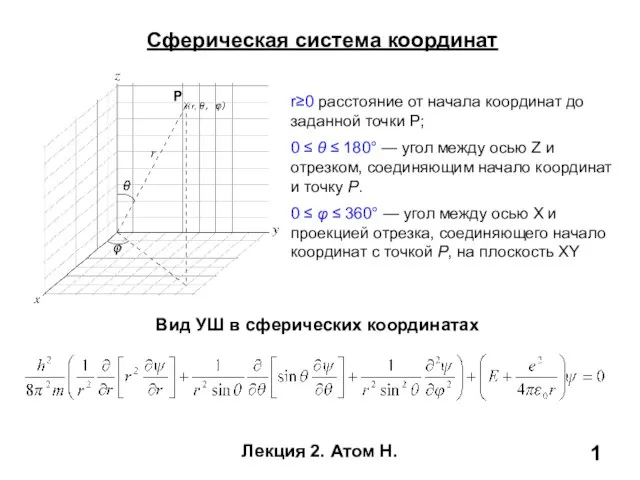 Сферическая система координат
Сферическая система координат История арабских чисел
История арабских чисел Квадратные уравнения
Квадратные уравнения Математика и я
Математика и я Дифференциальные исчисления функции одной независимой переменной
Дифференциальные исчисления функции одной независимой переменной Розв'язування типових задач
Розв'язування типових задач Знакомая незнакомка. Парабола
Знакомая незнакомка. Парабола Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень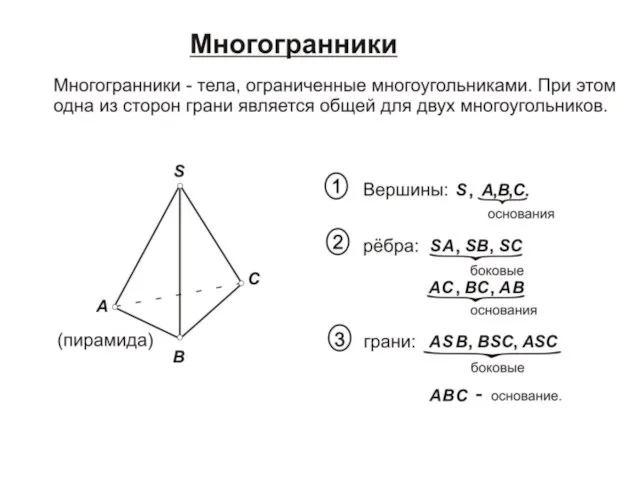 Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5 Метрология
Метрология Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Ikeldilen argumentiň trigonometrik funksiýalary
Ikeldilen argumentiň trigonometrik funksiýalary Физический и геометрический смысл производной. Понятие дифференциал функции
Физический и геометрический смысл производной. Понятие дифференциал функции Выражение F
Выражение F Показательные уравнения и неравенства
Показательные уравнения и неравенства Умножение обыкновенных дробей
Умножение обыкновенных дробей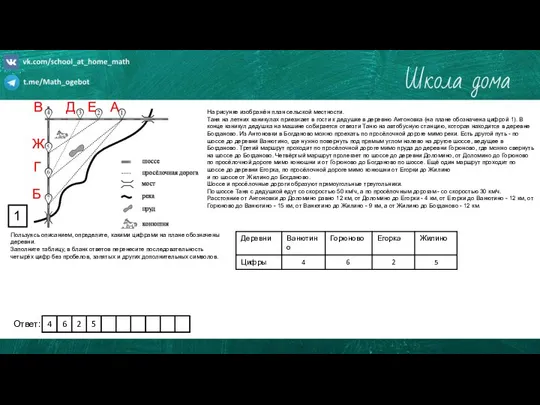 Практико-ориентированное задание
Практико-ориентированное задание Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Периметр многогранника
Периметр многогранника