Содержание
- 2. Обучающие: «открыть»понятия перпендикуляра и наклонной к плоскости; формировать умения: читать чертеж; применять определение прямой, перпендикулярной к
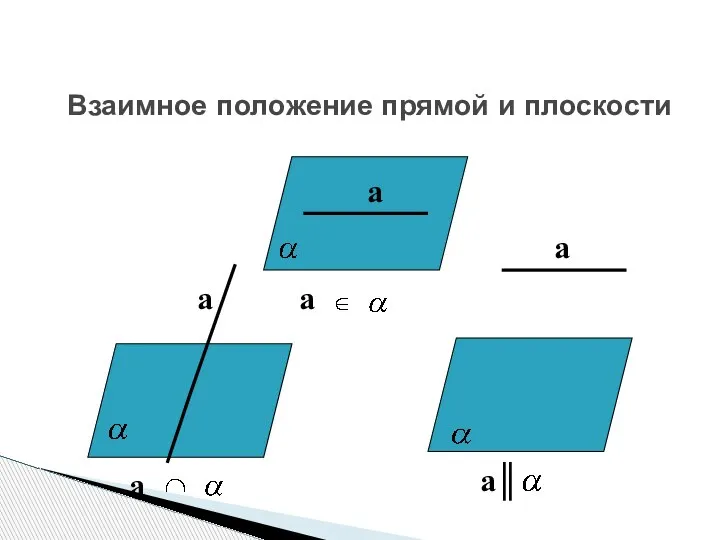
- 3. Взаимное положение прямой и плоскости a a║ a a a a
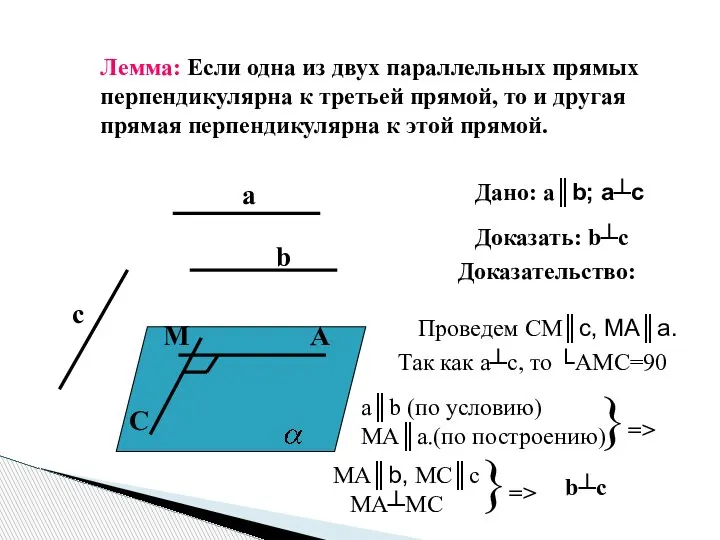
- 5. Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна
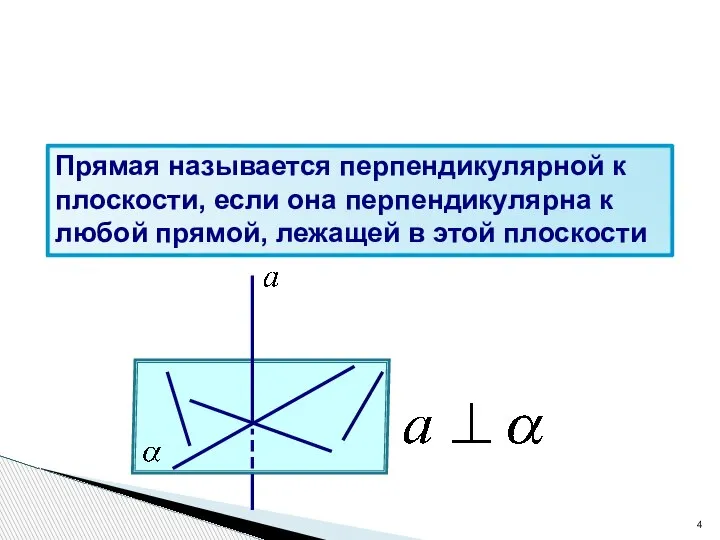
- 6. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой
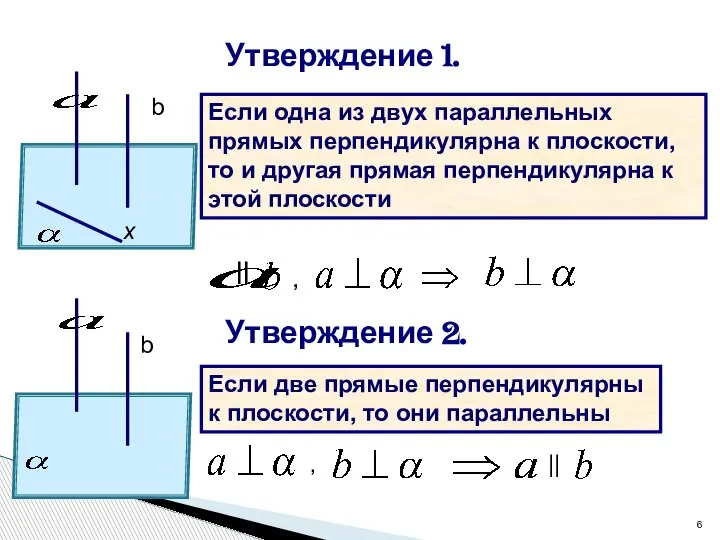
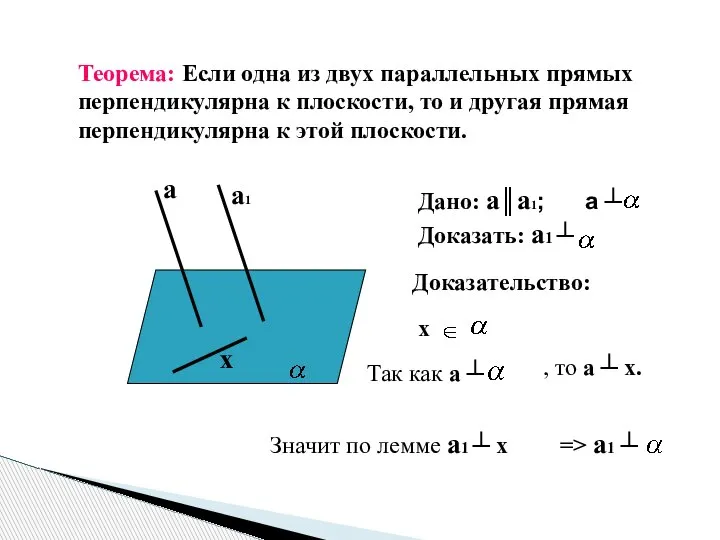
- 7. а а1 х Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая
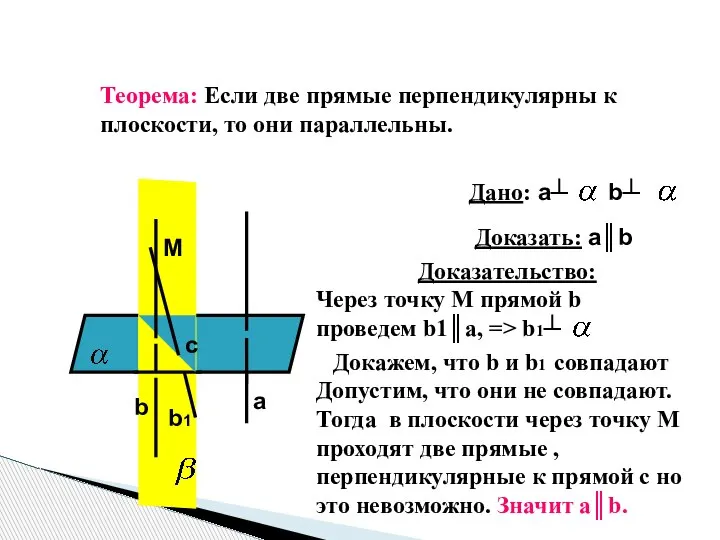
- 8. Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны. M c a b b1 Дано:
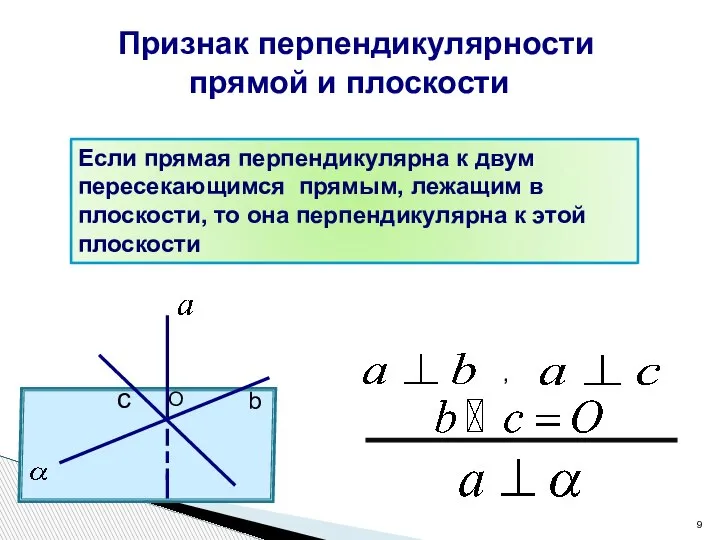
- 9. Признак перпендикулярности прямой и плоскости b c , O
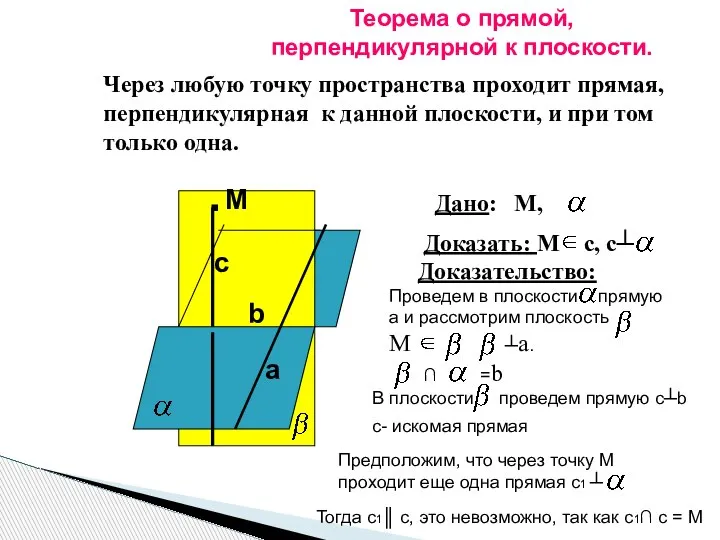
- 10. . M a b c Теорема о прямой, перпендикулярной к плоскости. Через любую точку пространства проходит
- 11. Устная работа №3 Сторона АВ правильного треугольника АВС лежит в плоскости . Может ли прямая BC
- 12. Прямая a перпендикулярна к плоскости , прямая b не перпендикулярна к плоскости . Могут ли прямые
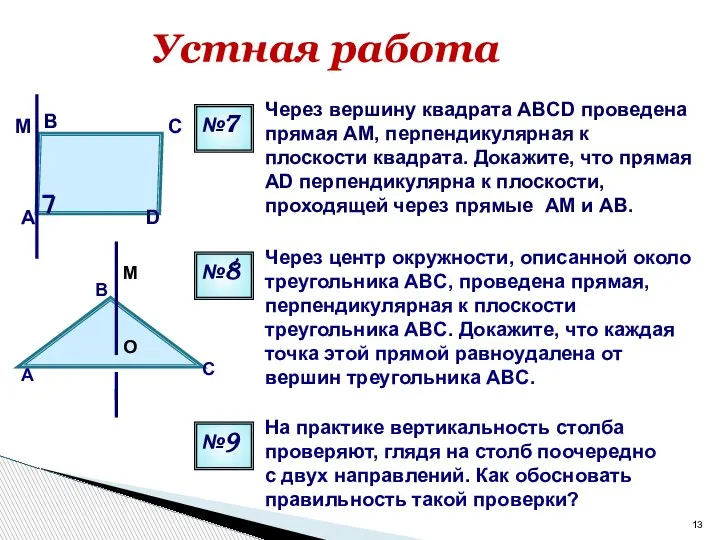
- 13. Через вершину квадрата ABCD проведена прямая AM, перпендикулярная к плоскости квадрата. Докажите, что прямая AD перпендикулярна
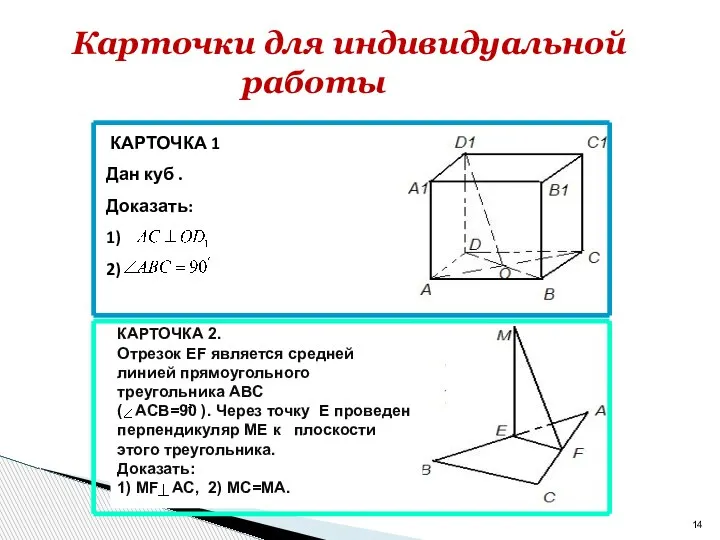
- 14. КАРТОЧКА 2. Отрезок EF является средней линией прямоугольного треугольника ABC ( ACB=90 ). Через точку E
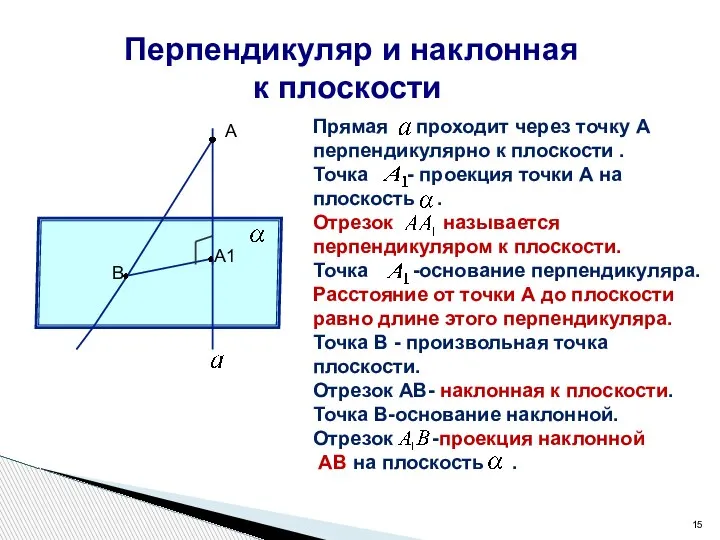
- 15. Перпендикуляр и наклонная к плоскости А А1 В Прямая проходит через точку А перпендикулярно к плоскости
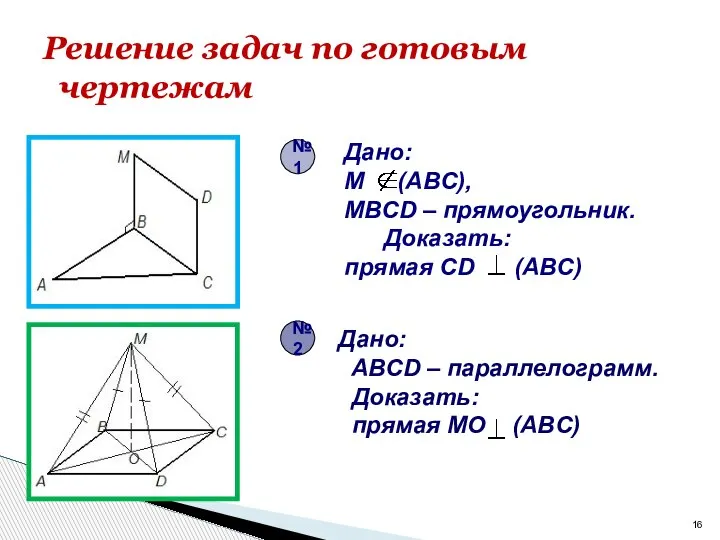
- 16. Решение задач по готовым чертежам Дано: M (ABC), MBCD – прямоугольник. Доказать: прямая CD (ABC) Дано:
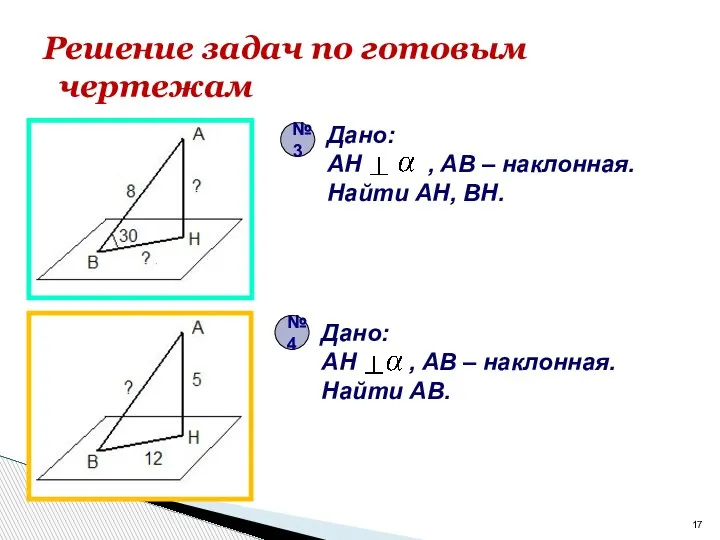
- 17. Решение задач по готовым чертежам Дано: AH , AB – наклонная. Найти AB. Дано: AH ,
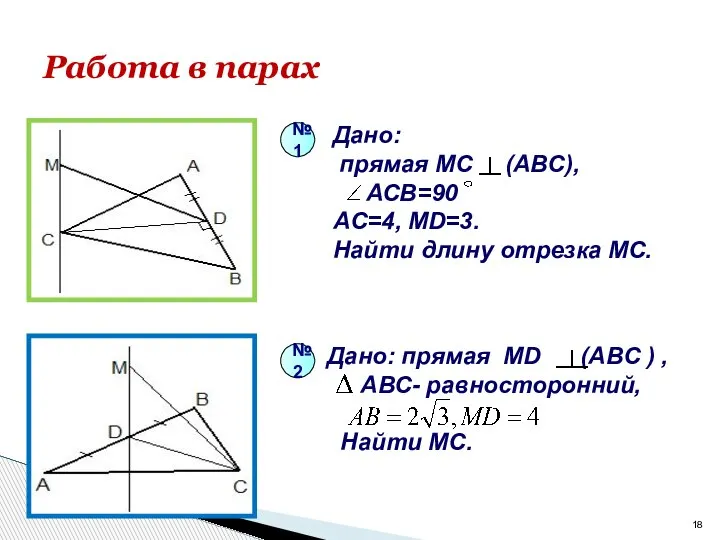
- 18. Работа в парах Дано: прямая МС (АВС), АСВ=90 AC=4, MD=3. Найти длину отрезка MC. Дано: прямая
- 20. Самостоятельная работа.
- 22. Скачать презентацию





 Разложение на множители с помощью формул
Разложение на множители с помощью формул Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Подобие треугольников
Подобие треугольников Логика - это русло мысли
Логика - это русло мысли Цели урока:
Цели урока: Теорема Виета
Теорема Виета Подготовка к контрольной работе
Подготовка к контрольной работе Системы принятия решений. Определения
Системы принятия решений. Определения Игра в стручки
Игра в стручки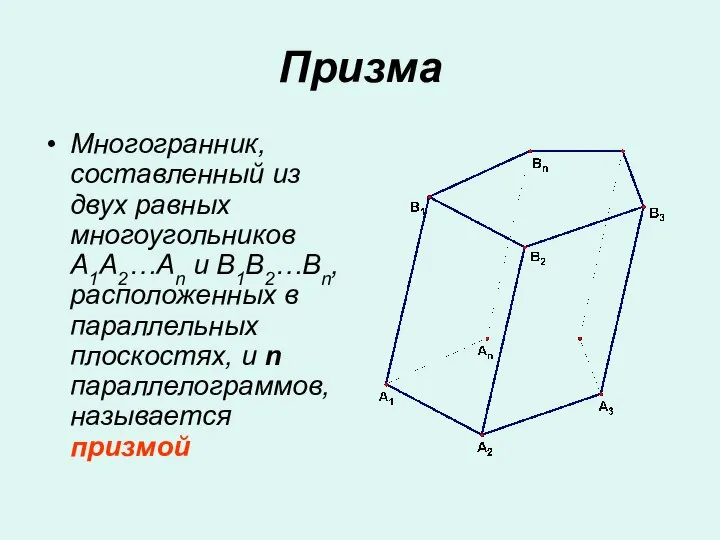 Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Нетрадиционные пособия по математическому развитию дошкольников (работа муниципального методического объединения воспитателей)
Нетрадиционные пособия по математическому развитию дошкольников (работа муниципального методического объединения воспитателей) Тригонометрические функции и их графики
Тригонометрические функции и их графики Квадратные уравнения. Задания
Квадратные уравнения. Задания Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Разные задачи (6 класс)
Разные задачи (6 класс) Вавилонская математика
Вавилонская математика Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг Производная по направлению. Градиент и его свойства
Производная по направлению. Градиент и его свойства Изучение основ Анализа формальных понятий
Изучение основ Анализа формальных понятий Позиционные задачи
Позиционные задачи Арифметико-логические устройства. Устройства управления
Арифметико-логические устройства. Устройства управления Скалярное произведение векторов
Скалярное произведение векторов Цифра 2
Цифра 2 Использование производной
Использование производной тригонометрические неравенства
тригонометрические неравенства Математична Legoманiя
Математична Legoманiя