Системы счисления

СОДЕРЖАНИЕ
Определение системы счисления
Классификация систем счисления
Непозиционные и позиционные
По числу символов
Правила перевода из одной системы в другую
Перевод из десятичной в двоичную
Перевод из двоичной в десятичную
Перевод и десятичной в шестнадцатеричную
Перевод и шестнадцатеричной в десятичную
Двоичная арифметика
Сложение
Вычитание
Умножение
Деление
Контрольные вопросы

ОПРЕДЕЛЕНИЕ СИСТЕМЫ СЧИСЛЕНИЯ

ОПРЕДЕЛЕНИЕ СИСТЕМЫ СЧИСЛЕНИЯ
Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления – это способ представления чисел и соответствующие ему правила действий над числами. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Функции системы счисления:
даёт представления множества чисел (целых и/или вещественных*);
даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
отражает алгебраическую и арифметическую структуру чисел.
*Вещественными числами называются все положительныечисла, отрицательные числа и ноль.

КЛАССИФИКАЦИЯ СИСТЕМ СЧИСЛЕНИЯ

ПОЗИЦИОННЫЕ И НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Позиционными называются системы счисления, в которых значение цифры зависит от ее места (позиции) в записи числа.
Позиционной является привычная для нас в повседневной жизни десятичная система счисления, в которой значение (вес) цифры зависит от ее позиции в записи числа. В числе 1111 одна и та же цифра 1 означает последовательно единицу, десяток, сотню, тысячу.
Все системы счисления, используемые в информатике (двоичная, восьмеричная, шестнадцатеричная и т. д.), являются позиционными. Это важно, т. к. правила образования чисел, перевода из одной системы в другую, выполнения арифметических операций во всех позиционных системах аналогичны.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Непозиционными называются системы счисления, в которых значение цифры не зависит от ее места (позиции) в записи числа.
Непозиционной системой счисления является, например, римская. Правила выполнения арифметических операций в непозиционных системах счисления совсем иные
Египетская система счисления – десятичная непозиционная система счисления

КЛАССИФИКАЦИЯ СИСТЕМ СЧИСЛЕНИЯ ПО ЧИСЛУ СИМВОЛОВ

САМЫЕ РАСПРОСТРАНЕННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Самые распространенные системы счисления:
Двоичную систему счисления
Троичную систему счисления
Восьмеричную систему счисления
Десятичную систему счисления
Шестнадцатеричную систему счисления

ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ

ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах.
В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 510, в двоичной 1012. Иногда двоичное число обозначают префиксом 0b или символом & (амперсанд), например 0b101 или соответственно &101.
В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».

ТРОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Трои́чная систе́ма счисле́ния — позиционная система счисления с целочисленным основанием, равным 3.
В распечатках ЭВМ «Сетунь» использовалось кодирование {1,0,1}. Троичные цифры можно обозначать любыми тремя знаками {A,B,C}, но при этом дополнительно нужно указать старшинство знаков, например, A
Практическое применение:
Работая в палате мер и весов, Д. И. Менделеев, с учётом симметричной троичной системы счисления, разработал цифровой ряд значений весов разновеса для взвешивания на лабораторных весах, который используется по сей день.
В распечатках ЭВМ «Сетунь» использовалось кодирование {1,0,1}. Троичные цифры можно обозначать любыми тремя знаками {A,B,C}, но при этом дополнительно нужно указать старшинство знаков, например, A
«Се́тунь» — малая ЭВМ на основе троичной логики, разработанная в вычислительном центре Московского государственного университета в 1959 году.
Трайт — минимальная непосредственно адресуемая единица главной памяти «Сетуни-70» Брусенцова. Трайт равен 6 тритам (почти 9,51 бита). В «Сетуни-70» интерпретируется как знаковое целое число в диапазоне от −364 до 364. Трайт достаточно велик, чтобы закодировать, например, алфавит, включающий русские и латинские буквы (включая заглавные и строчные), цифры, математические и служебные знаки. В трайте может содержаться целое число как девятеричных, так и двадцатисемеричных цифр.

ТРОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры {0,1,2}, а в троичной симметричной системе счисления знаки {−,0,+}, {−1,0,+1}, {1,0,1}, {1,0,1}, {i,0,1}, {N,O,P}, {N,Z,P} и цифры {2,0,1}, {7,0,1}.

ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты* двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
*Триплет — комбинация из трёх последовательно расположенных чисел.

ПРИМЕНЕНИЕ ВОСЬМЕРИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах.
Восьмеричная система счисления употребляется в ЭВМ как вспомогательная для записи информации в сокращённом виде. Ранее широко использовалась в программировании и компьютерной документации, в настоящее время почти полностью вытеснена 16-ричной.

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев на руках у человека.
Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Десятичная непозиционная система счисления с единичным кодированием десятичных цифр (от 1 до 1 000 000) возникла во второй половине третьего тысячелетия до н. э. в Древнем Египте (египетская система счисления*).
*Египетская система счисления — непозиционная система счисления, которая употреблялась в Древнем Египте вплоть до начала X века н. э. В этой системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100 и т. д. до миллиона.

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Древнейшая известная запись позиционной десятичной системы обнаружена в Индии в 595 г. Нуль в то время применялся не только в Индии, но и в Китае. В этих старинных системах для записи одинакового числа использовались символы, рядом с которыми дополнительно помечали, в каком разряде они стоят. Потом перестали помечать разряды, но число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, её нужно пометить нулём. В поздних вавилонских текстах такой знак стал появляться, но в конце числа его не ставили. Лишь в Индии нуль окончательно занял своё место, эта запись распространилась затем по всему миру.
Индийская нумерация пришла сначала в арабские страны, затем и в Западную Европу. О ней рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на арабском, то за индийской нумерацией в Европе закрепилось иное название — «арабская» (арабские цифры).

ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонентов цвета (RGB) в шестнадцатеричном виде.

ПРИМЕНЕНИЕ ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.

ПРИМЕНЕНИЕ ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Использование MAC-адресов является одним из наиболее важных аспектов технологии локальной сети Ethernet. MAC-адреса используют шестнадцатеричную систему счисления.
В системе счисления с основанием 16 используются цифры от 0 до 9 и буквы от A до F. На рис. 1 показаны соответствующие десятичные и шестнадцатеричные значения для двоичного кода 0000—1111. Нам проще представить значение в виде одной шестнадцатеричной цифры, чем в виде четырёх двоичных битов.
Если 8 бит (байт) — это общепринятая бинарная группа, двоичный код 00000000—11111111 может быть представлен в шестнадцатеричной системе исчисления в качестве диапазона 00–FF. Чтобы заполнить 8-битное представление, всегда отображаются ведущие нули. Например, двоичное значение 0000 1010 показано в шестнадцатеричной системе как 0A.
Шестнадцатеричное значение обычно представлено в тексте значением, которое располагается после 0x (например, 0x73) или подстрочного индекса 16. В остальных, более редких случаях, за ним может располагаться H (например, 73H). Однако, поскольку подстрочный текст не распознаётся в командной строке или средах программирования, перед техническим представлением шестнадцатеричных значений стоит «0x» (нулевой Х). Так, приведённые выше примеры будут отображаться как 0x0A и 0x73 соответственно.
Шестнадцатеричная система счисления используется для представления MAC-адресов Ethernet и IP-адресов версии 6.

ПРАВИЛА ПЕРЕВОДА ИЗ ОДНОЙ СИСТЕМЫ В ДРУГУЮ

ПРАВИЛА ПЕРЕВОДА ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДВОИЧНУЮ

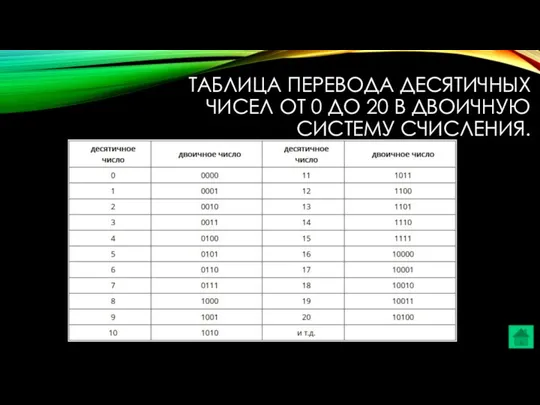
ТАБЛИЦА ПЕРЕВОДА ДЕСЯТИЧНЫХ ЧИСЕЛ ОТ 0 ДО 20 В ДВОИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ.

МЕТОД ПЕРВЫЙ: СОКРАЩЕННОЕ ДЕЛЕНИЕ С ОСТАТКОМ
Чтобы перевести целое положительное десятичное число в двоичную систему счисления, нужно это число разделить на 2. Полученное частное снова разделить на 2, и дальше до тех пор, пока частное не окажется меньше 2. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
46 = 1011102

МЕТОД ВТОРОЙ: СРАВНЕНИЕ УМЕНЬШАЮЩИХСЯ СТЕПЕНЕЙ И ВЫЧИТАНИЕ
Допустим, требуется перевести число 637 десятичной системы в двоичную систему. Делается это следующим образом:
Отыскивается максимальная степень двойки, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т.к. 29 = 512, а 210 = 1024, что больше нашего начального числа. Таким образом, мы получили число разрядов результата. Оно равно 9+1=10. Значит, результат будет иметь вид 1ххххххххх, где вместо х может стоять 1 или 0.
Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 637-29=125. Затем сравниваем с числом 28=256. Так как 125 меньше 256, то девятый разряд будет 0, т.е. результат уже примет вид 10хххххххх.

27=128 > 125, значит и восьмой разряд будет нулём.
26=64, то седьмой разряд равен 1.
125-64=61 Таким образом, мы получили четыре старших разряда и число примет вид 10011ххххх.
25=32 и видим, что 32 < 61, значит шестой разряд равен 1 (результат 100111хххх), остаток 61-32=29.
24=16 < 29 - пятый разряд 1 => 1001111ххх. Остаток 29-16=13.
23=8 < 13 => 10011111хх. 13-8=5.
22=4 < 5 => 10011111хх, остаток 5-4=1.
21=2 > 1 => 100111110х, остаток 2-1=1. 20=1 => 1001111101. Это и будет конечный результат.

ПЕРЕВОД ДРОБНОГО ДЕСЯТИЧНОГО ЧИСЛА В ДВОИЧНОЕ
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример 1: Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 - целая часть, которая станет первой цифрой результата),
0.25·2 = 0.5 (0 - вторая цифра результата),
0.5·2 = 1.0 (1 - третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.12510 = 0.0012

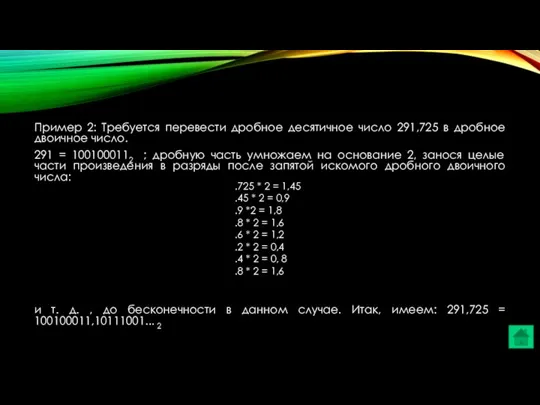
Пример 2: Требуется перевести дробное десятичное число 291,725 в дробное двоичное число.
291 = 1001000112 ; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
и т. д. , до бесконечности в данном случае. Итак, имеем: 291,725 = 100100011,10111001... 2
.725 * 2 = 1,45
.45 * 2 = 0,9
.9 *2 = 1,8
.8 * 2 = 1,6
.6 * 2 = 1,2
.2 * 2 = 0,4
.4 * 2 = 0, 8
.8 * 2 = 1,6

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ПРАВИЛА ПЕРЕВОДА ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ

МЕТОД ПЕРВЫЙ: ИСПОЛЬЗУЯ ПОЗИЦИОННУЮ НОТАЦИЮ
Для преобразования числа из двоичной системы в десятичную необходимо пронумеровать разряды двоичного числа справа налево, начиная с 0, после чего сложить степени числа 2, умноженные на значение соответствующего разряда.

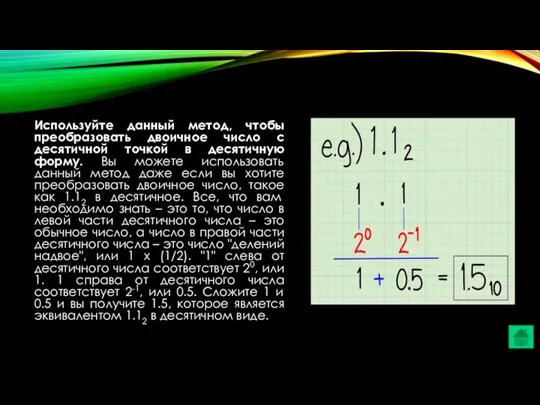
100110112 = 155

Используйте данный метод, чтобы преобразовать двоичное число с десятичной точкой в десятичную форму. Вы можете использовать данный метод даже если вы хотите преобразовать двоичное число, такое как 1.12 в десятичное. Все, что вам необходимо знать – это то, что число в левой части десятичного числа – это обычное число, а число в правой части десятичного числа – это число "делений надвое", или 1 x (1/2). "1" слева от десятичного числа соответствует 20, или 1. 1 справа от десятичного числа соответствует 2-1, или 0.5. Сложите 1 и 0.5 и вы получите 1.5, которое является эквивалентом 1.12 в десятичном виде.

МЕТОД ВТОРОЙ: ИСПОЛЬЗУЯ УДВОЕНИЕ
Данный метод не использует степени. Поэтому он проще для преобразования больших чисел в голове – вам нужно только все время помнить итог. Предположим, вы работаете с числом 10110012.
Начиная слева, удвойте ваш предыдущий итог и добавьте текущую цифру. Так как вы работаете с двоичным числом 10110012, ваша первая цифра слева равна 1. Ваш предыдущий итог равен 0, так как вы еще не начали. Вам необходимо удвоить предыдущий итог, 0, и добавить 1, текущую цифру. 0 x 2 + 1 = 1, так что ваш новый итог равен 1.

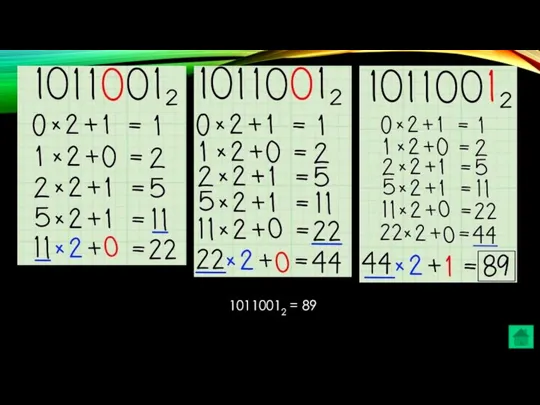
Удвойте ваш текущий итог и добавьте следующую цифру слева. Ваш текущий итог равен 1, а ваша новая цифра 0. Так что удвойте 1 и добавьте 0. 1 x 2 + 0 = 2. Ваш новый итог равен 2.
Выполняя каждый раз одно и тоже действие, у вас должно получиться следующее:

10110012 = 89

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ПРАВИЛА ПЕРЕВОДА ИЗ
ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
В шестнадцатеричной системе счисления существует таблица соответствия десятичных и шестнадцатеричных чисел, которая используется при переводе из одной системы в другую:

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
В свое же время для перевода из десятичной системы счисления, число нужно делить на 16 до тех пор пока оно не сможет разделиться. Из остатков при делении составляется число в шестнадцатеричной системе счисления справа налево.
Например переведем число 1356 из десятичной системы счисления в шестнадцатеричную:
Ответ: 135610 = 54C16

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
Также для примера возьмем число побольше, например 9656, и переведем его шестнадцатеричную систему счисления:
Можно заметить, что в остатке у нас есть число 11, которое по правилам таблицы соответствия десятичных и шестнадцатеричных чисел, заменяется на символ «В» при переводе числа.
Ответ: 965610 = 25B816

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ПРАВИЛА ПЕРЕВОДА ИЗ ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ

ПЕРЕВОД ИЗ ШЕСТНАДЦАТЕРИЧНОЙ
СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
Для перевода числа из любой системы счисления в десятичную существует общая формула:
Для перевода из шестнадцатеричной системы счисления в десятичную преобразуем формулу:
Возьмем для примера:
Ответ: A2F16 = 260710

ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
Также можно переводить дробные числа из шестнадцатеричной системы счисления в десятичную.
Например:
Ответ: 0,2A916 = 0,16625976562510
Ответ: 104,F216 = 260,945312510

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ДВОИЧНАЯ АРИФМЕТИКА

ДВОИЧНАЯ АРИФМЕТИКА
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.

СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

ВЫЧИТАНИЕ ДВОИЧНЫХ ЧИСЕЛ

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

УМНОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения. Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

УМНОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

КОНТРОЛЬНЫЕ ВОПРОСЫ
Система счисления и её функции
Правила двоичного вычитания
Отличия позиционной и непозиционной системы счисления
Правила двоичного сложения
Основание системы счисления – это …?
Область применения восьмеричной системы счисления
Правила двоичного деления
История десятичной системы счисления
Правила двоичного умножения
Область применения шестнадцатеричной системы счисления