Теория вероятностей и математическая статистика. Лекция 6 ТВ

Лекция № 6
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
ДИСКРЕТНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН,
СВЯЗАННЫЕ С ПОВТОРНЫМИ
ИСПЫТАНИЯМИ

Биномиальное распределение (схема Бернулли)
Пример 1. Монета подбрасывается 4 раза, пусть X - означает число появившихся гербов.
Пример 2. Известно, что в определенном городе 30% горожан предпочитают добираться на работу личным автомобилем. Случайно выбраны 8 человек. Пусть Y - число людей в выборке, предпочитающих личный транспорт.
Пример 3. Известно, что 15% деталей, произведенных автоматом, - бракованные. В порядке случайного отбора взято 12 деталей. Пусть Z - число дефектных деталей.
Что характерно для случайных величин X, Y и Z?
Это – примеры ДСВ, подчиняющихся вероятностному закону распределения, известному как биномиальное распределение.
Биномиальное распределение базируется на эксперименте, состоящем в последовательности испытаний Бернулли (схеме повторных испытаний).

Испытания Бернулли - это последовательность n идентичных испытаний, удовлетворяющих следующим условиям:
1. Каждое испытание имеет два исхода, называемые успех и неуспех. Эти два исхода - взаимно несовместные и противоположные события.
2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q, где q=1 - p .
3. Все n испытаний - независимы. То есть вероятность наступления события в любом из испытаний не зависит от результатов других испытаний.
Случайная величина, для которой вычисляется число успехов в n повторных испытаниях, где p - вероятность успеха в любом из заданных испытаний, а q = (1 - p) -соответствующая вероятность неуспеха, подчиняется закону биномиального распределения с параметрами n и p.

Пример 1. Монета подбрасывается 4 раза, пусть ДСВ X - означает число появившихся гербов. При четырех подбрасываниях монеты случайная величина Х - число выпадений герба, принимает возможные значения Хi: 1,2,3,4.
Рассмотрим определенное событие, когда Х = 2.Событие состоит в том, что при 4-х подбрасываниях монеты 2 раза выпадет герб.
Определим вероятность этого события, то есть Р(Х=2). Подсчитаем, сколькими способами может осуществиться данное событие.
При 4-х бросаниях монеты герб появится два раза в одной из следующих 6-ти последовательностей:
ГГЦЦ, ГЦГЦ, ГЦЦГ, ЦГГЦ, ЦГЦГ, ЦЦГГ.
Исходя из независимости 4-х испытаний, вероятность любой последовательности, скажем (Г, Г, Ц, Ц) есть ppqq. Очевидно, что порядок появления цифры или герба не влияет на вероятность. Вероятность p2q2 есть вероятность для любой из 6-ти перечисленных комбинаций.
Поскольку все шесть возможных комбинаций ведут к событию Х=2, то умножим результат на 6, что даст нам 6p2q2. Для идеальной монеты p = q = 0,5; отсюда Р(Х=2) = 6(0,5)4= 0,375.
Точно также можно вычислить другие вероятности Р(Х=0), Р(Х=1), Р(Х=3),Р(Х=4).

Обобщим процедуру вычисления вероятности появления некоторого события точно m раз в n последовательных испытаниях, удовлетворяющих условиям схемы повторных испытаний:
1. Вероятность любой заданной последовательности, в которой событие появляется m раз в n испытаниях с вероятностью успеха в каждом отдельном испытании p и q - неуспеха, равна pmqn-m.
Для опыта с подбрасыванием монеты при p=q=0,5, n= 4 и m= 2 получим
Р(Х=2) = (0,5)2(0,5)2 = (0,5)4 .
2. Число различных комбинаций в испытаниях, в результате которых наступит точно m успехов, равно числу сочетаний из n элементов по m элементов в каждом:

3. Поскольку существует комбинаций и каждая комбинация имеет вероятность pmqn-m, то вероятность m успехов в n испытаниях есть результат двух описанных выше действий.
Будем использовать символ Pn,m для обозначения вероятности Р(Х=m) в n испытаниях с вероятностью успеха в каждом отдельном испытании – p:
где p - вероятность успеха в отдельном испытании, q=1-p, n - число испытаний, m - число успешных испытаний.
Это - формула Бернулли.
В формуле (1) m может принимать значения от 0 до n. Подставим m=0,1,2,...,n в (1).
Построим биномиальное распределение числа выпадений герба при 4-х подбрасываниях монеты.

Рассмотрим в качестве СВ Х число m наступления некоторого события в n независимых испытаниях. Очевидно, общее число появлений этого события в испытаниях состоит из суммы чисел появлений события в отдельных испытаниях, то есть Х=m=Х1+Х2+...+ +Хn, где Xi - число появлений события в i-том испытании (i=1,2,...,n). Так как вероятность наступления события в каждом испытании постоянна и равна р (не наступления - q), то для каждой случайной величины Хi имеем распределение вероятностей:

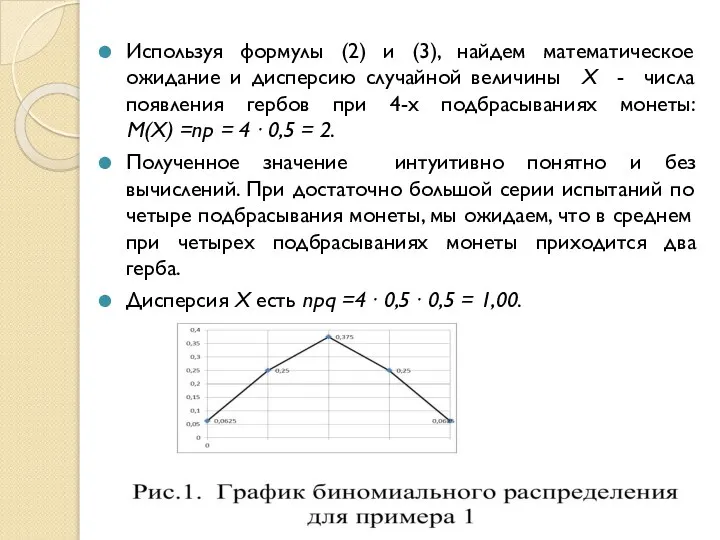
Используя формулы (2) и (3), найдем математическое ожидание и дисперсию случайной величины Х - числа появления гербов при 4-х подбрасываниях монеты: М(Х) =np = 4 ∙ 0,5 = 2.
Полученное значение интуитивно понятно и без вычислений. При достаточно большой серии испытаний по четыре подбрасывания монеты, мы ожидаем, что в среднем при четырех подбрасываниях монеты приходится два герба.
Дисперсия Х есть npq =4 ∙ 0,5 ∙ 0,5 = 1,00.

Как видно из графика на рисунке 1 при m=2 вероятность достигает максимального значения.
Частота m, равная 2, называется вероятнейшим числом или вероятнейшей частотой (наивероятнейшей).
Вероятнейшей частотой наступления события называется та частота, при которой вероятность достигает своего наибольшего значения и обозначается m0:
np - q≤m0≤np + p (5)
В этом неравенстве m0 может быть только целым числом.
Замечание: Если np - целое число, то m0 = np.
Пример 2. Вероятность того, что выписанный продавцом чек будет оплачен, равна 0,9. Какое наивероятнейшее число чеков будет оплачено, если выписано 40 чеков?
Находим произведение np=40∙0,9=36 (целое число), значит, m0=36.
Найдем m0 по формуле (5): 40∙0,9 - 0,1 ≤m0≤40∙0,9 + 0,9
35,9 ≤m0≤36,9
Какое целое число удовлетворяет этому двойному неравенству? m0=36.

Распределение Пуассона

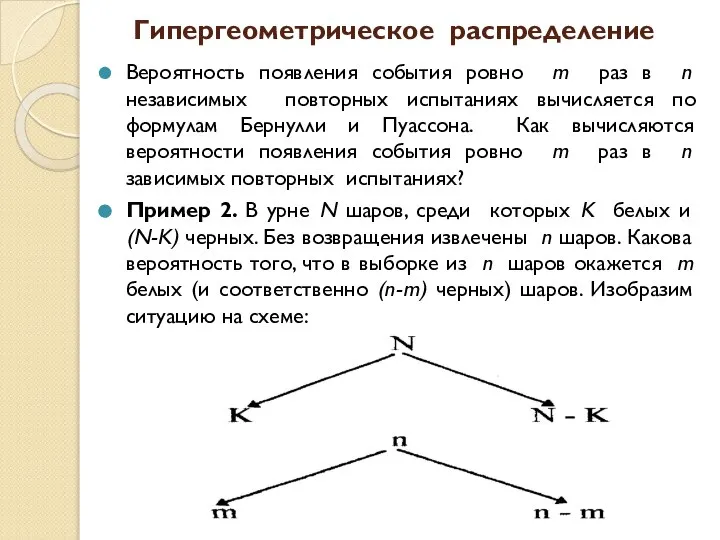
Гипергеометрическое распределение
Вероятность появления события ровно m раз в n независимых повторных испытаниях вычисляется по формулам Бернулли и Пуассона. Как вычисляются вероятности появления события ровно m раз в n зависимых повторных испытаниях?
Пример 2. В урне N шаров, среди которых K белых и (N-K) черных. Без возвращения извлечены n шаров. Какова вероятность того, что в выборке из n шаров окажется m белых (и соответственно (n-m) черных) шаров. Изобразим ситуацию на схеме: