Исследование функций

Знаете ли вы,
что называется ...
областью определения функции;
корнями (нулями) функциикорнями (нулями) функции;
промежутками постоянного знакапромежутками постоянного знака;
наибольшим (наименьшим) значением функции?
множеством значений функции;
промежутками монотонностипромежутками монотонности;
точками экстремуматочками экстремума;
?
Выход

Нет?!
Попробуем разобраться?
Да?!
Хочешь проверить свои знания?
Выход

Нет?!
Попробуем разобраться?
Да?!
Хочешь проверить свои знания?
легкий
Выбери уровень сложности:
трудный
средний
Выход

Область определения функции
y = f (x)
Область определения функции
[а; b]
иначе: а < x < b
Область определения функции - это те значения аргумента, при которых функция задана, определена
Геометрически - это проекция графика функции на ось Ох
a
b
0
x
y
y = f (x)

Множество значений функции
y = f (x)
Множество
значений
функции
[m; M]
иначе: m < y < M
Множество значений функции - это множество чисел, состоящее из всех значений функции
Геометрически - это проекция графика функции на ось Оy
0
x
y
m
M
y = f (x)

Корни (нули) функции
y = f (x)
Корни
функции
f (x) = 0
х = х1;
х = х2;
х = х3.
Корни функции - это точки, в которых функция обращается в нуль. Эти точки являются решениями уравнения f(x) = 0
Геометрически - это абсциссы точек пересечения графика функции с осью Ох
x
y
х1
х2
х3
0
y = f (x)

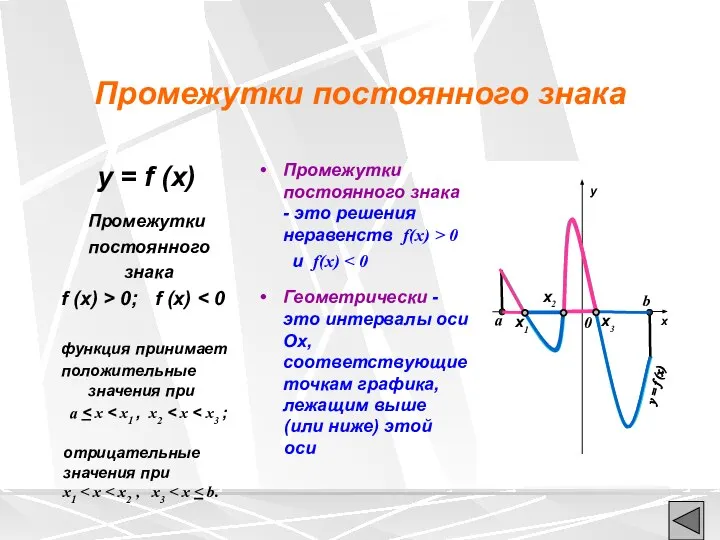
Промежутки постоянного знака
y = f (x)
Промежутки
постоянного
знака
f (x) > 0; f (x) < 0
функция принимает
положительные значения при
a < x < x1 , x2 < x < x3 ;
Промежутки постоянного знака - это решения неравенств f(x) > 0
Геометрически - это интервалы оси Ох, соответствующие точкам графика, лежащим выше
x
y
х1
х2
х3
0
a
b
и f(x) < 0
(или ниже) этой оси
отрицательные значения при
х1 < x < x2 , x3 < x < b.
y = f (x)

Промежутки монотонности
y = f (x)
Промежутки монотонности
функции
функция возрастает при m1 < x < m2
и при m3 < x < b;
Промежутки монотонности - это промежутки оси Ох, на которых функция возрастает (промежутки возрастания)
Геометрически - это интервалы оси Ох, где график функции идет вверх
a
b
0
x
y
m1
m2
m3
или убывает (промежутки убывания)
функция убывает при a < x < m1
и при m2 < x < m3 .
или вниз
y = f (x)

Точки экстремума функции
y = f (x)
Точки экстремума
х = m2 - точка максимума;
x = m1, x = m3 - точки минимума
Точки экстремума - точки, лежащие внутри области определения, в которых функция принимает самое большое (максимум) или самое малое (минимум) значение по сравнению со значениями в близких точках
Геометрически - около точек экстремума график выгибается вверх или вниз
0
x
y
m1
m2
m3
min
min
max
внутри
y = f (x)

Наибольшее и наименьшее значение функции
y = f (x)
Наибольшее значение функции
f(x) = М при х = m2,
Говорят, что в точке х0 функция f принимает наибольшее (наименьшее) значение, если f(x0) > f(x)
(f(x0) < f(x)) для любого значения х. Само число f(x0) называется наибольшим (наименьшим) значением функции
Геометрически - это ординаты самой высокой (самой низкой) точки графика
0
x
y
m
m2
m3
М
наименьшее значение функции
f(x) = m при х = m3.
М
m2
m3
m
y = f (x)

Проверь себя
Проведите полное исследование функции, заданной графически.
1. Область определения функции y = f(x)
2. Множество значений функции у = f(x)
3. Корни функции у = f(x)
4. Промежутки постоянного знака функции у = f(x)
f(x) > 0 при х < -2; -1,4 < x < 1,4; x > 2;
f(x) < 0 при -2 < x < -1,4; 1,4 < x < 2.
5. Функция у = f(x) возрастает
при -1,7 < х < 0 и при x > 1,7.
Функция у = f(x) убывает
при х < -1,7 и при 0 < x < 1,7.
6. Точки экстремума:
0
x
y
2
2
-1
y = f (x)
-1,7
-1,4
1,4
1,7
7. Наибольшее значение функции y = f(x)
Наименьшее значение функции y = f(x)
х - любое число.
y > - 1.
f(x) = 0: x = -2; x = -1,4; x = 1,4; x = 2.
x = 0 - точка максимума;
x = -1,7, x = 1,7 - точки минимума.
не существует.
у = -1 при х = -1,7, х = 1,7.
- 2
Уровень сложности: легкий

Проверь себя
Проведите полное исследование функции, заданной графически.
1. Область определения функции y = f(x)
2. Множество значений функции у = f(x)
3. Корни функции у = f(x)
4. Промежутки постоянного знака функции у = f(x)
f(x) > 0 при 0 < x < 1;
f(x) < 0 при x < 0, x >1.
5. Функция у = f(x) возрастает
нет.
Функция у = f(x) убывает
6. Точки экстремума:
0
x
y
y = f (x)
7. Наибольшее значение функции y = f(x)
Наименьшее значение функции y = f(x)
x < 0, x > 0.
y < - 1, y > - 1.
f(x) = 0: x = 1.
нет
не существует.
не существует.
Уровень сложности: средний
1
-1
при x < 0 и при x > 0.

Проверь себя
Проведите полное исследование функции, заданной графически.
1. Область определения функции y = f(x)
2. Множество значений функции у = f(x)
3. Корни функции у = f(x)
4. Промежутки постоянного знака функции у = f(x)
f(x) > 0 при х < -2; -1 < x < 1; x > 2;
f(x) < 0 при -2 < x < -1; 1 < x < 2.
5. Функция у = f(x) возрастает
при х < -2 и при -2 < х < 0.
Функция у = f(x) убывает
при 0 < x < 2 и при x > 2.
6. Точки экстремума:
0
x
y
y = f (x)
7. Наибольшее значение функции y = f(x)
Наименьшее значение функции y = f(x)
х < -2; -2 < x < 2; x > 2 .
y – любое число.
f(x) = 0: x = - 1; x = 1.
x = 0 - точка максимума.
не существует.
Уровень сложности: трудный
-2
-1
1
2
1
не существует.

При создании презентации использовалась литература:
Башмаков М.И. Уроки математики. Вып.2. - Глядя на график. Учеб. Для учащихся ст. кл. с гуманитарным профилем обучения. - СПб.: Издательство «СВЕТ». 1995.