Содержание
- 2. METODE NUMERICE – curs 10 ? rezolvarea problemei → găsirea unei funcţii cu o expresie în
- 3. METODE NUMERICE – curs 10 Exemplu: aproximare cu polinoame algebrice aproximare cu polinoame trigonometrice
- 4. METODE NUMERICE – curs 10 ⮚ Distanţele uzual folosite pentru cazul discret (f este cunoscută printr-un
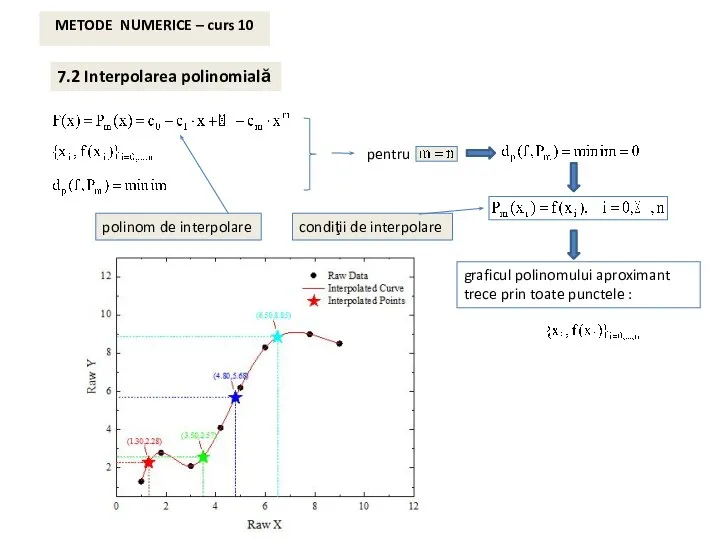
- 5. METODE NUMERICE – curs 10 7.2 Interpolarea polinomială pentru graficul polinomului aproximant trece prin toate punctele
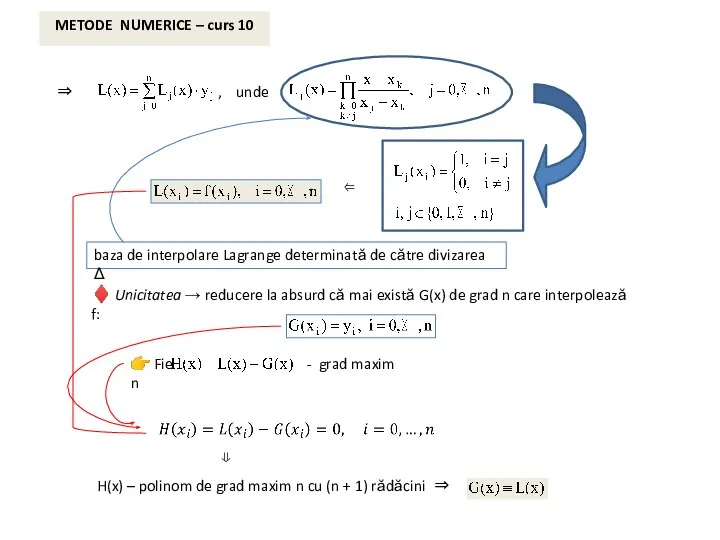
- 6. METODE NUMERICE – curs 10 7.2.1 Interpolarea Lagrange Demonstraţie: ♦ Existenţa → polinomul Lagrange Lj(x)
- 7. METODE NUMERICE – curs 10 ⇒ , unde ⇐ baza de interpolare Lagrange determinată de către
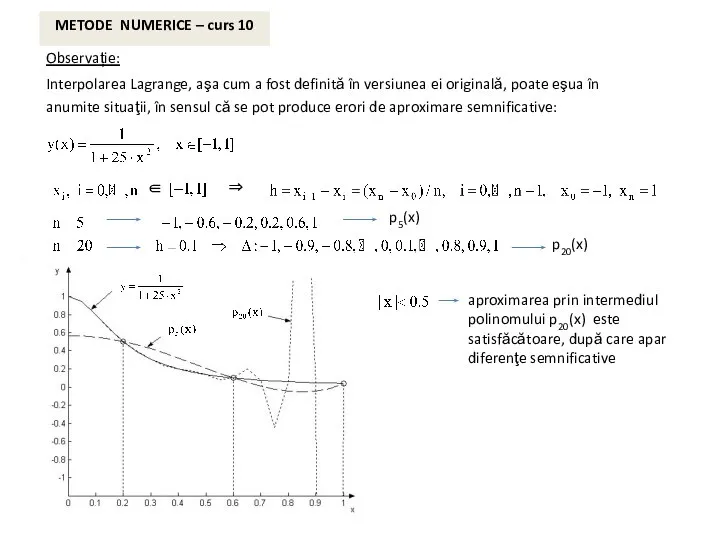
- 8. METODE NUMERICE – curs 10 Observație: Interpolarea Lagrange, aşa cum a fost definită în versiunea ei
- 9. METODE NUMERICE – curs 10 ideea de a nu folosi un polinom unic, care să aproximeze
- 10. METODE NUMERICE – curs 10 7.2.2 Interpolarea prin intermediul funcţiilor spline Funcţiile spline → funcţii formate
- 11. METODE NUMERICE – curs 10 Observaţie: m = 1 → funcţiile spline liniare m = 2
- 12. METODE NUMERICE – curs 10 Demonstraţia ? algoritmul de determinare a funcţiei - existenţa şi unicitatea
- 13. METODE NUMERICE – curs 10 (C3) condiţii de continuitate a funcţiei s’Δ(x): relaţii (C4) condiţii de
- 14. METODE NUMERICE – curs 10 Observaţii: funcţiile spline cubice naturale au proprietatea că au cea mai
- 15. METODE NUMERICE – curs 10 ⮚ aproximare în medie pătratică → se minimizează, în raport cu
- 17. Скачать презентацию











 Движение. Урок геометрии в 9 классе
Движение. Урок геометрии в 9 классе Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Занимательная математика.Игры с кубиками, 1 класс
Занимательная математика.Игры с кубиками, 1 класс Математика в логических упражнениях
Математика в логических упражнениях Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Объект и пространство
Объект и пространство Презентация на тему Мордкович А.Г. Профессор, автор, человек
Презентация на тему Мордкович А.Г. Профессор, автор, человек  Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Симметрия относительно точки
Симметрия относительно точки Презентация на тему Объем цилиндра
Презентация на тему Объем цилиндра  05_arif_dej_drob_2
05_arif_dej_drob_2 СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Математическая статистика
Математическая статистика Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Прямоугольные треугольники
Прямоугольные треугольники СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи “Збери” задачу
“Збери” задачу Урок 9 Розв. типових задач
Урок 9 Розв. типових задач Перпендикулярность плоскостей
Перпендикулярность плоскостей Действия с десятичными дробями. Магницкий Леонтий Филиппович
Действия с десятичными дробями. Магницкий Леонтий Филиппович Геометрический смысл производной
Геометрический смысл производной Презентация на тему Формулы
Презентация на тему Формулы  Золотое сечение
Золотое сечение Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Некоторые ошибки интерпретации относительных величин
Некоторые ошибки интерпретации относительных величин Решение задач
Решение задач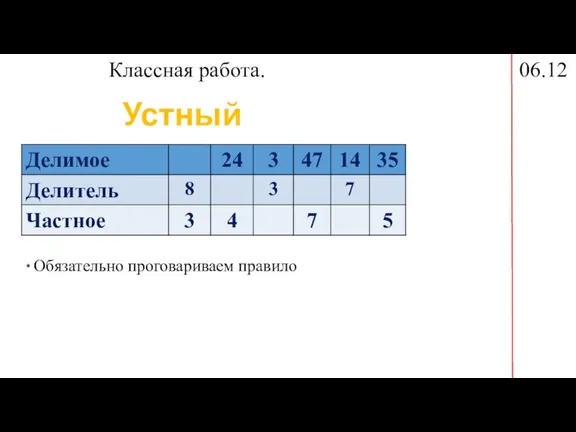 Умножение числа на 1
Умножение числа на 1