Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве

Что изучает стереометрия ?
Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления.
Стереометрия дает метод научного познания, способствует развитию логического мышления.
Стереометрия – сама по себе очень интересна. Она имеет яркую историю, связанную с именами знаменитых ученых

"Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет".
Леонардо да Винчи

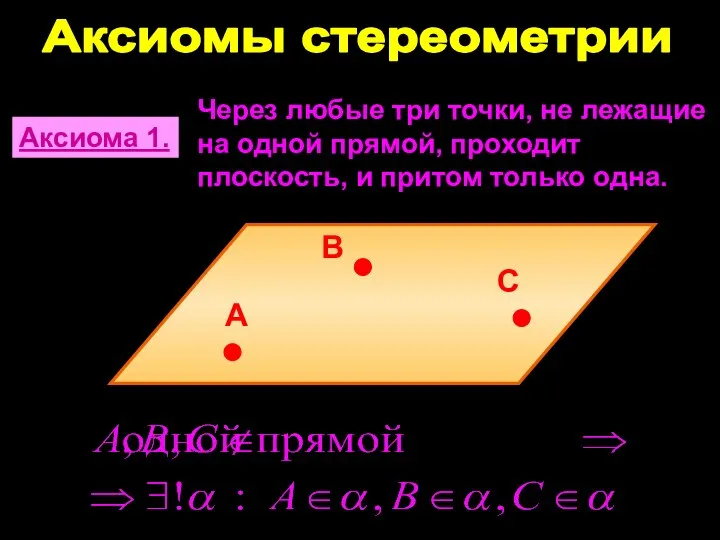
Аксиомы стереометрии
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

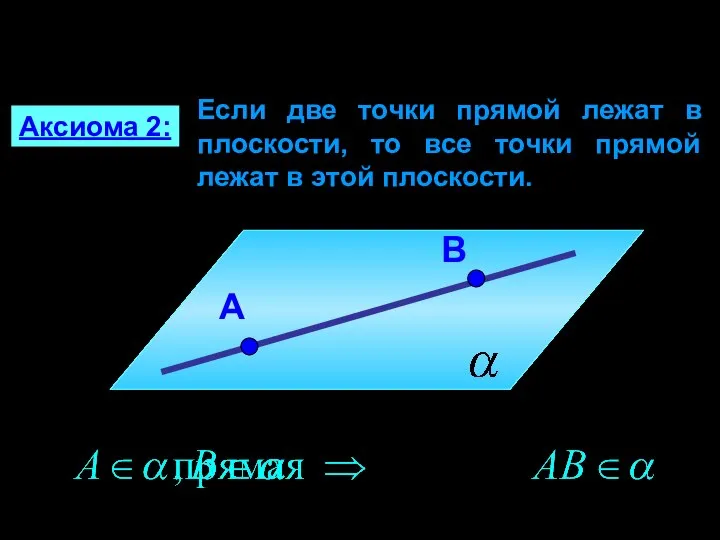
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Аксиома 2:

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Аксиома 3:
В таком случае говорят, что плоскости пересекаются по прямой

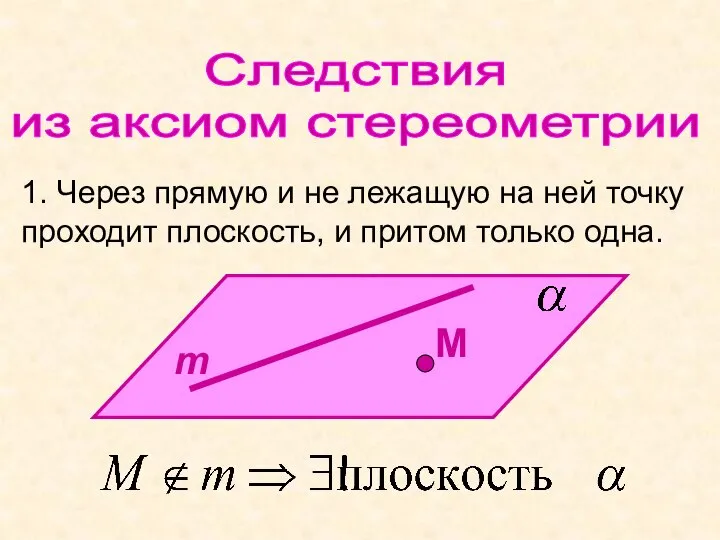
Следствия
из аксиом стереометрии
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

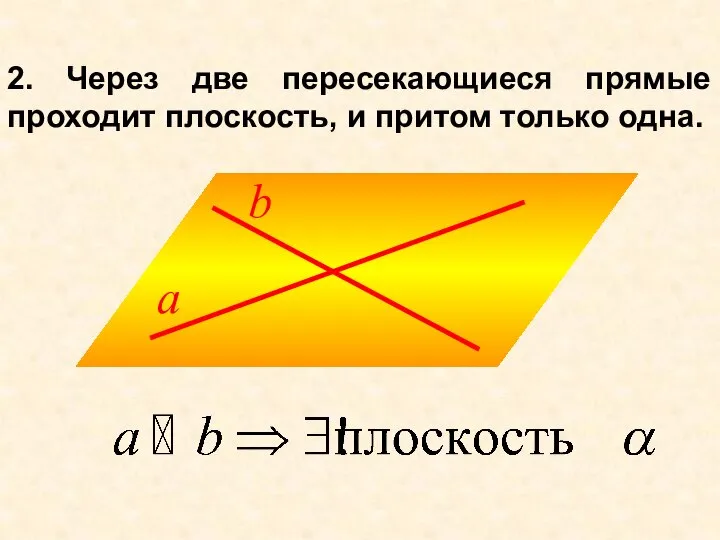
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Взаимное расположение
в пространстве двух прямых
Две прямые лежат в одной плоскости
2. Прямые
пересекаются
1. Прямые
параллельны
Одна общая точка
Нет общих точек

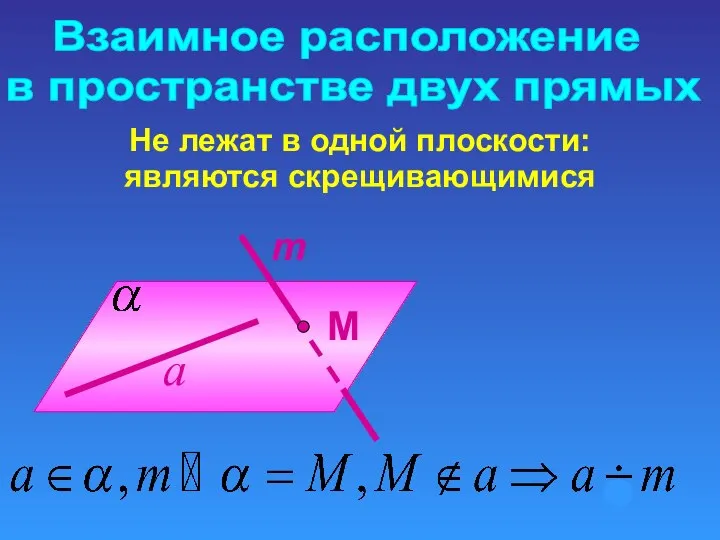
Взаимное расположение
в пространстве двух прямых
Не лежат в одной плоскости:
являются скрещивающимися
m

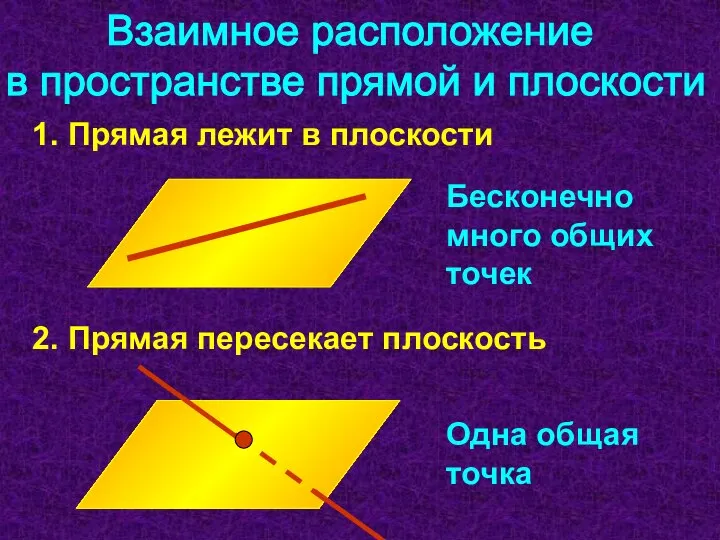
Взаимное расположение
в пространстве прямой и плоскости
1. Прямая лежит в плоскости
2. Прямая пересекает плоскость
Бесконечно много общих точек
Одна общая точка

3. Прямая параллельна плоскости.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Нет общих точек
Признак параллельности прямой и плоскости:

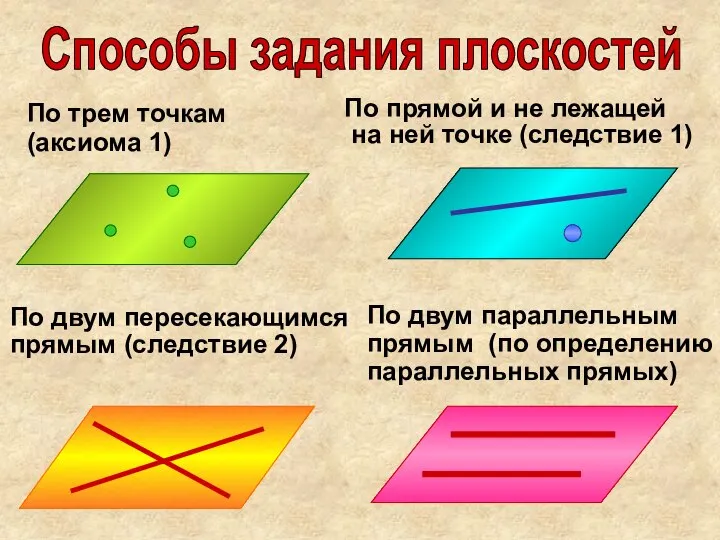
Способы задания плоскостей
По трем точкам
(аксиома 1)
По прямой и не лежащей
на ней точке (следствие 1)
По двум пересекающимся
прямым (следствие 2)
По двум параллельным прямым (по определению параллельных прямых)

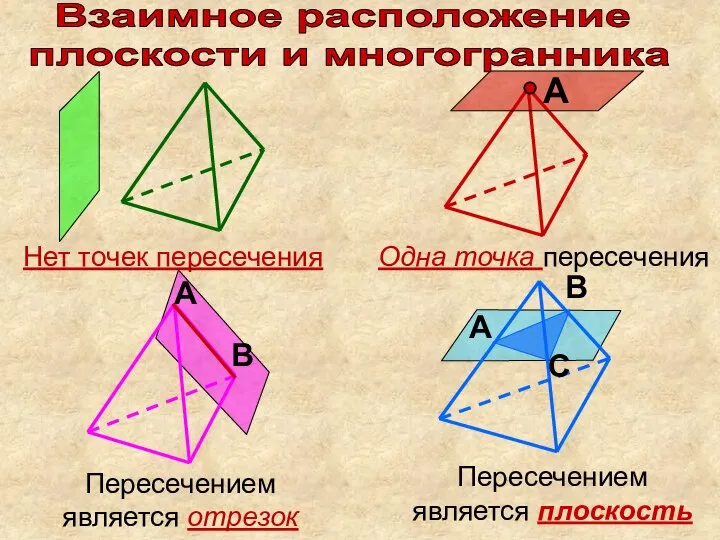
Взаимное расположение
плоскости и многогранника
В
А
Нет точек пересечения
Одна точка пересечения
Пересечением
является отрезок
Пересечением
является плоскость