Содержание
- 2. Цели урока: Рассмотреть понятие предела числовой последовательности Сформировать начальные представления о вычислении пределов числовых последовательностей Продолжить
- 3. Повторение, ответьте на вопросы: Дайте определение числовой последовательности. Какие способы задания числовой последовательности вы знаете? (приведите
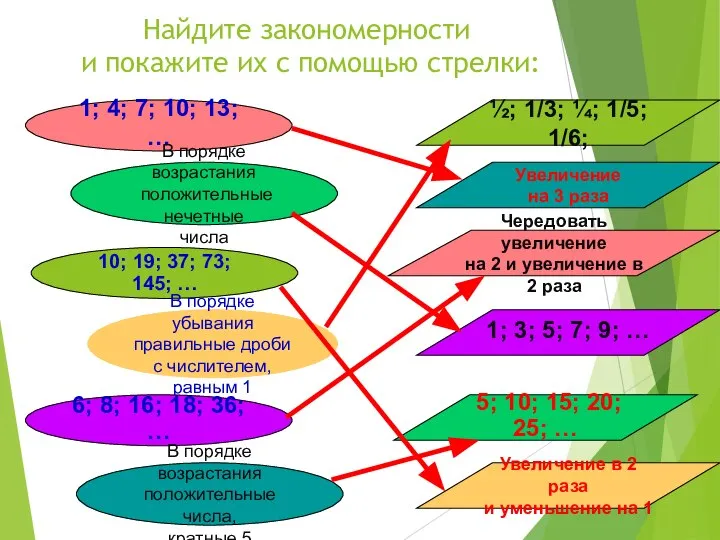
- 4. Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке
- 5. Определение 1 Пусть а – точка прямой, а r – положительное число. Интервал (а-r, а+r) называют
- 6. Укажите окрестность точки а радиуса r в виде интервала, если: а) а = 0 r =
- 7. Окрестностью какой точки и какого радиуса является интервал а = 2 r = 1 а) (1;
- 8. Определение 2 Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b
- 9. Чему равен предел данной последовательности? Вывод: Вывод:
- 10. Свойства 1) Предел суммы равен сумме пределов 2) Предел произведения равен произведению пределов 4) Постоянный множитель
- 11. Рефлексия
- 12. Домашнее задание п.4.3 п.4.4 №4.35 (д-и) 4.36 (в,г)
- 14. Скачать презентацию










 Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Основы системной динамики
Основы системной динамики Логарифмические уравнения. Уравнения, решаемые методом введения новой переменной
Логарифмические уравнения. Уравнения, решаемые методом введения новой переменной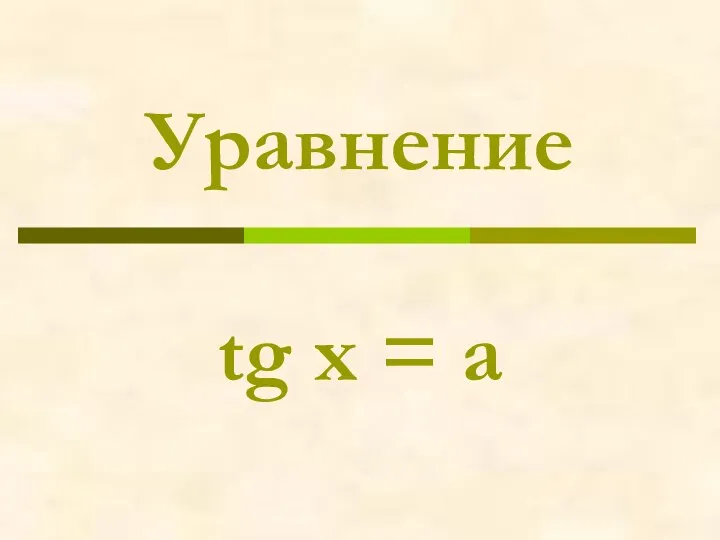 Уравнение tg x = a
Уравнение tg x = a Презентация на тему Смежные и вертикальные углы
Презентация на тему Смежные и вертикальные углы  Роль семьи в развитии речи ребенка
Роль семьи в развитии речи ребенка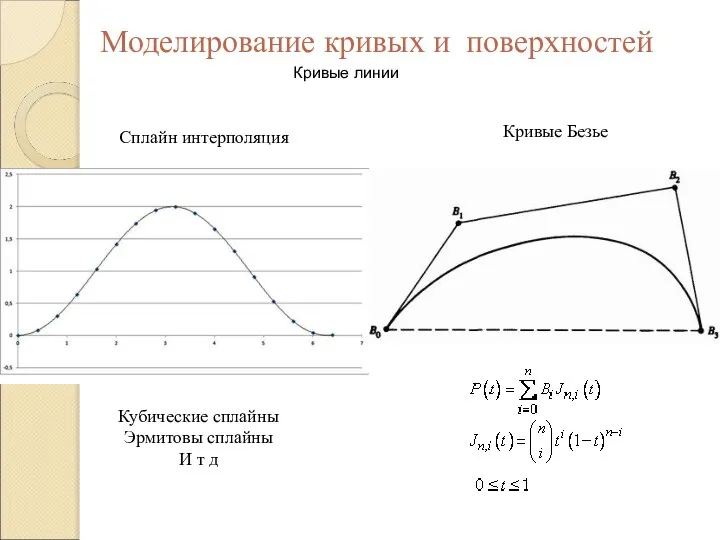 Моделирование кривых и поверхностей
Моделирование кривых и поверхностей Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной Объем конуса
Объем конуса Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Математическое моделирование
Математическое моделирование Решение задач
Решение задач Числовые ряды, основные определения и свойства
Числовые ряды, основные определения и свойства Проверочная работа по теме Кровь
Проверочная работа по теме Кровь Свойства тригонометрических функций
Свойства тригонометрических функций УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н.
УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н. Математическое и программное обеспечение многопользовательских тренажеров с погружением в иммерсивные виртуальные среды
Математическое и программное обеспечение многопользовательских тренажеров с погружением в иммерсивные виртуальные среды Урок – творческий проект по математике Мастерская игрушек
Урок – творческий проект по математике Мастерская игрушек Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Старинные меры веса 1 класс - Презентация по математике_
Старинные меры веса 1 класс - Презентация по математике_ Теплицы
Теплицы Пропорциональные отрезки в прямоугольном треугольнике (8 класс)
Пропорциональные отрезки в прямоугольном треугольнике (8 класс) Засели числовые домики
Засели числовые домики Уравнения с одной переменной
Уравнения с одной переменной Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Увеличение и уменьшение в одно и то же число раз
Увеличение и уменьшение в одно и то же число раз النشاط الثالث
النشاط الثالث О математическом языке
О математическом языке