Свойства равнобедренного треугольника

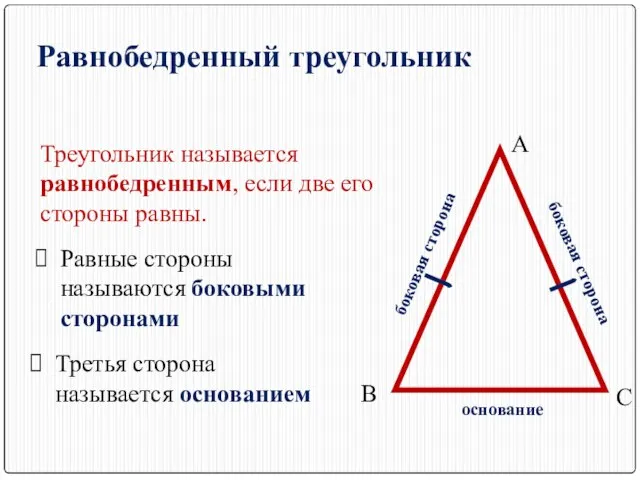
Равнобедренный треугольник
Треугольник называется равнобедренным, если две его стороны равны.
А
В
С
Равные стороны называются боковыми сторонами
боковая сторона
боковая сторона
Третья сторона называется основанием
основание

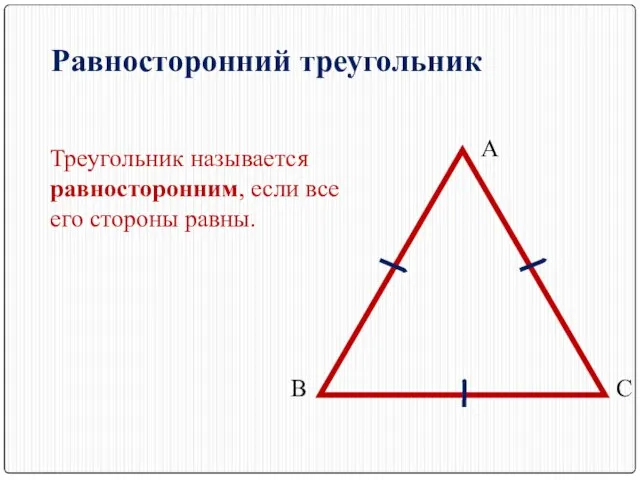
Равносторонний треугольник
Треугольник называется равносторонним, если все его стороны равны.
А
В
С

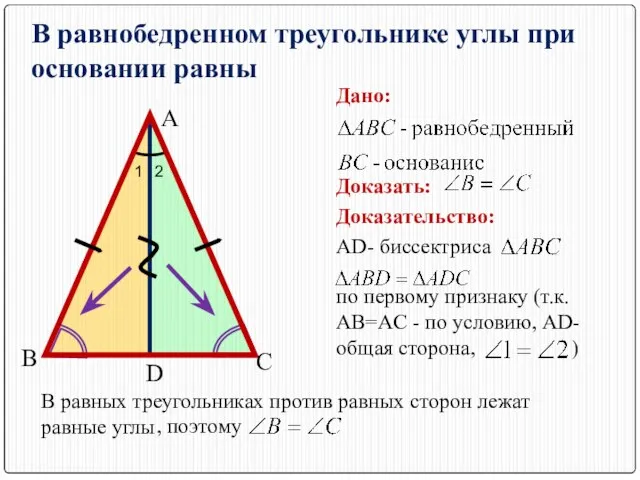
В равнобедренном треугольнике углы при основании равны
А
В
С
Дано:
Доказать:
D
Доказательство:
AD- биссектриса
по первому признаку (т.к. AB=AC - по условию, AD-общая сторона, )
В равных треугольниках против равных сторон лежат равные углы
, поэтому
1
2

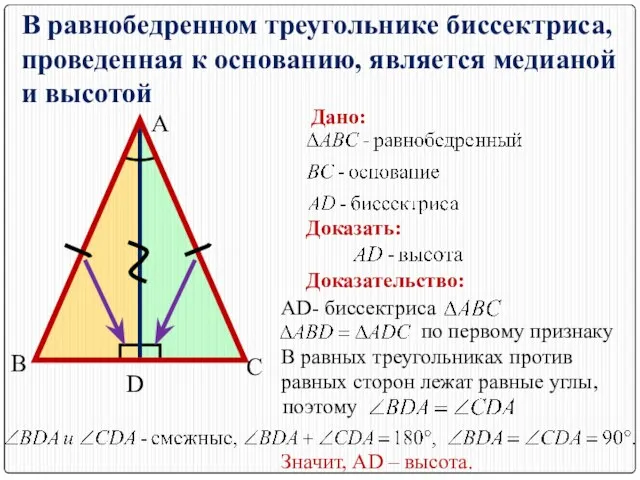
В равных треугольниках против равных углов лежат равные стороны
, поэтому BD=DC.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
А
В
С
Дано:
Доказать:
D
Доказательство:
AD- биссектриса
по первому признаку
Значит, AD - медиана

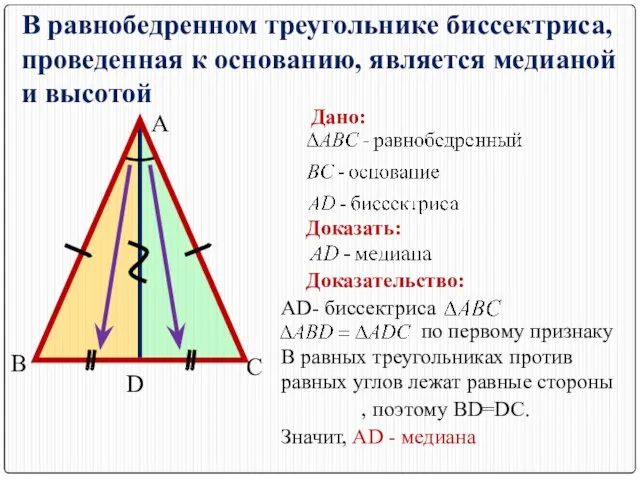
В равных треугольниках против равных сторон лежат равные углы,
поэтому
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
А
В
С
Дано:
Доказать:
D
Доказательство:
AD- биссектриса
по первому признаку
Значит, AD – высота.

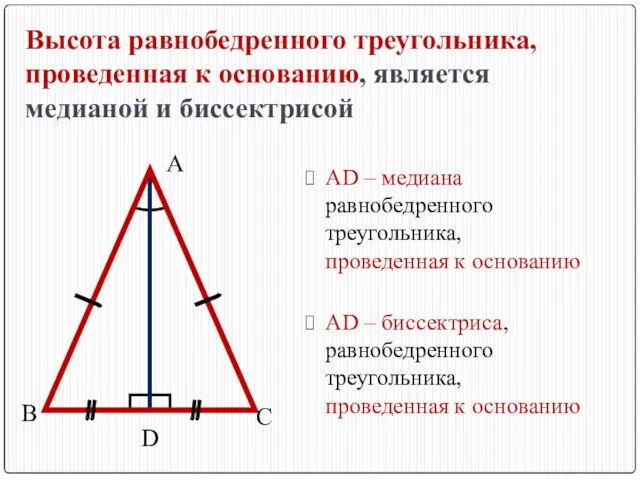
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой
В
С
D
А
AD – биссектриса, равнобедренного треугольника,
проведенная к основанию
AD – медиана равнобедренного треугольника,
проведенная к основанию

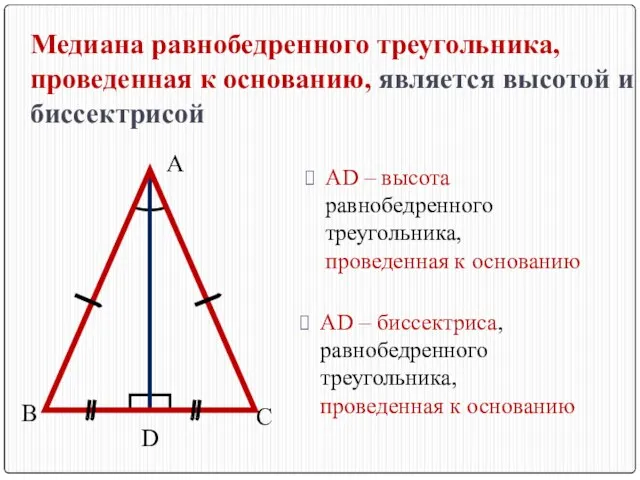
В
С
D
А
AD – биссектриса, равнобедренного треугольника,
проведенная к основанию
AD – высота равнобедренного треугольника,
проведенная к основанию
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой

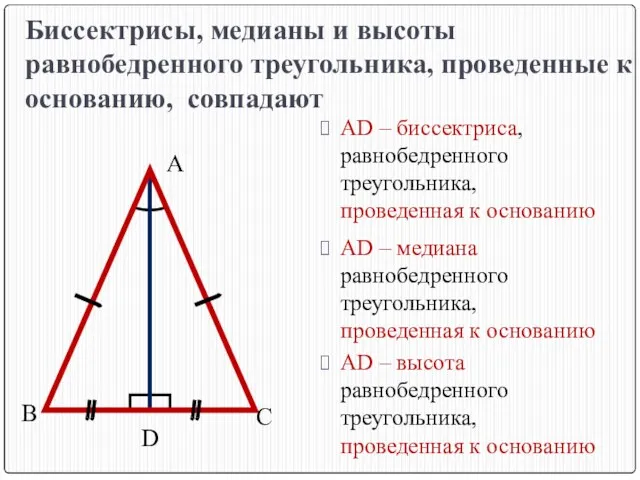
Биссектрисы, медианы и высоты равнобедренного треугольника, проведенные к основанию, совпадают
AD – биссектриса, равнобедренного треугольника,
проведенная к основанию
В
С
А
D
AD – медиана равнобедренного треугольника,
проведенная к основанию
AD – высота равнобедренного треугольника,
проведенная к основанию

Найдите ∟ВСА

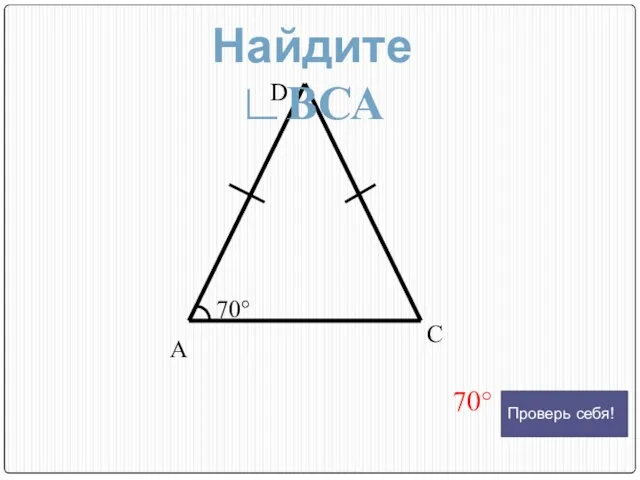
А
D
С
70°
70°
Найдите ∟ВСА

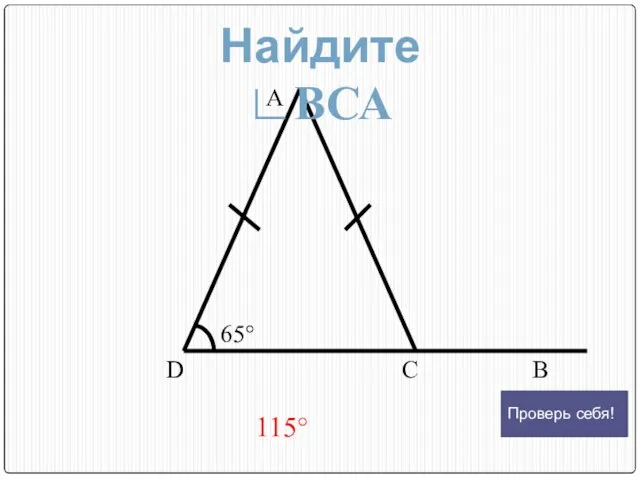
А
D
С
В
65°
115°
Найдите ∟ВСА

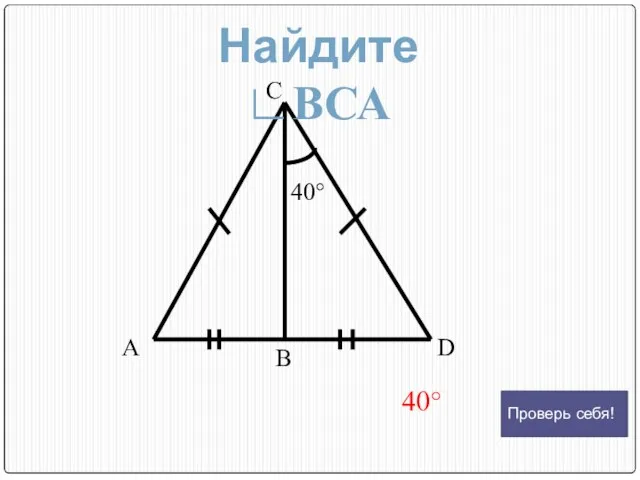
С
А
В
D
40°
40°
Найдите ∟ВСА

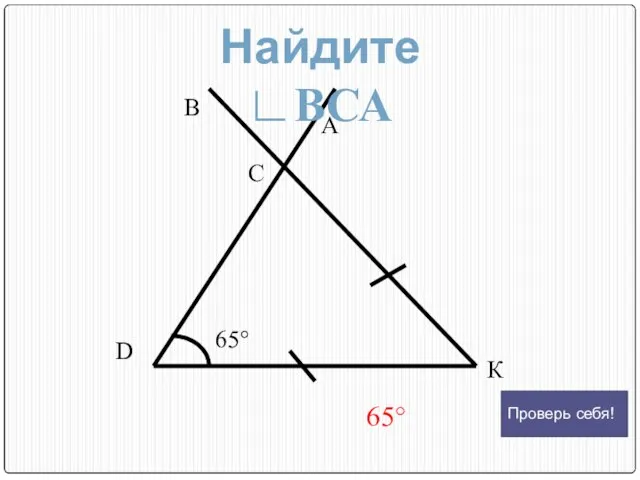
В
С
А
65°
D
К
65°
Найдите ∟ВСА

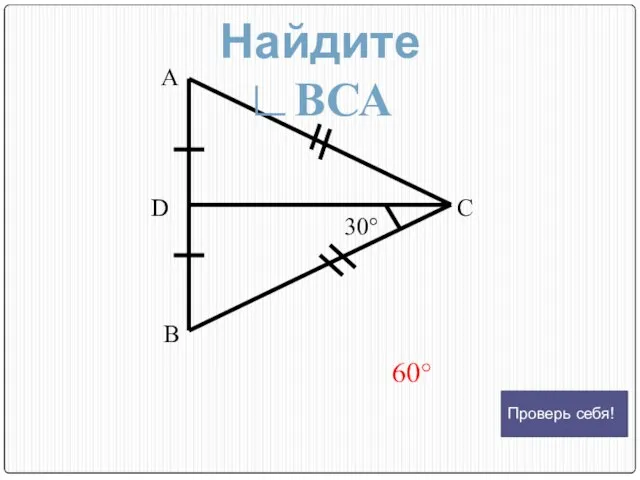
А
С
D
В
30°
60°
Найдите ∟ВСА

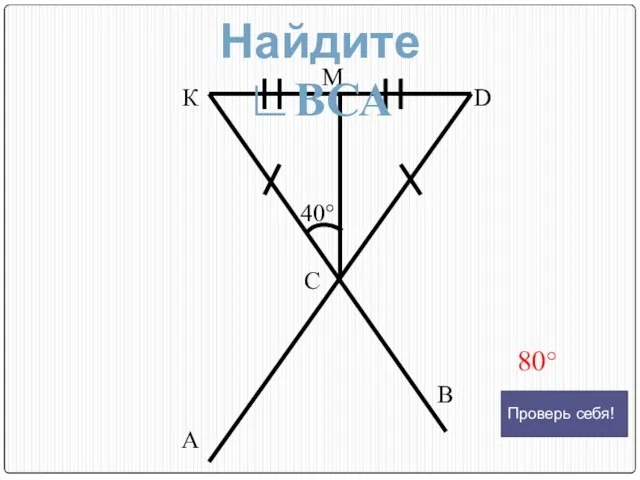
К
М
D
С
А
В
40°
80°
Найдите ∟ВСА

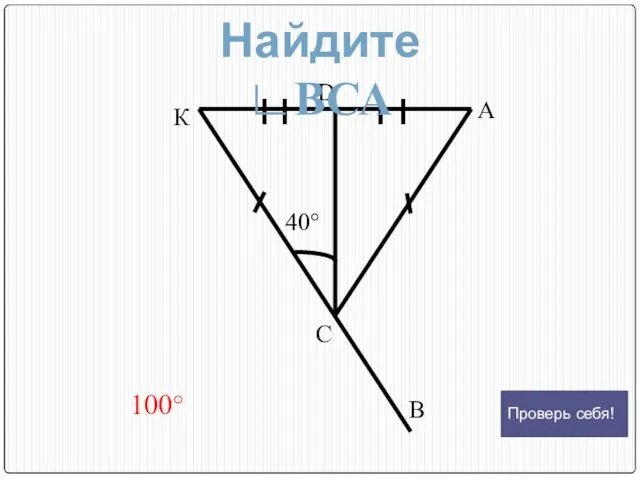
К
D
А
С
В
100°
40°
Найдите ∟ВСА

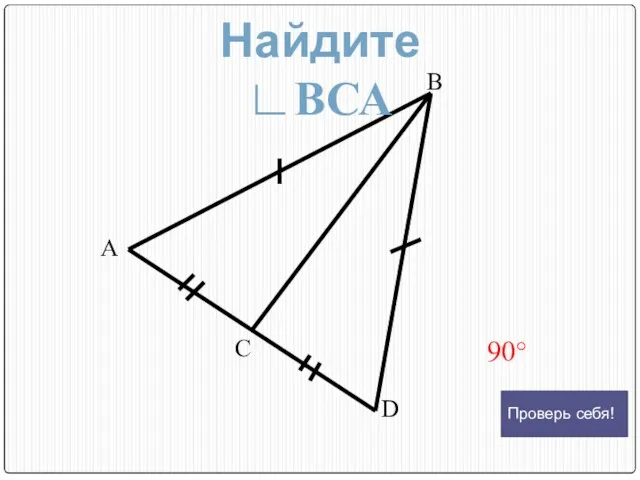
В
А
С
D
90°
Найдите ∟ВСА

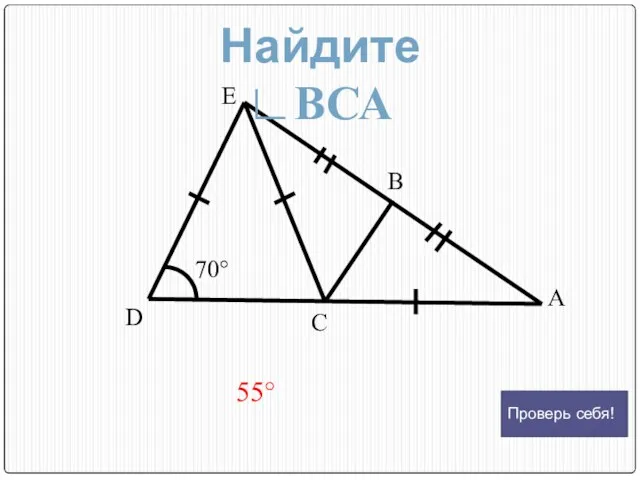
Е
D
С
В
А
70°
55°
Найдите ∟ВСА

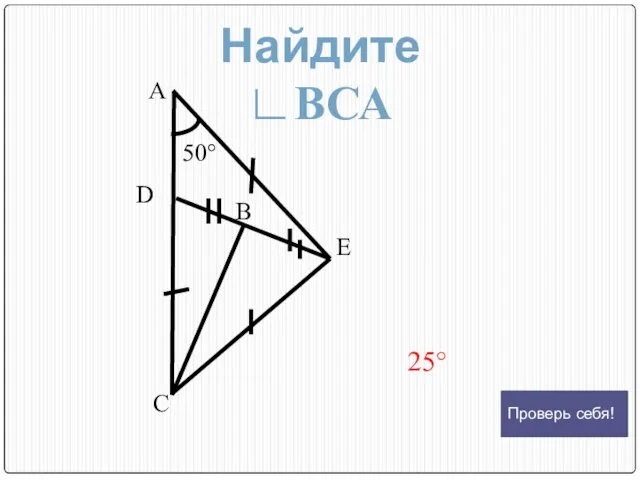
А
D
С
В
Е
50°
25°
Найдите ∟ВСА