Содержание
- 2. Цели и задачи организация причинных подмножеств пространственно-временных многообразий в алгебраические структуры (решетки [1]); изучение свойств полученных
- 3. Решетки (алгебраические системы). Определение Решеткой называется множество с двумя введенными на нем операциями такими, что выполняются
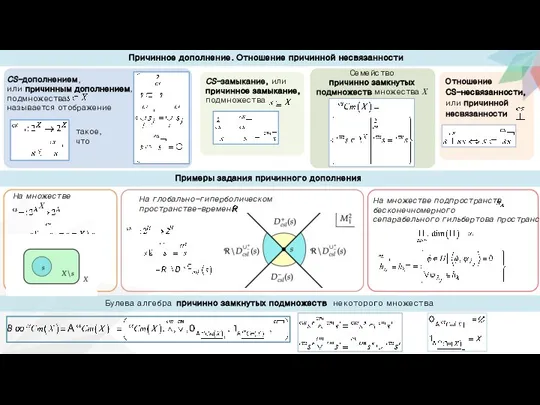
- 4. Булева алгебра причинно замкнутых подмножеств некоторого множества Причинное дополнение. Отношение причинной несвязанности Примеры задания причинного дополнения
- 5. Решетка причинно замкнутых подмножеств Квантовомеханические решетки Классические решетки 2. Решетки диамантов на 1. Решетки конусов на
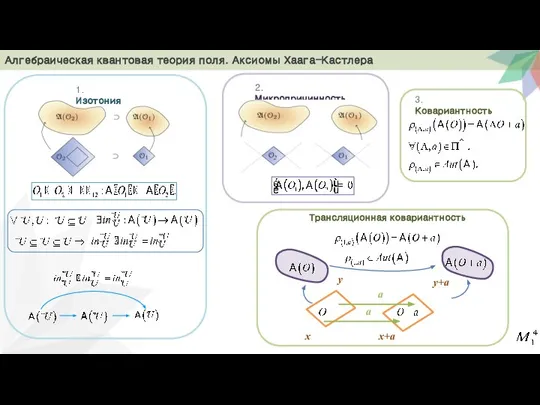
- 6. Алгебраическая квантовая теория поля. Аксиомы Хаага-Кастлера 1. Изотония 2. Микропричинность 3. Ковариантность Трансляционная ковариантность
- 7. 5. Спектральное условие Локально ковариантная квантовая теория поля [5] Алгебраическая квантовая теория поля. Аксиомы Хаага-Кастлера [5]
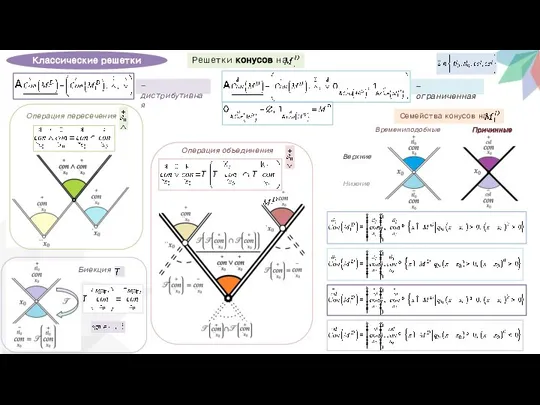
- 8. Классические решетки Решетки конусов на -дистрибутивная -ограниченная Операция пересечения Биекция Операция объединения Семейства конусов на Верхние
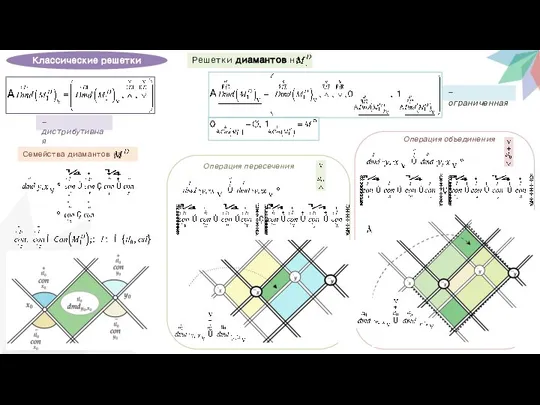
- 9. Классические решетки -дистрибутивная -ограниченная Операция объединения
- 10. Классические решетки Примеры
- 11. Квантовомеханические решетки 3. Ограниченная решетка с дополнениями алгебр фон Нойманна 1. Ограниченная решетка с ортодополнениями замкнутых
- 12. Заключение Построение алгебраических структур, индуцированных отношением причинности, в данной работе ограничивается решетками Как семейства подлежащих подмножеств,
- 13. Апробация работы 1. Выступления на «Семинаре по алгебре, геометрии в математической физике» (руководитель: Никифоров А.М.) 2.
- 15. Скачать презентацию



![5. Спектральное условие Локально ковариантная квантовая теория поля [5] Алгебраическая квантовая теория](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1038465/slide-6.jpg)




 Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс)
Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс) Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс Сложение с переходом через десяток вида +6, +7. Считаем с гномами
Сложение с переходом через десяток вида +6, +7. Считаем с гномами Сложные проценты. Контрольная
Сложные проценты. Контрольная Решение квадратных уравнений
Решение квадратных уравнений Скалярное произведение векторов. Решение задач
Скалярное произведение векторов. Решение задач Вклад Гаусса в развитии теории комплексных чисел
Вклад Гаусса в развитии теории комплексных чисел Расчет нормированных приоритетов
Расчет нормированных приоритетов Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Объёмные фигуры и формулы нахождения объёма
Объёмные фигуры и формулы нахождения объёма Презентация на тему: Турнир смекалистых
Презентация на тему: Турнир смекалистых Понятие математической индукции и ее применение
Понятие математической индукции и ее применение Итоги пробного ОГЭ от 27.02.2021. Разбор варианта №1
Итоги пробного ОГЭ от 27.02.2021. Разбор варианта №1 Длина окружности и число пи
Длина окружности и число пи Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии На оптимизацию с решением
На оптимизацию с решением Комбинаторная задача с монетами
Комбинаторная задача с монетами Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Интересные факты про математику
Интересные факты про математику Умножение и деление смешанных дробей
Умножение и деление смешанных дробей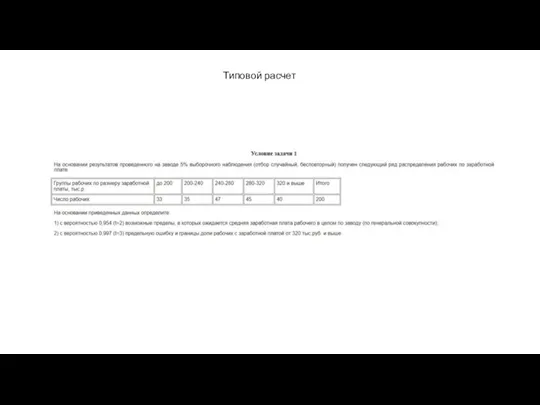 Типовой расчет. Часть 1
Типовой расчет. Часть 1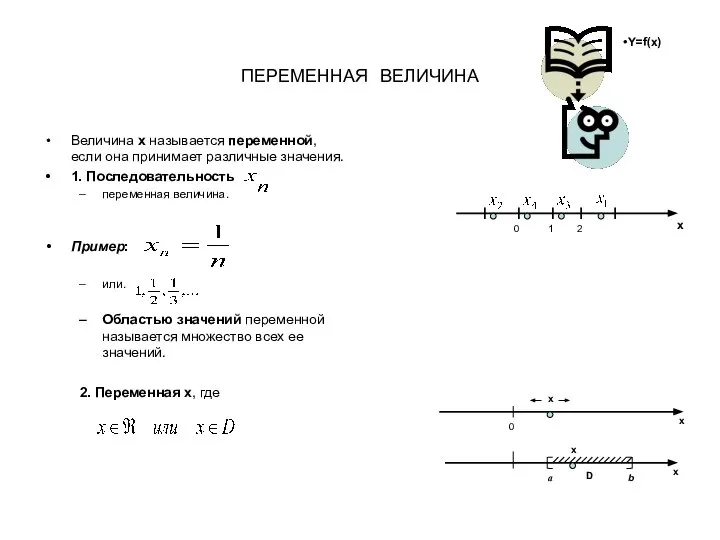 Переменная величина
Переменная величина Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс)
Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс) Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Нахождение угла между прямой и плоскостью
Нахождение угла между прямой и плоскостью Задача о Покупке фруктов
Задача о Покупке фруктов Презентация на тему Тренажер по математике 2 класс
Презентация на тему Тренажер по математике 2 класс