Содержание
- 2. Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени. Показательное уравнение сводится к
- 3. Пример 1.
- 4. 2. Чтобы привести уравнение к виду (1) необходимо в левой части уравнения вынести за скобки общий
- 5. Пример 2.
- 6. 3. Можно разделить обе части уравнения на выражение, не равное нулю
- 7. Пример 3.
- 8. 4. Некоторые показательные уравнения заменой сводятся к квадратным. Надо помнить, что t>0, так как показательная функция
- 9. Пример 4.
- 10. Алгоритм решения показательных уравнений 1. Уравниваем основания степеней во всех слагаемых, содержащих неизвестное в показателе степени.
- 11. Графическое решение уравнения сводится к построению графиков функций левой и правой частей уравнения, нахождению по рисунку
- 13. Скачать презентацию










 Уравнения и неравенства с модулем
Уравнения и неравенства с модулем Физический и геометрический смысл производной
Физический и геометрический смысл производной Арксинус, Арккосинус, Арктангенс, Арккотангенс
Арксинус, Арккосинус, Арктангенс, Арккотангенс Асимптоты функции
Асимптоты функции Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Симметрия и асимметрия
Симметрия и асимметрия Буквенные выражения. Подготовка к контрольной работе
Буквенные выражения. Подготовка к контрольной работе Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Геометрия. Решение задач
Геометрия. Решение задач Плошадь многоугольников
Плошадь многоугольников Размещения
Размещения Метод группировки
Метод группировки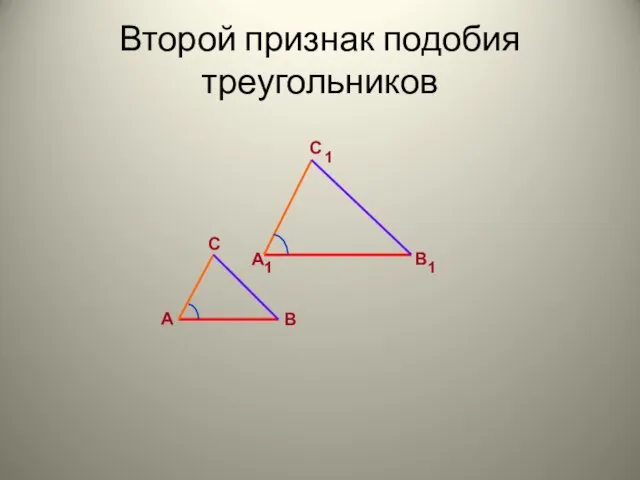 Второй признак подобия треугольников
Второй признак подобия треугольников Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Обзор приложений копул к задачам Байесовской классификации при машинном обучении
Обзор приложений копул к задачам Байесовской классификации при машинном обучении Состав числа 7. Головоломка Корова
Состав числа 7. Головоломка Корова Арифметический корень степени n
Арифметический корень степени n Как умножали египтяне
Как умножали египтяне Решение примеров на сложение в пределах 20. (1-2 класс)
Решение примеров на сложение в пределах 20. (1-2 класс) Математика. Закрепление изученного материала. 4 класс
Математика. Закрепление изученного материала. 4 класс Системы показательных уравнений и неравенств
Системы показательных уравнений и неравенств Подготовка к контрольной работе за полугодие
Подготовка к контрольной работе за полугодие Плоскости
Плоскости Кратные чисел. 5 класс
Кратные чисел. 5 класс Практика. Дискретная математика
Практика. Дискретная математика Случайные величины. Тема 3. Часть
Случайные величины. Тема 3. Часть Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение
Обыкновенные дифференциальные уравнения первого порядка. Классификация и решение Презентация на тему Приближённые вычисления
Презентация на тему Приближённые вычисления