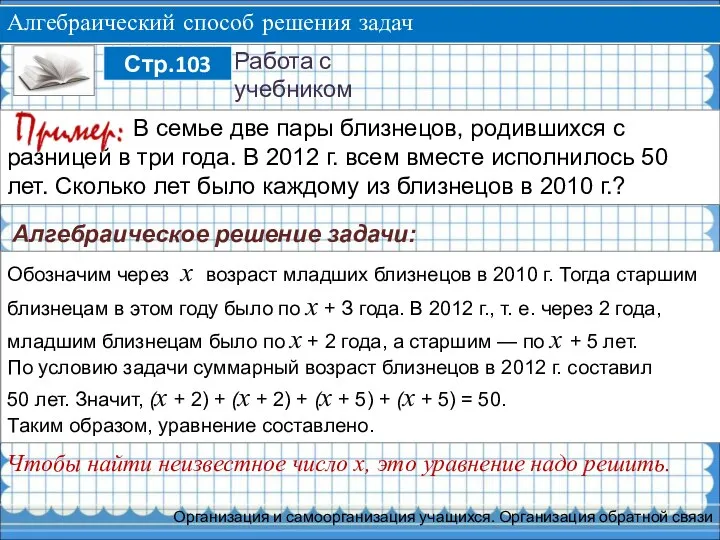
этом году было по x + З года. В 2012 г., т. е. через 2 года, младшим близнецам было по x + 2 года, а старшим — по x + 5 лет.
По условию задачи суммарный возраст близнецов в 2012 г. составил
50 лет. Значит, (х + 2) + (х + 2) + (х + 5) + (х + 5) = 50.
Таким образом, уравнение составлено.
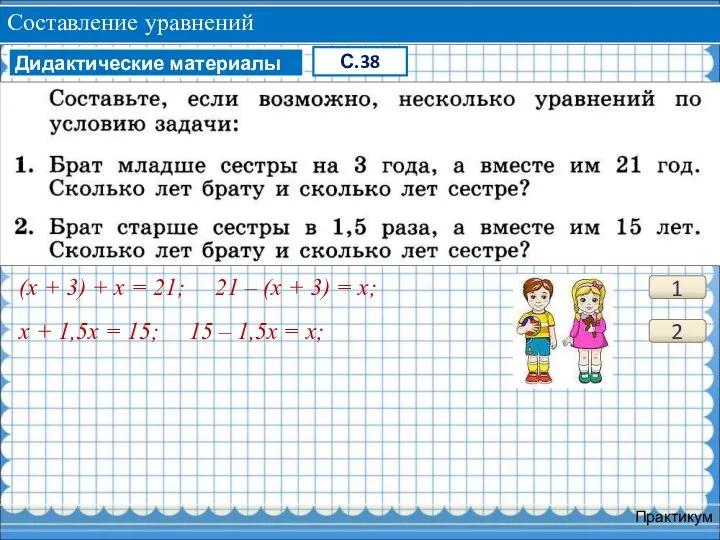
В семье две пары близнецов, родившихся с разницей в три года. В 2012 г. всем вместе исполнилось 50 лет. Сколько лет было каждому из близнецов в 2010 г.?
Алгебраический способ решения задач
Организация и самоорганизация учащихся. Организация обратной связи
Алгебраическое решение задачи:
Чтобы найти неизвестное число х, это уравнение надо решить.







 Задания на развитие логики
Задания на развитие логики Тригонометрические уравнения, приводимые к квадратным
Тригонометрические уравнения, приводимые к квадратным Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Системы линейных алгебраических уравнений. Лекция 1
Системы линейных алгебраических уравнений. Лекция 1 Треугольники
Треугольники Куб. Параллелепипед. Тест
Куб. Параллелепипед. Тест Удивительная симметрия
Удивительная симметрия Сравнение чисел. 1 класс
Сравнение чисел. 1 класс В мире математики
В мире математики Пересекающиеся прямые
Пересекающиеся прямые Кенгуру – математика для всех
Кенгуру – математика для всех Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Парная регрессия и корреляция
Парная регрессия и корреляция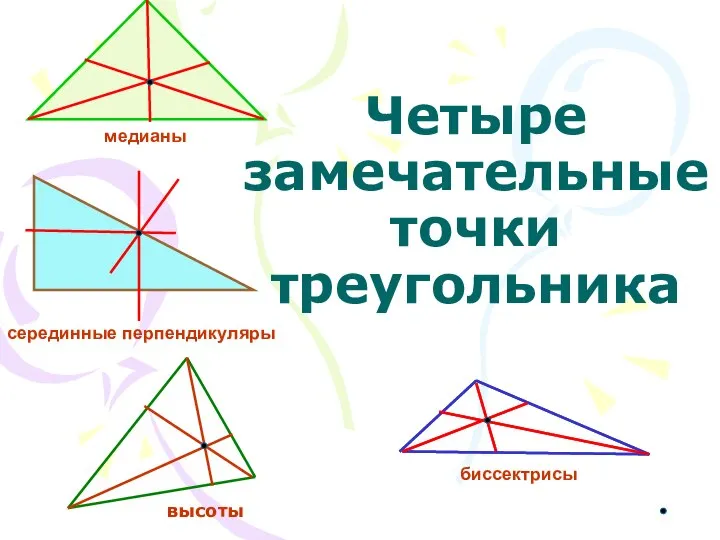 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Математика. Раздел 6. Метод координат в пространстве. Занятие 66. Уравнение плоскости
Математика. Раздел 6. Метод координат в пространстве. Занятие 66. Уравнение плоскости Перестановки. Размещения
Перестановки. Размещения Вычисление определителя третьего порядка по правилу треугольников
Вычисление определителя третьего порядка по правилу треугольников Эконометрика. Семинар 2. Решение задачи 4
Эконометрика. Семинар 2. Решение задачи 4 Множества
Множества Дроби
Дроби Первые единицы измерения длины. 1 класс
Первые единицы измерения длины. 1 класс Algebraic constructions generated by causal structure of space-times
Algebraic constructions generated by causal structure of space-times Пивкин ИКС-34 (2)
Пивкин ИКС-34 (2) Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Загадки и тайны треугольника
Загадки и тайны треугольника Аксиомы стереометрии
Аксиомы стереометрии Разложение определителя. Нахождение обратной матрицы
Разложение определителя. Нахождение обратной матрицы