- Главная
- Математика
- Числовая окружность

Содержание
Слайд 2Если R = 1, то L = 2π
0
2π
-π
0
-2π
π
Против часовой стрелки -
положительный обход
По
Если R = 1, то L = 2π
0
2π
-π
0
-2π
π
Против часовой стрелки -
положительный обход
По
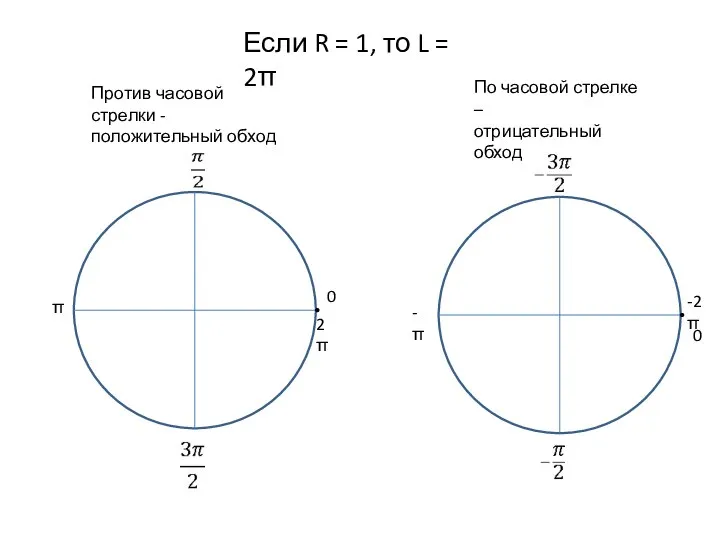
часовой стрелке –
отрицательный обход
отрицательный обход
Слайд 30
2π
π
3π
4π
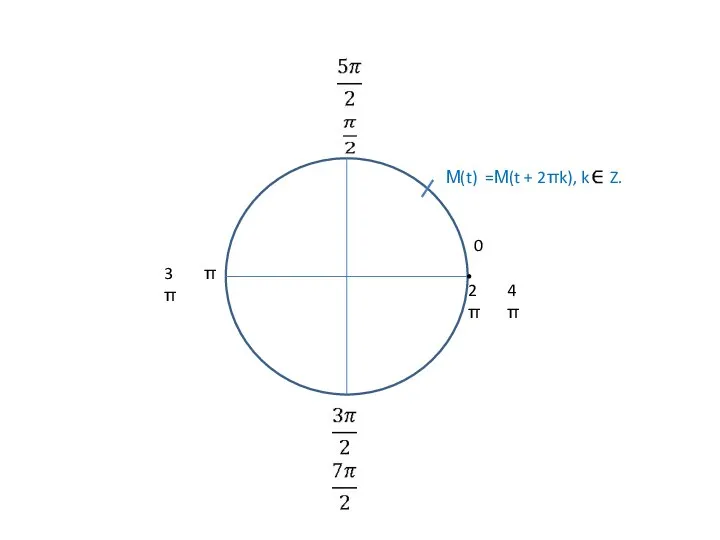
М(t)
=М(t + 2πk), k Z.
0
2π
π
3π
4π
М(t)
=М(t + 2πk), k Z.
Слайд 40
2π
π
0
2π
π
Первый макет
Второй макет
Каждая из четвертей числовой окружности разделена на две равных части
Каждая
0
2π
π
0
2π
π
Первый макет
Второй макет
Каждая из четвертей числовой окружности разделена на две равных части
Каждая
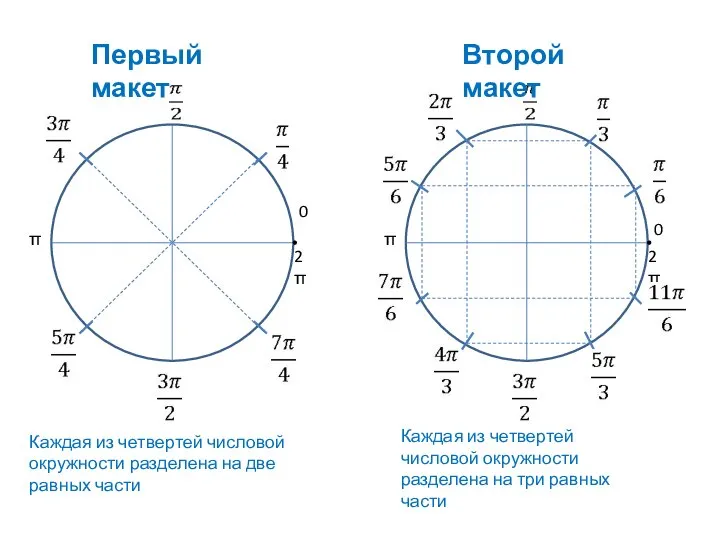
из четвертей числовой окружности разделена на три равных части
Следующая -
Акустичне явище грім Теорема Пифагора и способы ее доказательства
Теорема Пифагора и способы ее доказательства Движение. Виды движения
Движение. Виды движения Формула Бернулли
Формула Бернулли Решение геометрических задач. Треугольники
Решение геометрических задач. Треугольники Окружность и круг
Окружность и круг Правильные многогранники
Правильные многогранники Сказ о дележе наследства (задача)
Сказ о дележе наследства (задача) Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов
Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов Решение задачи Корабли или история 7 семестров
Решение задачи Корабли или история 7 семестров Функция у=arccos x
Функция у=arccos x Неопределённый интеграл. Элементы интегрального исчисления
Неопределённый интеграл. Элементы интегрального исчисления Алгебра логики при решении практических задач
Алгебра логики при решении практических задач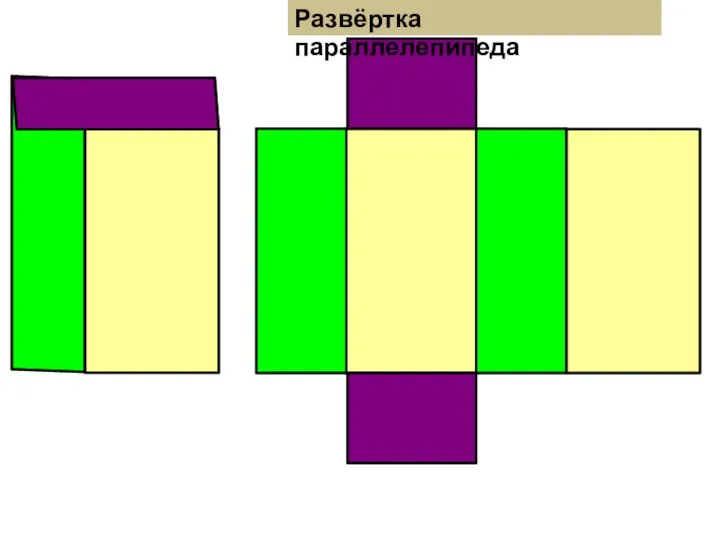 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Задача на арифметическую прогрессию. 9 класс
Задача на арифметическую прогрессию. 9 класс Решение задач
Решение задач Геометрический смысл производной. Уравнение касательной
Геометрический смысл производной. Уравнение касательной Формулы для решения задач по шуму
Формулы для решения задач по шуму РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания
РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания Таблица умножения на 3 в стихах
Таблица умножения на 3 в стихах Правильные многоугольники в природе и в жизни
Правильные многоугольники в природе и в жизни Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр
Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Скалярное произведение векторов
Скалярное произведение векторов Задача
Задача Конструктор (1)
Конструктор (1) Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным ВПР - 7- 9 класс
ВПР - 7- 9 класс Личные местоимения
Личные местоимения