Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр

ЗАДАЧА
На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М и боковую сторону СВ в точке N. Найдите периметр треугольника MNC, если АВ = 10, АС = 8.

РЕШЕНИЕ.
(свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр, свойство отрезков секущих, теорема Пифагора).
Способ I

1. Найдем сторону СМ треугольника MNC.
2. Найдем сторону СN треугольника MNC. Это можно сделать несколькими способами.
Способ I

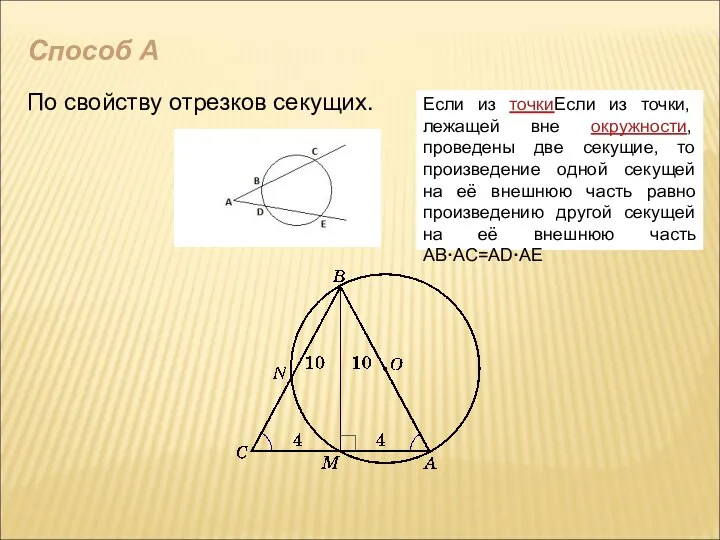
Способ А
По свойству отрезков секущих.
Если из точкиЕсли из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть АВ·АС=АD·АЕ

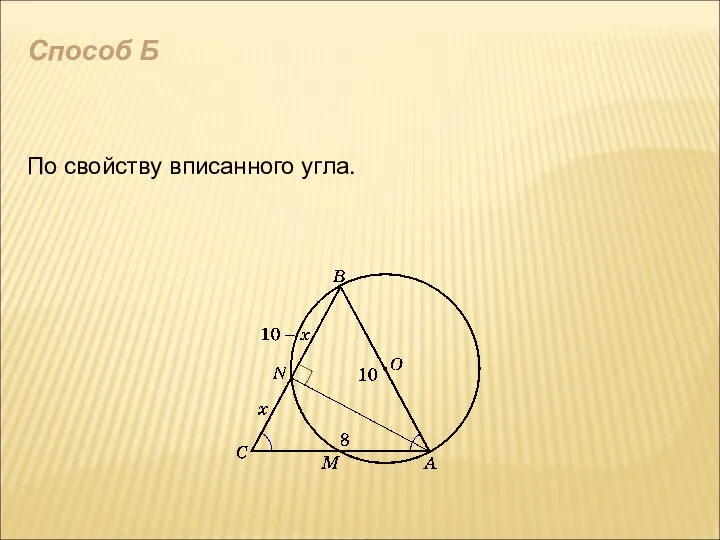
Способ Б
По свойству вписанного угла.

Способ В
С помощью теоремы Пифагора.

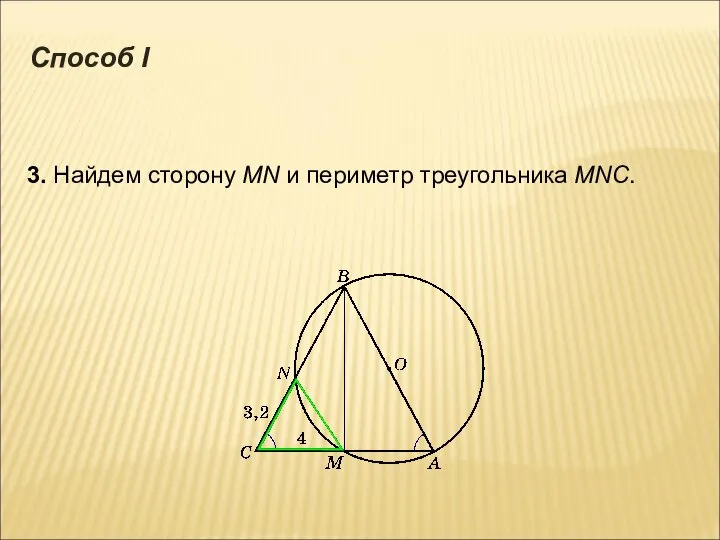
3. Найдем сторону МN и периметр треугольника MNC.
Способ I

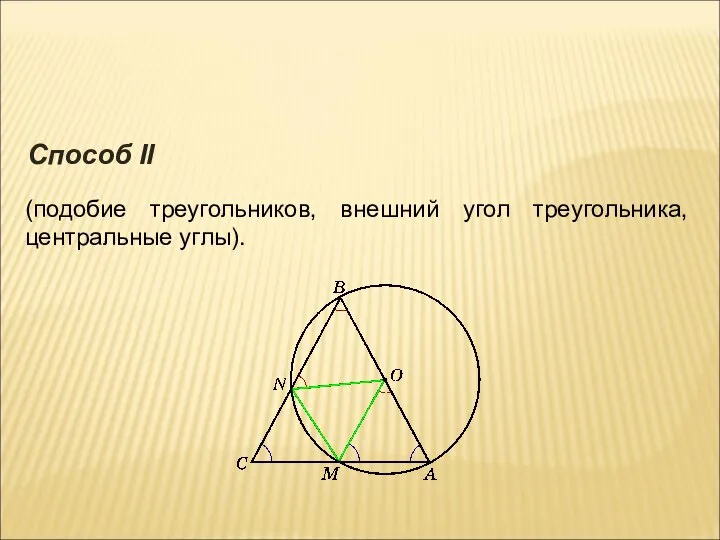
(подобие треугольников, внешний угол треугольника, центральные углы).
Способ II