Алгоритм расчета аппроксимирующей функции I-интеграла и L-интеграла

1 – записываются моменты времени существующего временного ряда
[tн,tк[ t1, t2, t3…tк
2 – записываются значения ординаты временного ряда
у1, у2, у3…ук
3 – вычисляются определения
t1y1, t2y2, t3y3… tnyn
4 – вычисляются площади, т.к. интеграл - это сумма площадей под кривой
S(t1), S(t2), S(t3)… S(tn) S(ti)=0.5(ti-ti-1)[y(ti)+y(ti-1)]
При этом следует учитывать, что при вычислении площади S(ti) требуется значение временного сигнала в момент времени t0 . Данное значение можно взять равным 0,5у1 .
5 – определяется нарастающая сумма площадей
S(t1), S(t1)+ S(t2)… ∑Si (i=1…n)
Это и есть оценка интеграла.
6 – производится оценка L-интеграла
L(tm)=tmy(tm)+∑Si (i=1…m), где m

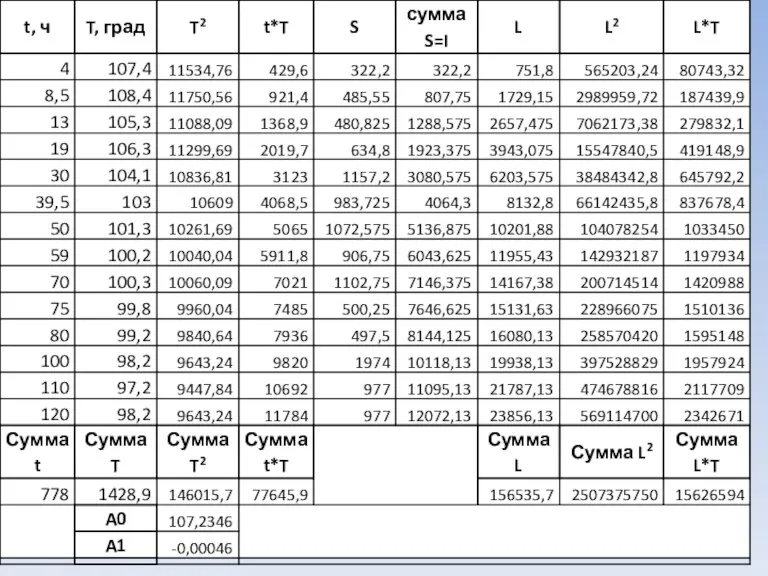
7 – вычисляются параметры a0 и а1 по методу наименьших квадратов
8 – определяется коэффициент корреляции

Пример
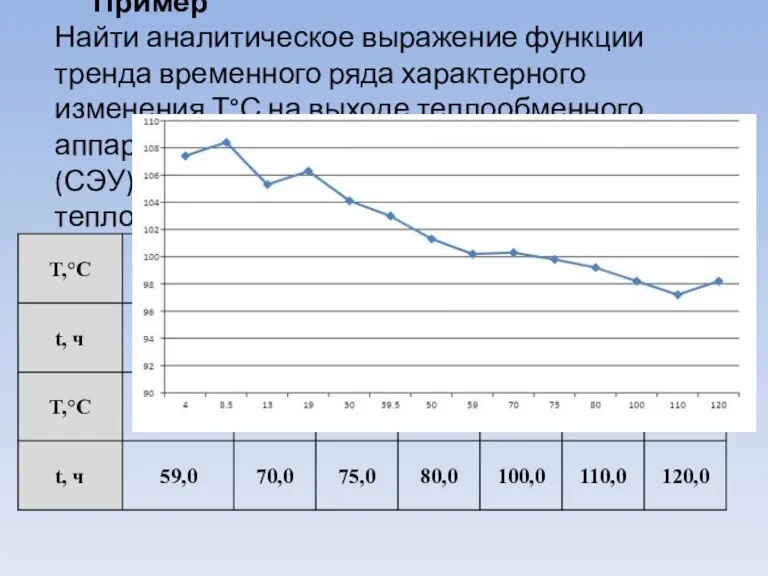
Найти аналитическое выражение функции тренда временного ряда характерного изменения Т°С на выходе теплообменного аппарата судовой энергетической установки (СЭУ) в следствие нарастающего засоления тепловых труб.