Содержание
- 2. Цели урока: Ввести понятие степенной функции Построить графики степенной функции? Сдвиг графика вдоль осей координат. -Рассмотреть
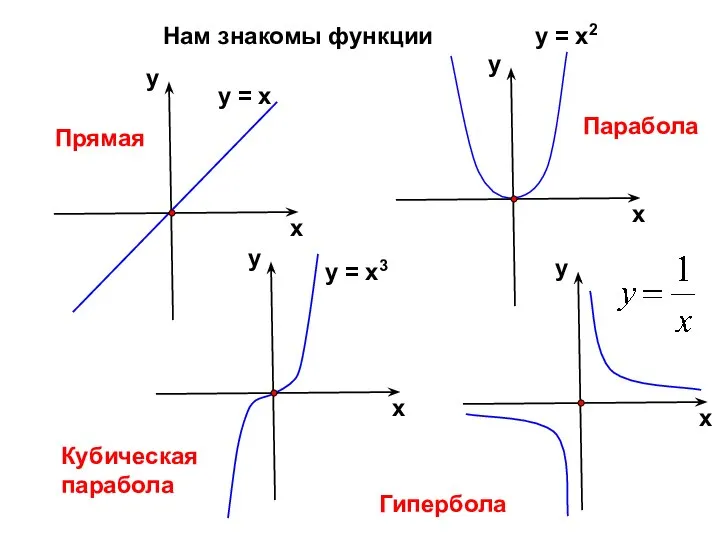
- 4. Нам знакомы функции Прямая Парабола Кубическая парабола Гипербола
- 5. Все эти функции являются частными случаями степенной функции у = хr, где r – заданное действительное
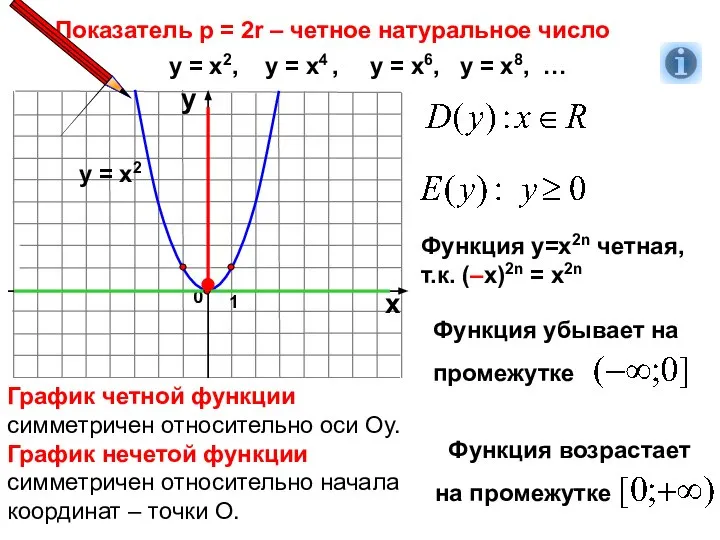
- 6. Показатель р = 2r – четное натуральное число 1 0 х у у = х2, у
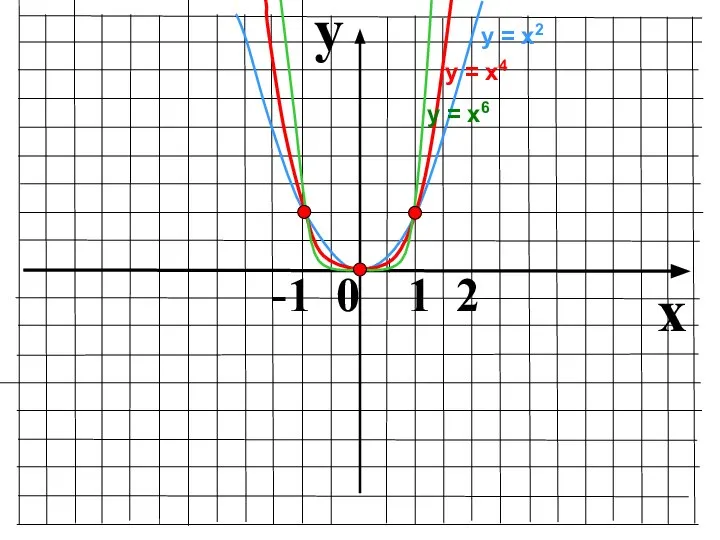
- 7. y x -1 0 1 2 у = х2 у = х6 у = х4
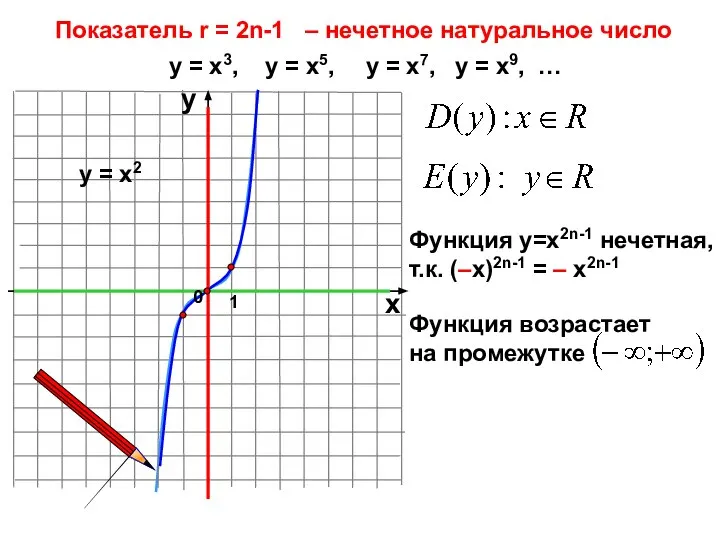
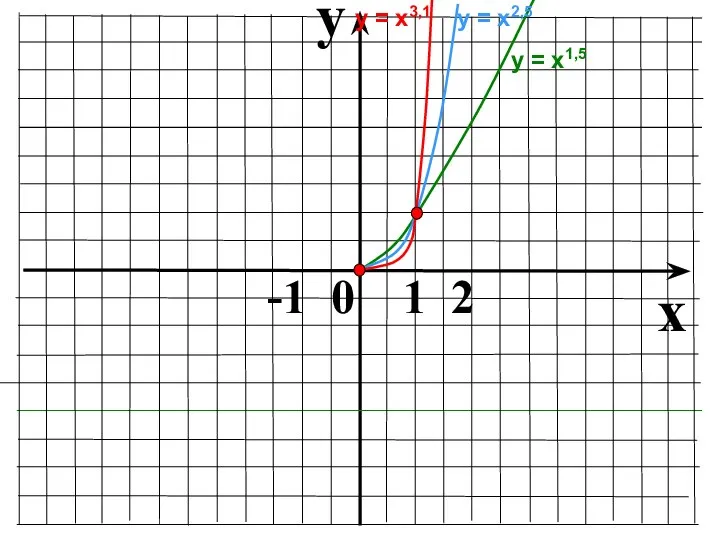
- 8. Показатель r = 2n-1 – нечетное натуральное число 1 х у у = х3, у =
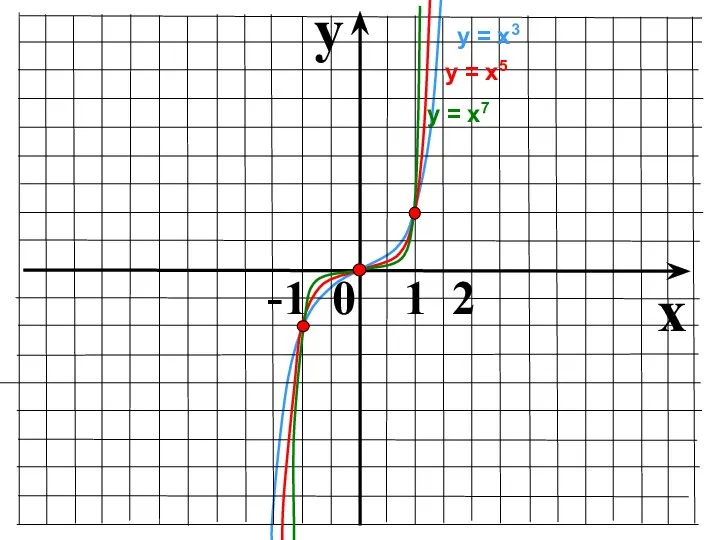
- 9. y x -1 0 1 2 у = х3 у = х7 у = х5
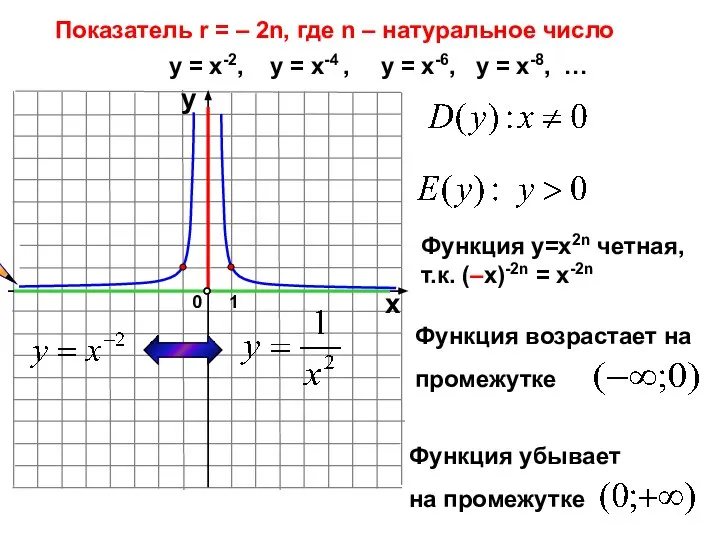
- 10. Показатель r = – 2n, где n – натуральное число 1 0 х у у =
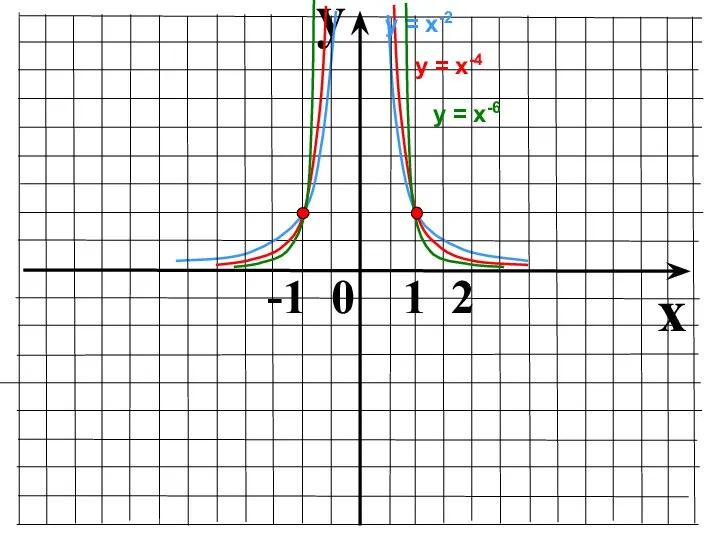
- 11. y x -1 0 1 2 у = х-4 у = х-2 у = х-6
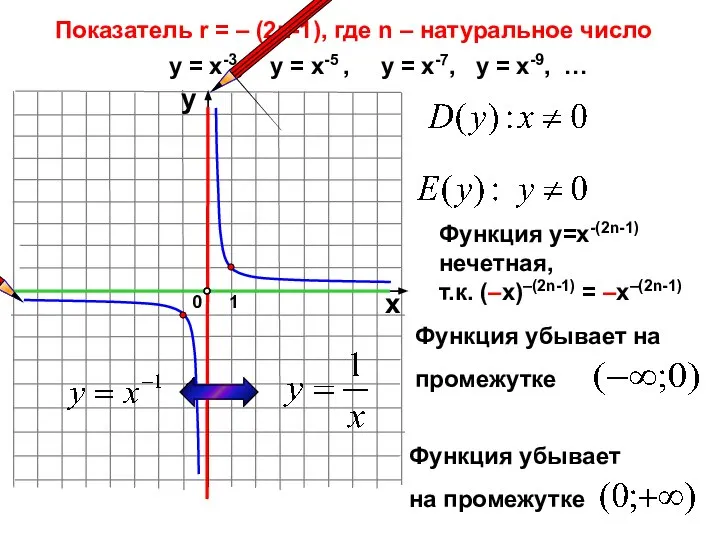
- 12. Показатель r = – (2n-1), где n – натуральное число 1 0 х у у =
- 13. y x -1 0 1 2 у = х-1 у = х-3 у = х-5
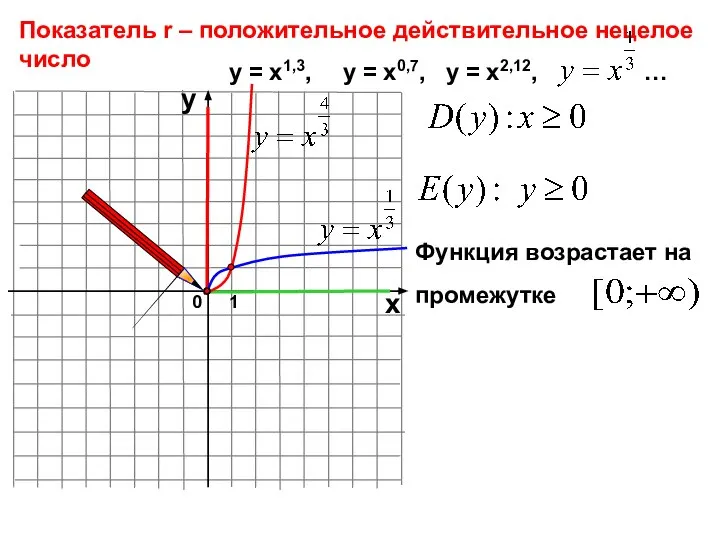
- 14. 0 Показатель r – положительное действительное нецелое число 1 х у у = х1,3, у =
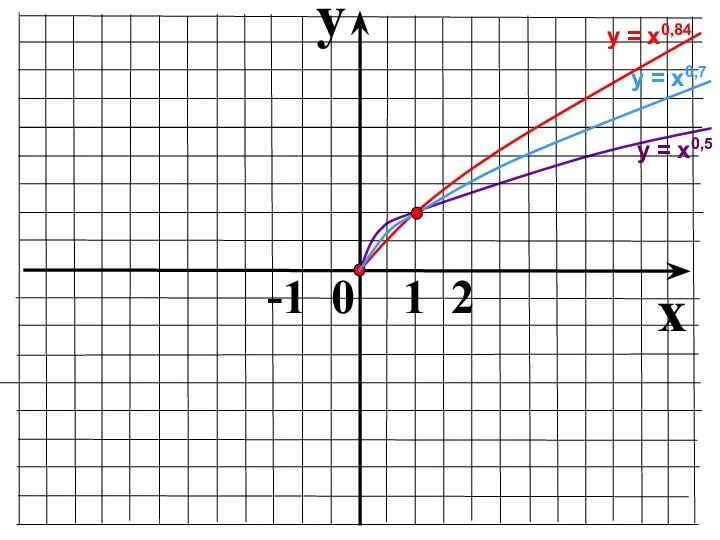
- 15. y x -1 0 1 2 у = х0,5
- 16. y x -1 0 1 2
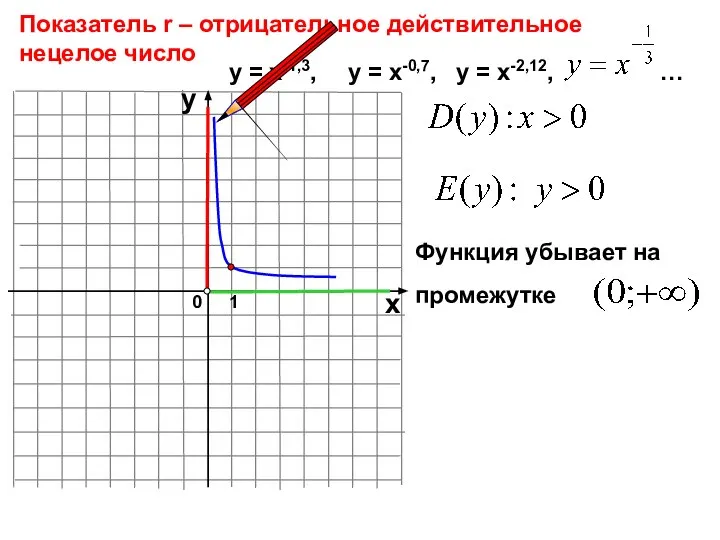
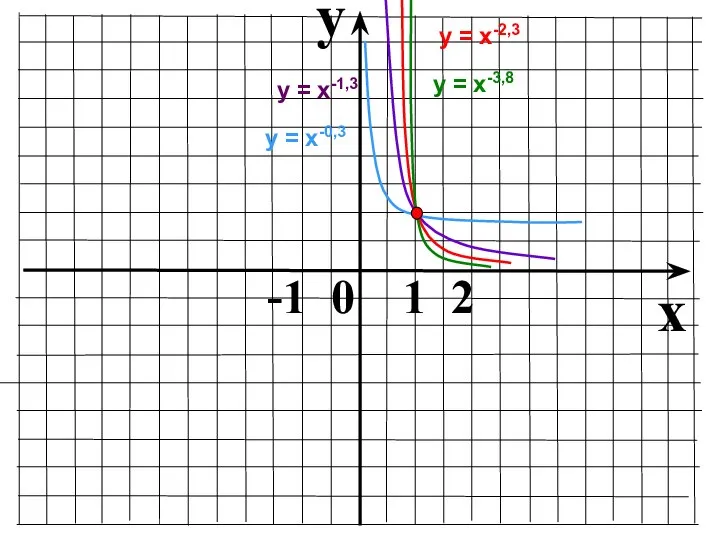
- 17. 0 Показатель r – отрицательное действительное нецелое число 1 х у у = х-1,3, у =
- 18. y x -1 0 1 2
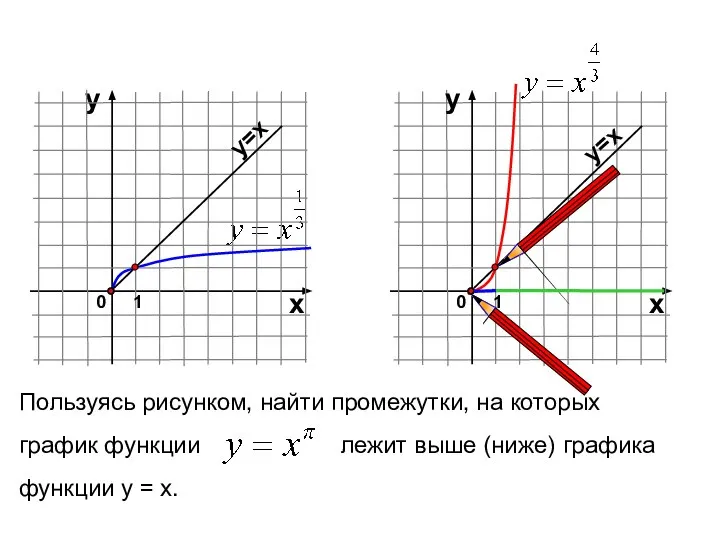
- 19. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
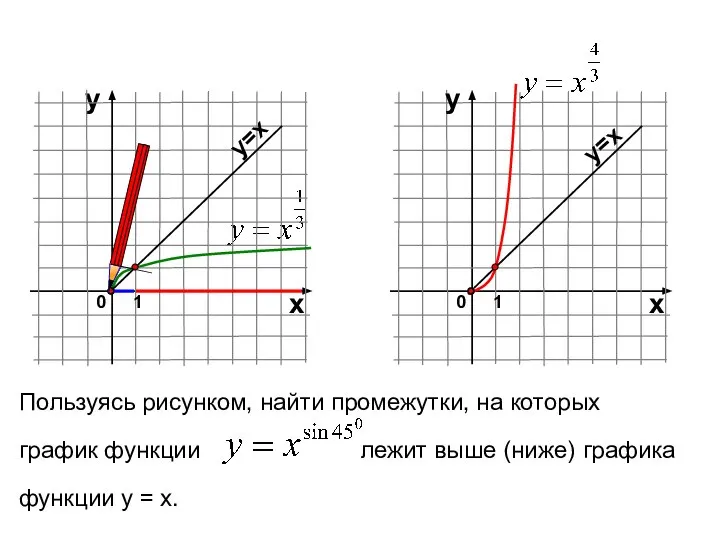
- 20. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
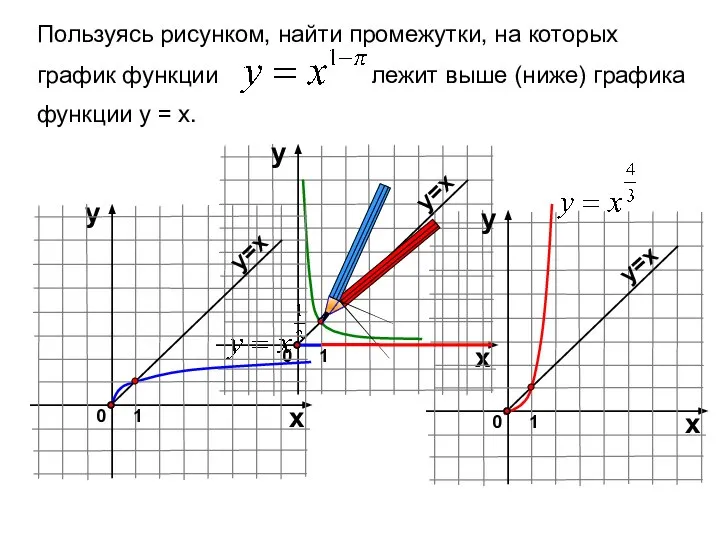
- 21. Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.
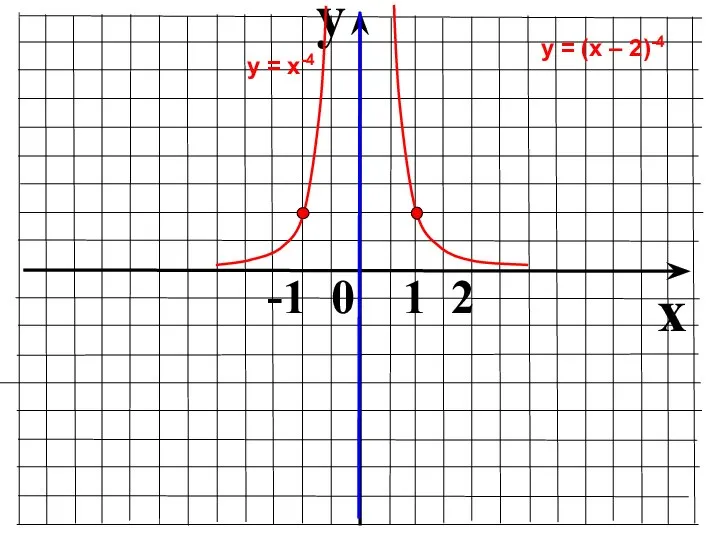
- 22. y x -1 0 1 2 у = х-4 у = (х – 2)-4
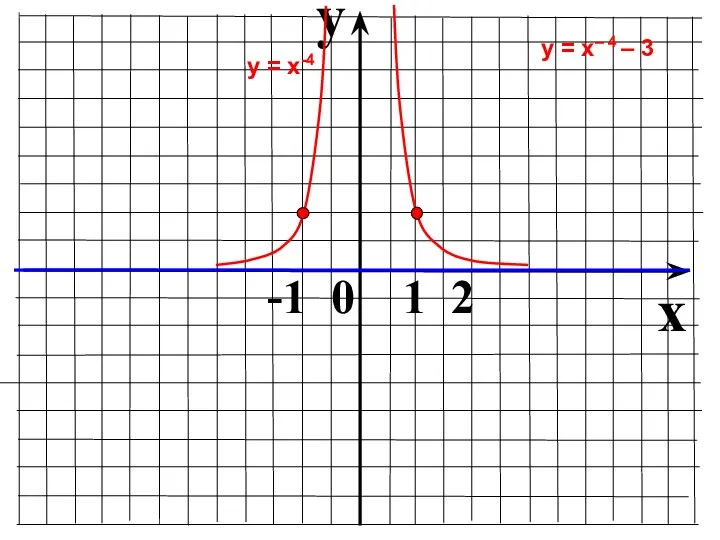
- 23. y x -1 0 1 2 у = х-4 у = х– 4 – 3
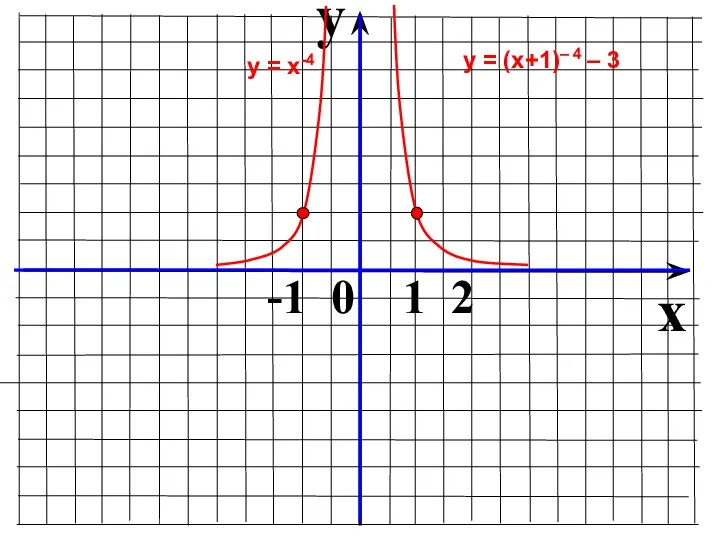
- 24. y x -1 0 1 2 у = х-4 у = (х+1)– 4 – 3
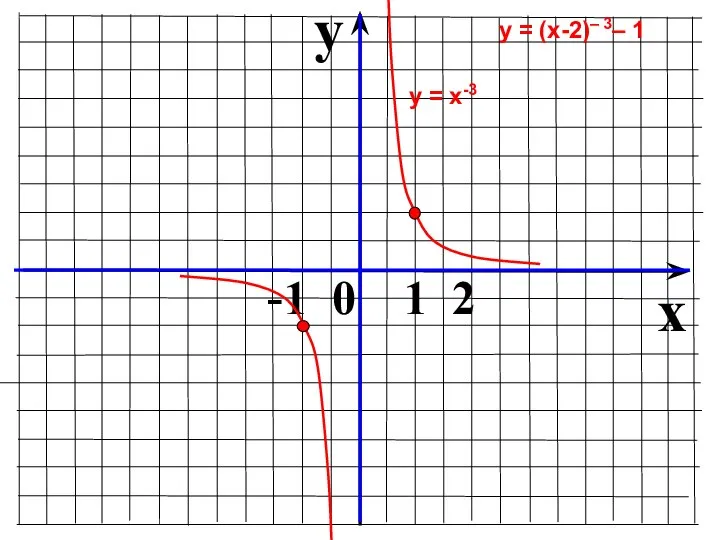
- 25. y x -1 0 1 2 у = х-3 у = (х-2)– 3– 1
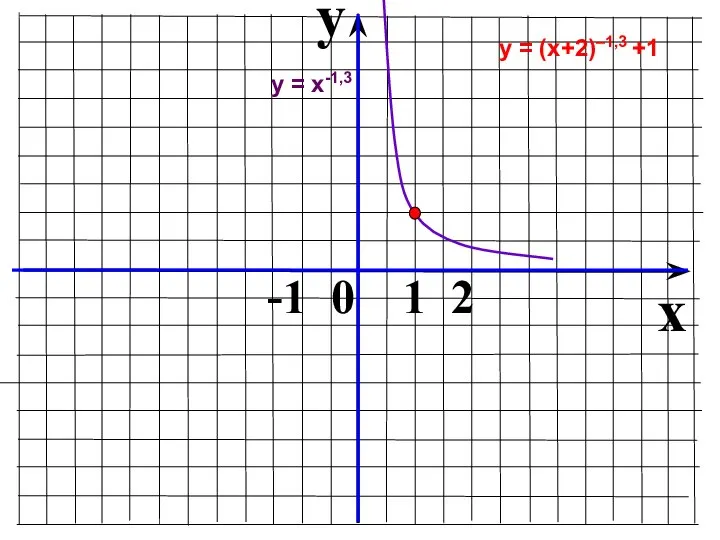
- 26. y x -1 0 1 2 у = (х+2)–1,3 +1 у = х-1,3
- 28. Скачать презентацию




 Угол между векторами
Угол между векторами Использование алгебры логики. Задача про карабли
Использование алгебры логики. Задача про карабли Решение задач по стереометрии
Решение задач по стереометрии Случайные величины. Тема 3. Часть
Случайные величины. Тема 3. Часть Параллелограмм
Параллелограмм Вычисление определенных интегралов
Вычисление определенных интегралов Единица измерения объёма жидкости-литр
Единица измерения объёма жидкости-литр Закрепление решения задач на приведение к единице
Закрепление решения задач на приведение к единице Свойства функций
Свойства функций Свойства ранга матрицы
Свойства ранга матрицы Сложение и вычитание чисел
Сложение и вычитание чисел Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Спин и расширенное супервремя. Суперсимметрия и суперпространство
Спин и расширенное супервремя. Суперсимметрия и суперпространство Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов
Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов Задачи на нахождение четвёртого пропорционального
Задачи на нахождение четвёртого пропорционального Свойства функции
Свойства функции Презентация на тему Степень числа. Квадрат и куб числа
Презентация на тему Степень числа. Квадрат и куб числа  Векторная алгебра
Векторная алгебра Օբյեկտ-կողմնորոշված ծրագրավորման լեզու
Օբյեկտ-կողմնորոշված ծրագրավորման լեզու Четные и нечетные функции
Четные и нечетные функции Подобные треугольники. Признаки подобия треугольников
Подобные треугольники. Признаки подобия треугольников Степень числа а с натуральным показателем
Степень числа а с натуральным показателем Преобразование графиков функций
Преобразование графиков функций Интегративные процессы математического образования и профессиональная подготовка учащихся
Интегративные процессы математического образования и профессиональная подготовка учащихся Урок 9 (29.09.22) Решение задач
Урок 9 (29.09.22) Решение задач Число π. Длина окружности
Число π. Длина окружности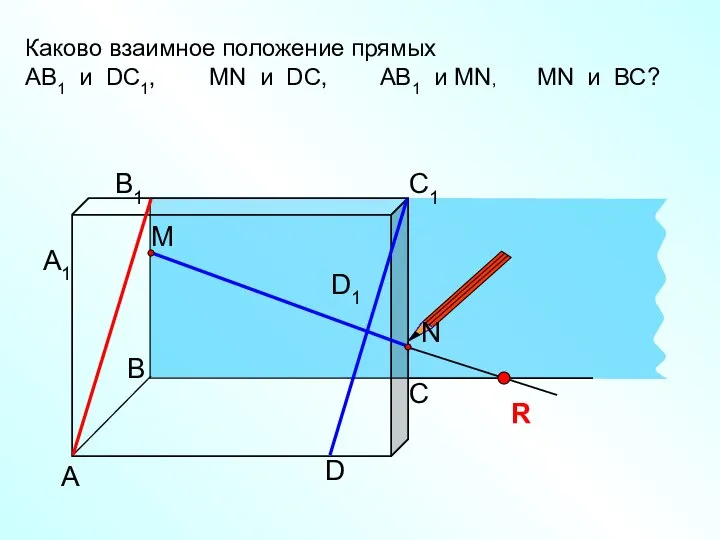 параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10 Составление текстовых задач по математике , связанные с историей, литературой, географией и др
Составление текстовых задач по математике , связанные с историей, литературой, географией и др