Содержание
- 2. Тема урока: Сдвиг графика функции у = ах² вдоль осей координат.
- 3. Перед человеком к разуму три пути: путь размышления – это самый благородный путь, путь подражания –
- 4. Проверьте себя! Задание №1. Ответ: Парабола, Ось у, Вверх, Вниз. Задание №2. Ответ: 1, 2, 5.
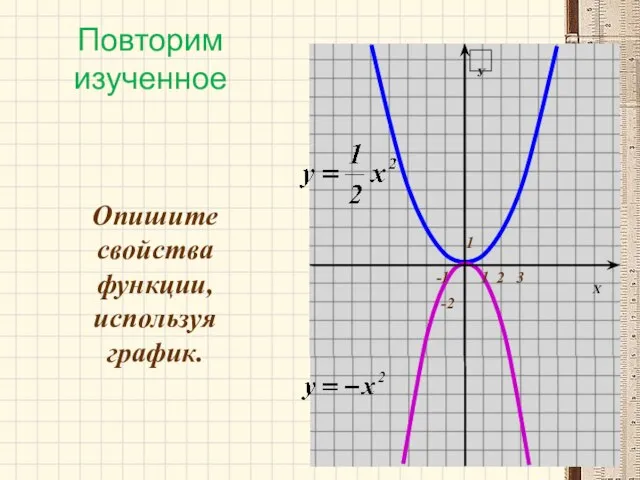
- 5. Повторим изученное У Х 3 2 1 -1 -2 1 Опишите свойства функции, используя график.
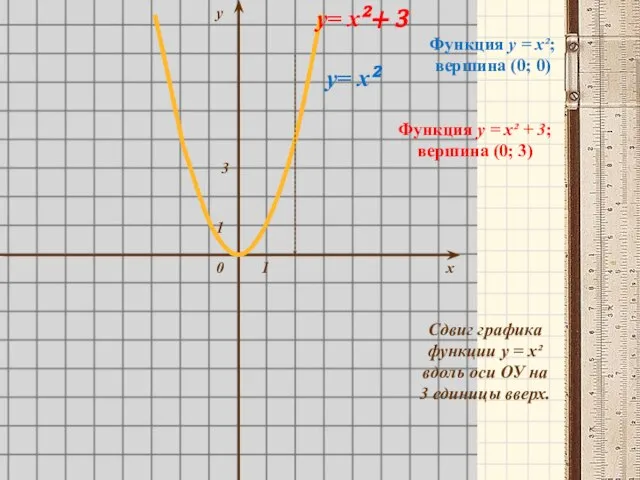
- 6. у х 0 1 1 3 у= х² у= х²+ 3 Функция у = х²; вершина
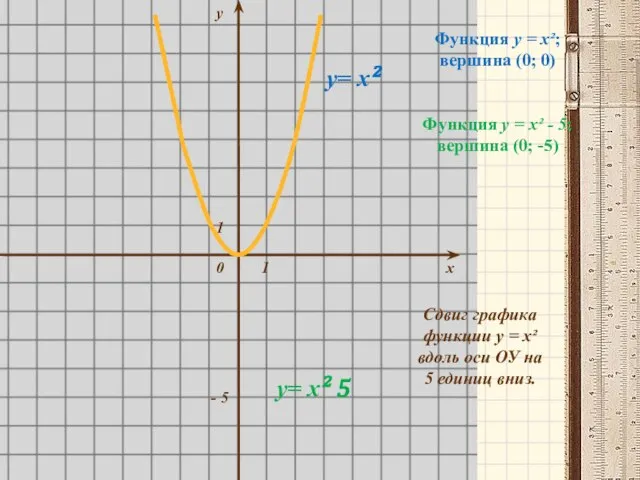
- 7. у 1 1 0 х - 5 у= х² у= х² 5 Функция у = х²;
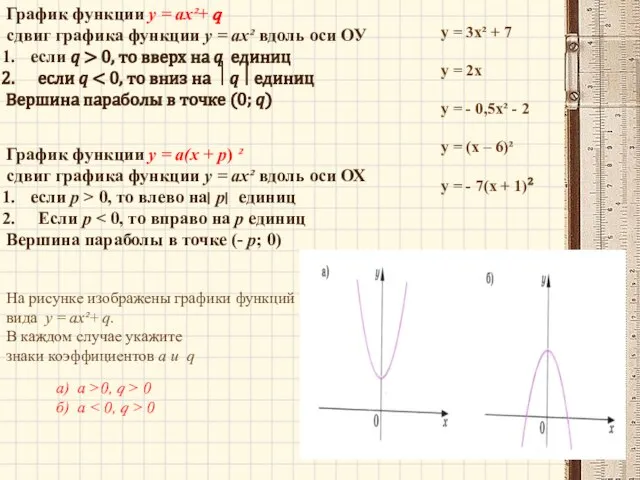
- 8. График функции у = ах² + ? сдвиг графика функции у = ах² вдоль оси ОУ
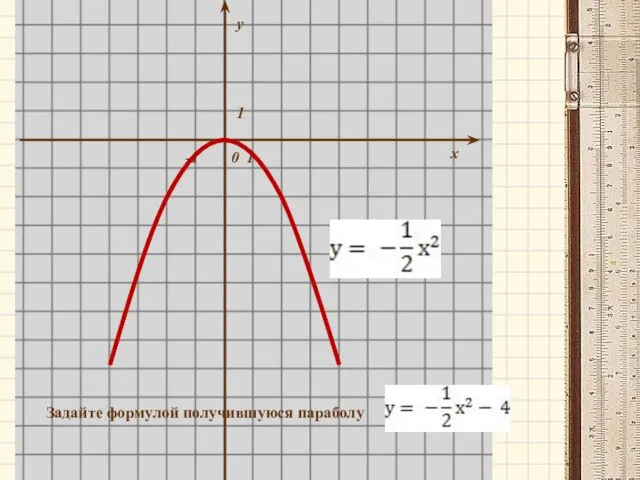
- 9. у Задайте формулой получившуюся параболу х 1 1 -1 0
- 10. 1. Что представляет собой функция у = а( х2 + р)? 2. Составьте алгоритм получения графика
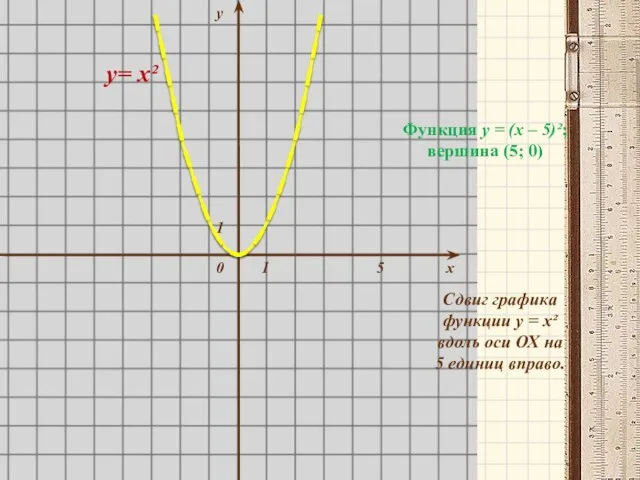
- 11. у 1 1 0 х 5 у= х² Функция у = (х – 5)²; вершина (5;
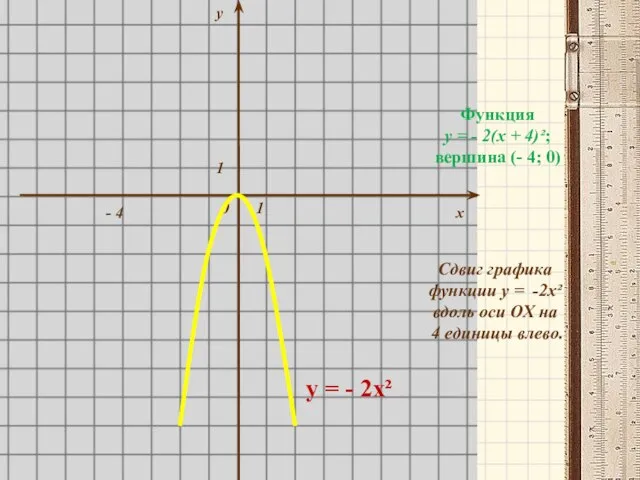
- 12. у 1 0 1 х у = - 2х² - 4 Функция у = - 2(х
- 13. Отдохнём!
- 14. График функции у = ах²+ ? сдвиг графика функции у = ах² вдоль оси ОУ если
- 15. Воспроизведите по памяти алгоритм получения графика функции у = ах² + ? М О Л О
- 16. Контрольный тест. Вариант 1. Уровень 1. а) б) а) в) Уровень 2. Х р > 0
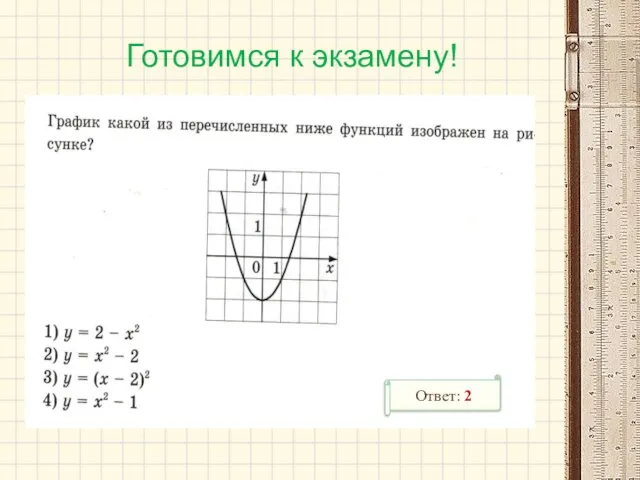
- 17. Готовимся к экзамену! Ответ: 2
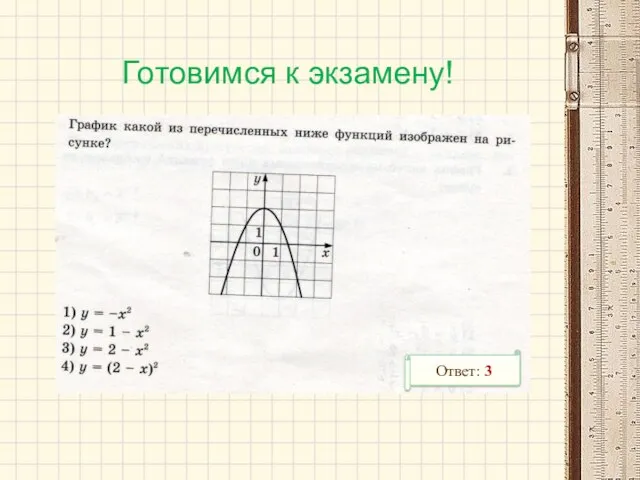
- 18. Ответ: 3 Готовимся к экзамену!
- 19. Оцени свою работу
- 20. 1 УРОВЕНЬ: №212(Б), №222 (Б) 2. УРОВЕНЬ: №218 (Б), № 228 (А) ДЛЯ ВЫПОЛНЕНИЯ № 228
- 21. Правила написания синквейна: -первая строка – одно слово (существительное); -вторая строка – два слова (прилагательные); -третья
- 22. «Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше». Эмиль Золя Эмиль
- 24. Скачать презентацию












 Параллельные прямые
Параллельные прямые Угол между векторами
Угол между векторами Поле чудес. Геометрия
Поле чудес. Геометрия Единица массы - килограмм
Единица массы - килограмм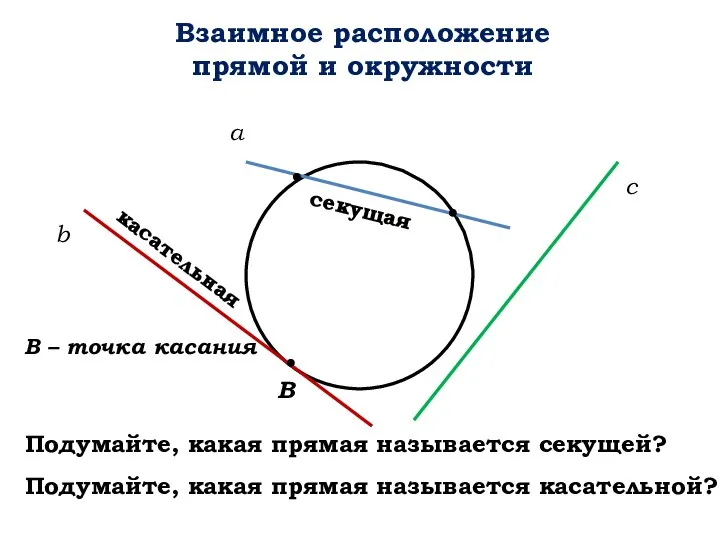 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Действия с десятичными дробями 5 класс
Действия с десятичными дробями 5 класс Старинные системы мер
Старинные системы мер Лекция 8
Лекция 8 Линейная алгебра. Определители
Линейная алгебра. Определители Исследование функций и построение графиков
Исследование функций и построение графиков Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число 08.09
08.09 Графовые модели. Основные понятия. Принцип планирования многошаговых процессов
Графовые модели. Основные понятия. Принцип планирования многошаговых процессов Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента
Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Осевая симметрия
Осевая симметрия Задачи
Задачи Aproximarea numerică a funcţiilor. Metode numerice – curs 10
Aproximarea numerică a funcţiilor. Metode numerice – curs 10 Случайные величины. Таблицы распределения
Случайные величины. Таблицы распределения Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Арифметический квадратный корень
Арифметический квадратный корень Степень многочлена
Степень многочлена Презентация на тему Методы решения квадратных уравнений
Презентация на тему Методы решения квадратных уравнений  Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Начертательная геометрия
Начертательная геометрия Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников Определение координаты движущегося тела
Определение координаты движущегося тела Умножение и деление комплексных чисел
Умножение и деление комплексных чисел