Содержание
- 2. Что знаем? Определение многочлена Многочлен – это сумма одночленов Подобные члены многочлена Это одночлены, имеющие одинаковую
- 3. Что умеем? Приводить многочлен к стандартному виду Находить значение многочлена Определять степень многочлена Выполнять сложение и
- 4. Распределительный закон умножения Чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и
- 5. Раскройте скобки: 3(2х-5) = 6х-15 (5а-1) 4 = 20а- 4 - 1 2 (4 +2у) =
- 6. Одночленом называют сумму числовых и буквенных множителей. Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом
- 7. Чему хотим научиться? 1.Изучить правило умножения многочлена на одночлен 2. Научиться применять его при преобразовании выражений
- 8. Умножение одночлена на многочлен «Корень учения горек, зато плод его сладок» Тема урока:
- 9. 3(2х-5) = =3*2х-3*5= =6х-15 Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член
- 10. ПРИМЕР 1: Умножим одночлен -3xy на многочлен 2x2y+4xy2-1 -3xy∙(2x2y+4xy2-1) = =-3xy∙2x2y+(-3xy)∙4xy2+(-3xy)∙(-1)= =-6x3y2-12x2y3+3xy
- 11. ПРИМЕР 2: Упростим выражение: 4a(2a+5)+2a(3a-1)-1,5a(2a-4) 4a(2a+5)+2a(3a-1)-1,5a(2a-4)= =8a2+20a+6a2-2a-3a2+6a= =11a2+24a
- 12. Выполните упражнения №356, 360 Стр 71
- 14. Скачать презентацию











 Логические задачи. Математика и информатика. Тетрадь для 1–2 классов
Логические задачи. Математика и информатика. Тетрадь для 1–2 классов Л.10_Непрерывность функции
Л.10_Непрерывность функции График функции у = ах 2 + bх + qс
График функции у = ах 2 + bх + qс Презентация на тему Цифра 3
Презентация на тему Цифра 3  Противоположные числа. 6 класс
Противоположные числа. 6 класс Решение задач на проценты
Решение задач на проценты Решение задач
Решение задач Математические ребусы
Математические ребусы Презентация на тему Логарифмическая функция
Презентация на тему Логарифмическая функция  Отрезки (Начало)
Отрезки (Начало) Действия с натуральными числами. Решение задач, с помощью уравнений
Действия с натуральными числами. Решение задач, с помощью уравнений Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ  Действия над матрицами. Обратная матрица. Лекция 2а
Действия над матрицами. Обратная матрица. Лекция 2а Свойства числовых неравенств. 8 класс
Свойства числовых неравенств. 8 класс Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Алгоритм решения комбинаторных задач
Алгоритм решения комбинаторных задач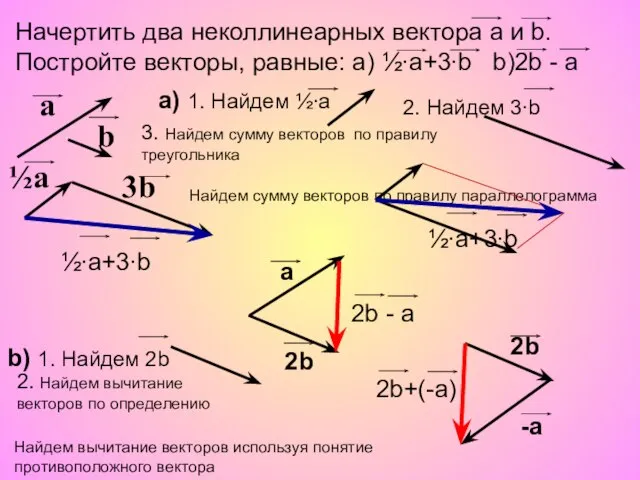 Векторы (9 класс) Задачи
Векторы (9 класс) Задачи Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Спасение похищенных чисел. Урок-сказка
Спасение похищенных чисел. Урок-сказка Путешествие по морям
Путешествие по морям Математический диктант
Математический диктант Презентация на тему Перпендикулярность прямой и плоскости
Презентация на тему Перпендикулярность прямой и плоскости  Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений Блиц-турнир
Блиц-турнир Повторение курса геометрии. 7 класс
Повторение курса геометрии. 7 класс Математика. Билет 5
Математика. Билет 5 Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Подготовка к ЕГЭ. Повторение. Математика
Подготовка к ЕГЭ. Повторение. Математика