Взаимное расположение прямой и окружности

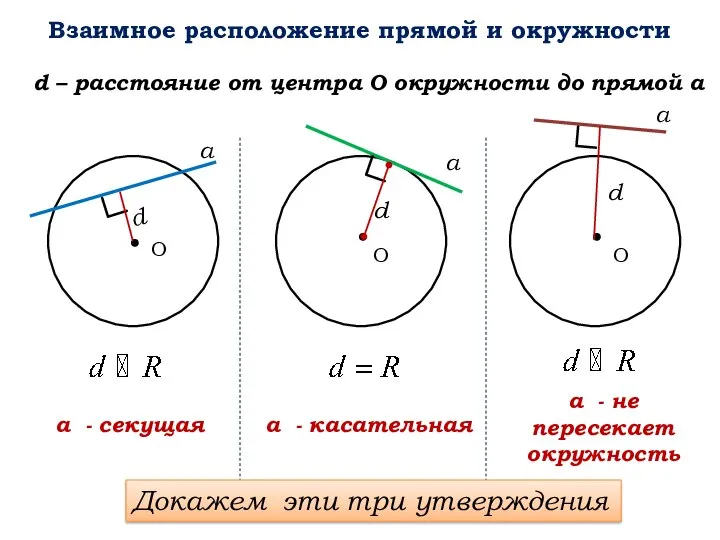
Взаимное расположение прямой и окружности
О
О
О
d – расстояние от центра О окружности до прямой а
а
а
а
d
d
d
а - секущая
а - касательная
а - не пересекает окружность
Докажем эти три утверждения

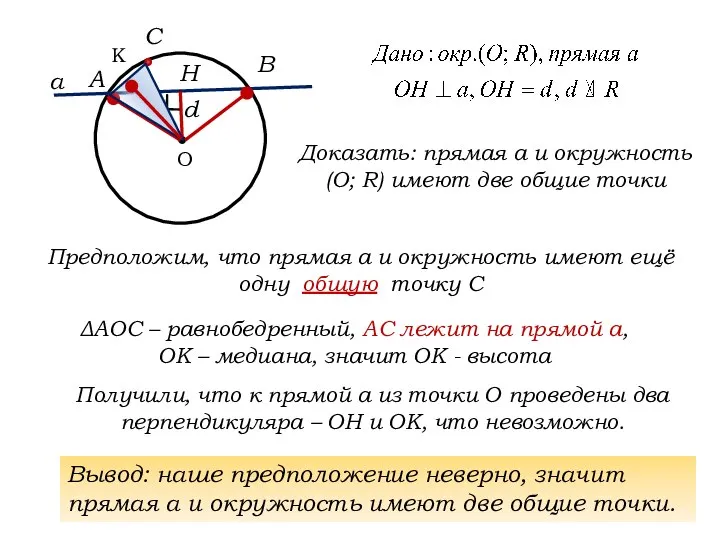
О
Доказать: прямая а и окружность (О; R) имеют две общие точки
а
d
Н
А
А
В
Вывод: Точки A и В лежат на окружности, то есть прямая и окружность имеют две общие точки
1 случай
Отложим на прямой а от точки Н два отрезка НВ и НА:
Проведем отрезки ОА и ОВ

О
Доказать: прямая а и окружность (О; R) имеют две общие точки
а
d
Н
Предположим, что прямая а и окружность имеют ещё одну общую точку С
А
А
В
С
К
Вывод: наше предположение неверно, значит прямая а и окружность имеют две общие точки.
Получили, что к прямой а из точки О проведены два перпендикуляра – ОН и ОК, что невозможно.
ΔАОС – равнобедренный, АС лежит на прямой а,
ОК – медиана, значит ОК - высота

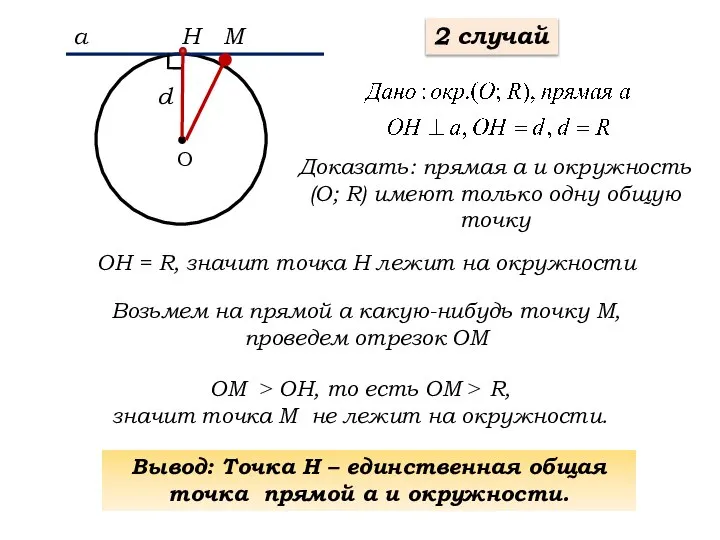
О
Доказать: прямая а и окружность (О; R) имеют только одну общую точку
а
d
Н
ОН = R, значит точка Н лежит на окружности
А
М
Вывод: Точка Н – единственная общая точка прямой а и окружности.
Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ
ОМ > ОН, то есть ОМ > R,
значит точка М не лежит на окружности.
2 случай

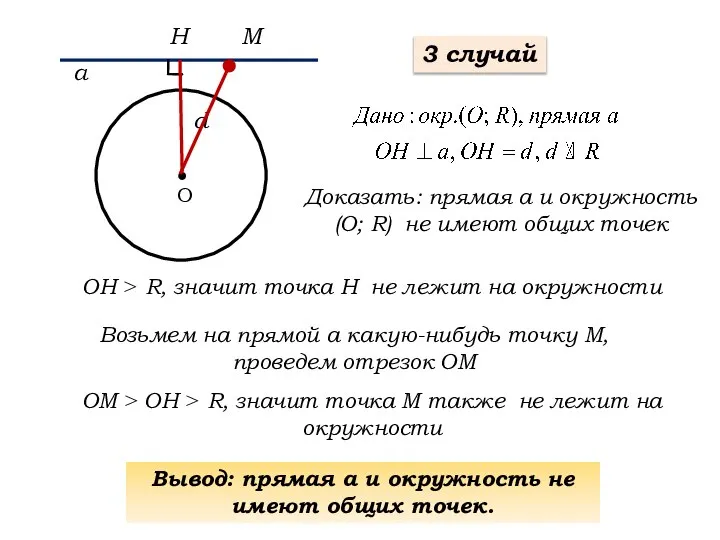
О
Доказать: прямая а и окружность (О; R) не имеют общих точек
а
d
Н
ОН > R, значит точка Н не лежит на окружности
А
Вывод: прямая а и окружность не имеют общих точек.
Возьмем на прямой а какую-нибудь точку М, проведем отрезок ОМ
М
ОМ > ОН > R, значит точка М также не лежит на окружности
3 случай

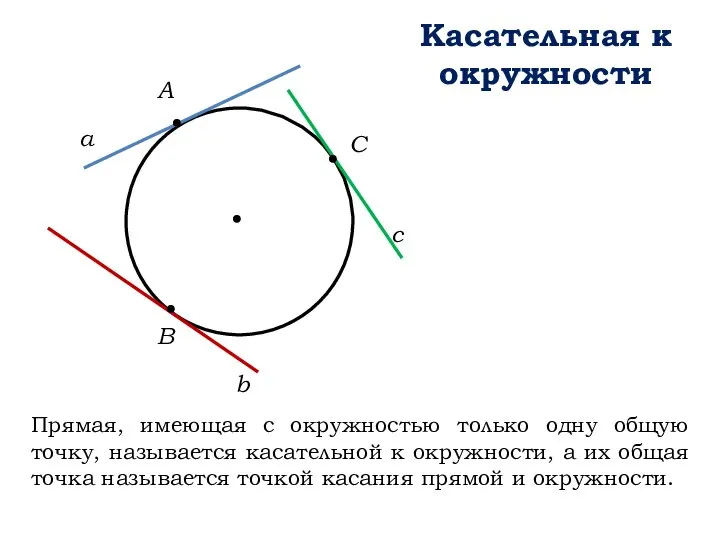
Касательная к окружности
а
b
c
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
В
А
С

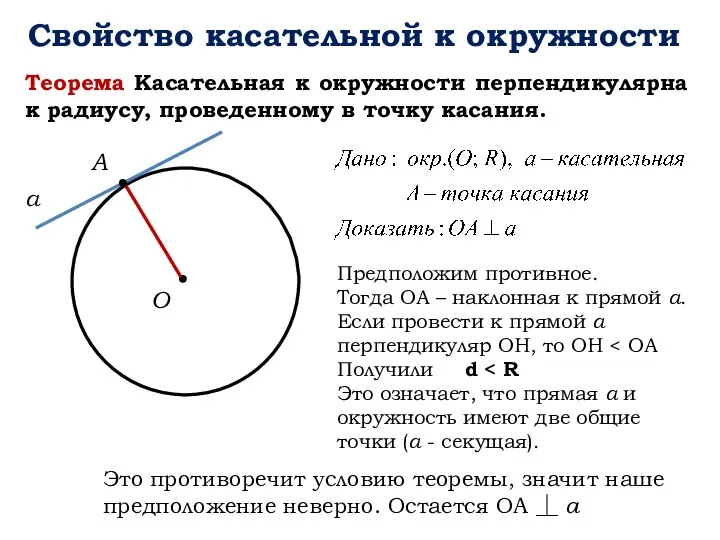
Свойство касательной к окружности
а
Теорема Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
А
О
Предположим противное.
Тогда ОА – наклонная к прямой а.
Если провести к прямой а перпендикуляр ОН, то ОН < ОА
Получили d < R
Это означает, что прямая а и окружность имеют две общие точки (а - секущая).
Это противоречит условию теоремы, значит наше предположение неверно. Остается ОА ⏊ а

Признак касательной к окружности
а
Обратная теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикуляр-на к этому радиусу, то она является касательной
А
О
d
d = R,
значит прямая а и окружность имеют одну общую точку.
Вывод: а - касательная

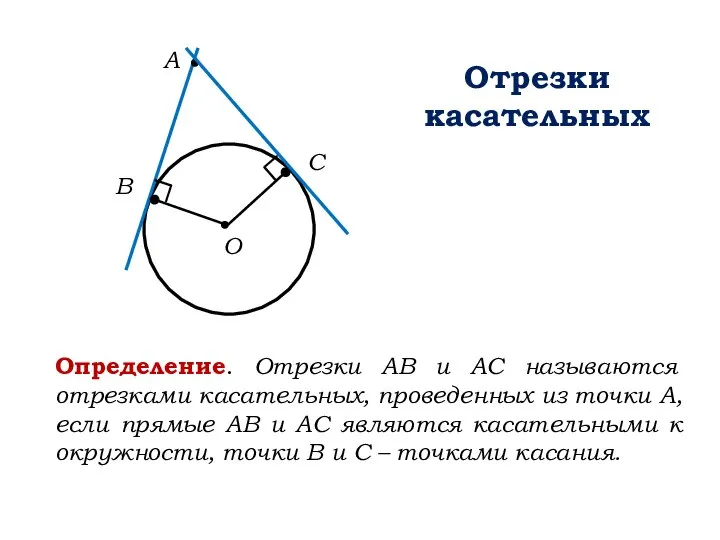
Отрезки касательных
B
А
О
C
Определение. Отрезки АВ и АС называются отрезками касательных, проведенных из точки А, если прямые АВ и АС являются касательными к окружности, точки В и С – точками касания.

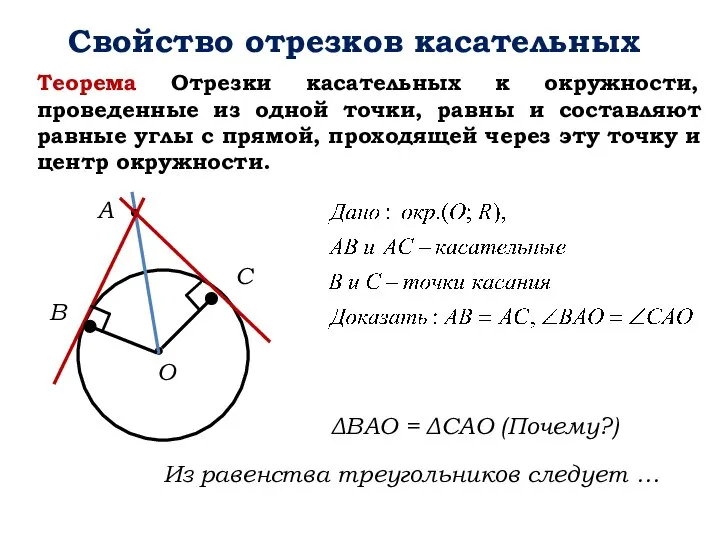
Свойство отрезков касательных
B
Теорема Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
А
О
C
ΔBAO = ΔCAO (Почему?)
Из равенства треугольников следует …

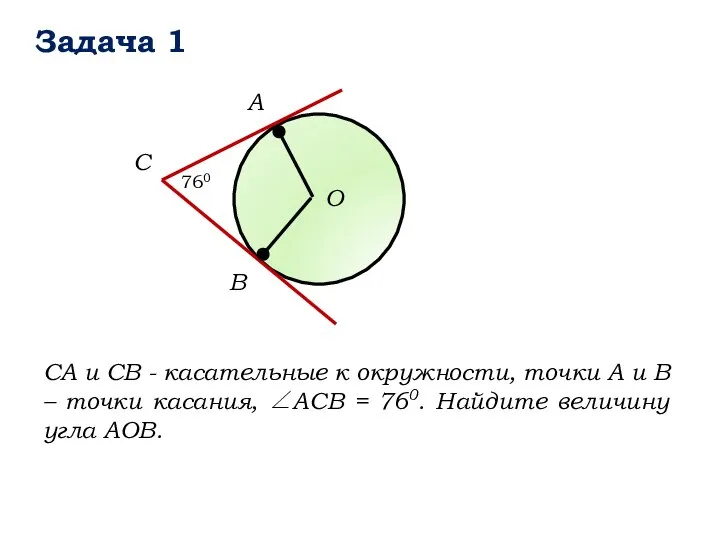
Задача 1
B
А
О
C
СА и СВ - касательные к окружности, точки А и В – точки касания, ∠АСВ = 760. Найдите величину угла АОВ.
760

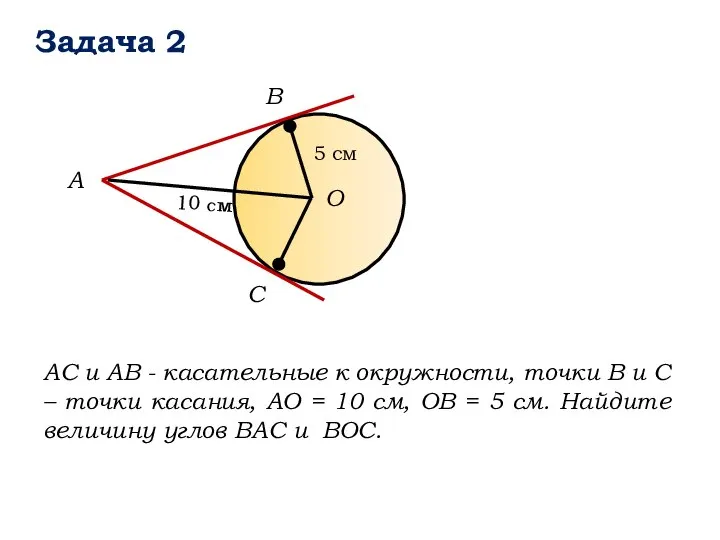
Задача 2
B
А
О
C
АС и АВ - касательные к окружности, точки В и С – точки касания, АО = 10 см, ОВ = 5 см. Найдите величину углов ВАС и ВОС.
10 см
5 см

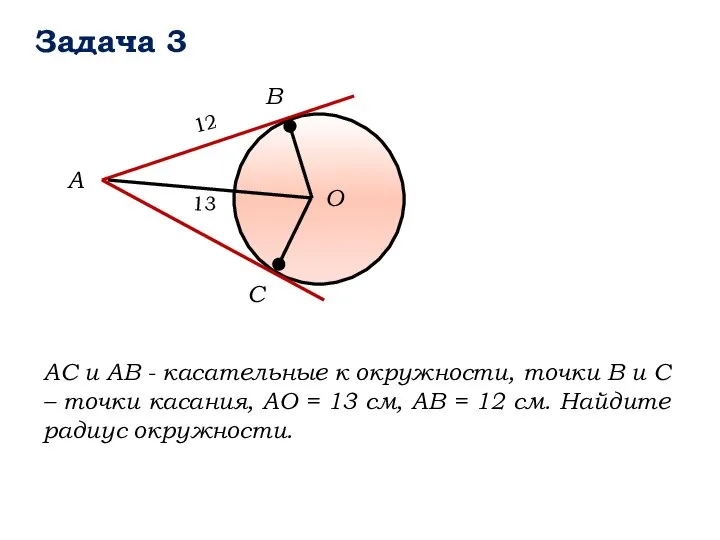
Задача 3
B
А
О
C
АС и АВ - касательные к окружности, точки В и С – точки касания, АО = 13 см, АВ = 12 см. Найдите радиус окружности.
13
12