Аналитическое (письменное) счисление координат

Основные формулы аналитического счисления
Судно из точки А (φ1 λ1), следуя постоянным курсом (К) по локсодромии, пришло в точку В (φ2 λ2).
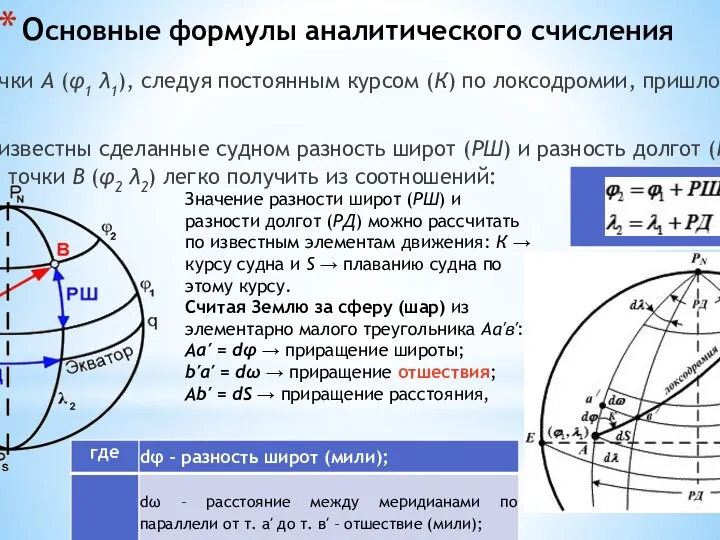
Если будут известны сделанные судном разность широт (РШ) и разность долгот (РД) то координаты точки В (φ2 λ2) легко получить из соотношений:
Значение разности широт (РШ) и разности долгот (РД) можно рассчитать по известным элементам движения: К → курсу судна и S → плаванию судна по этому курсу.
Считая Землю за сферу (шар) из элементарно малого треугольника Аа′в′:
Aa′ = dφ → приращение широты;
b′a′ = dω → приращение отшествия;
Ab′ = dS → приращение расстояния,

Продолжение
Если Δ Аа′в′ принять за плоский, можно написать дифференциальные уравнения:
В результате интегрирования значений dφ и dω при K = const, получим:
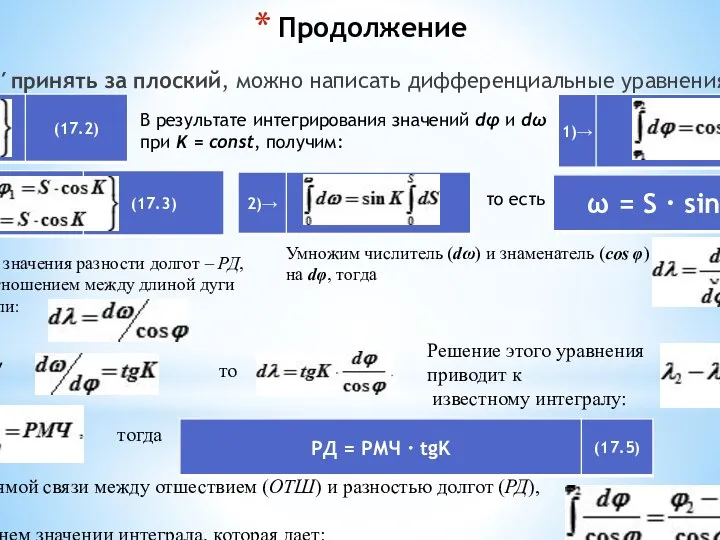
то есть
то есть
Для вычисления значения разности долгот – РД, воспользуемся соотношением между длиной дуги экватора и параллели:
Умножим числитель (dω) и знаменатель (cos φ)
на dφ, тогда
так как из Δ Аа′в′
то
Решение этого уравнения
приводит к
известному интегралу:
а
тогда
Для вывода прямой связи между отшествием (ОТШ) и разностью долгот (РД),
используем
теорему о среднем значении интеграла, которая дает:

Продолжение
где φn – промежуточное значение широты в интервале между φ1 и φ2.
Тогда для разности долгот – РД можно написать:
Приравняв оба значения
разности долгот (РД),
полученного
по формулам (17.5) и (17.6),
получим значение
промежуточной широты φn:
откуда
Подставив значение соs φn (формула 17.8) в формулу (17.6)
для разности долгот (РД) и учтя, что
окончательно получим:
где отшествие (ОТШ) и разность широт (РШ) в милях.
Таким образом отшествие (ОТШ) представляет собой длину параллели (в милях)
между меридианами точек А и В, широта которой (параллели) определяется соотношением

Продолжение
На практике, при ведении аналитического учета на коротких расстояниях,
можно допустить, что в интервале от φ1 до φ2 значение cos φ изменяется линейно, тогда
и приближенная формула для расчета
разности долгот – РД примет вид:
то есть разность долгот (РД) равна отшествию (ОТШ), деленному на косинус средней широты (φm).
По формулам (17.3) и (17.4) составлены таблица 24 «МТ-75» (с. 260÷272) и таблица 2.19а «МТ-2000» (с. 282÷294) «Разность широт и отшествие». В этих таблицах по плаванию S (от 0 до 100 миль) и курсу (через 1°) можно получить готовые значения разности широт (РШ) и отшествия (ОТШ), величины которых даны в таблице до сотых долей мили и поэтому могут быть использованы для плаваний (S) в 10 и 100 раз больших (или меньших) → переносом запятой → см. табл. 17.8.

Практические расчёты
В «МТ-75» помещена также специальная таблица 25а «Разность долгот» (с. 273÷278)
составленная по формуле (17.13).
Аналогичная таблица 2.20 – см. «МТ-2000» (с. 296÷301).
Разность широт и отшествие
(с. 271 «МТ-75» или с. 293 «МТ-2000»)
Получение значений разности долгот (РД) для десятков или сотен миль значений отшествия (ОТШ) делается простым переносом запятой, отделяющей целую часть от дробной в найденных табличных значениях.

Практические расчёты
Решение:
ОТШ = 246′ = 100 + 100 + 40 + 6.
По значениям 100, 100, 40 и 6 для φCP = 40° из табл. 25а «МТ-75» (с. 273) или табл. 2.20 «МТ-2000» (с. 296) выбираем значения разности долгот (см. табл. 17.2):
Таблица 17.2.
Ответ: РД = 321,0′ к W.
Решение:
1. → Находим значение φn (см. ф. 17.8).
φ1 = 60°N …. МЧ1 = 4507,4′
φ2 = 20°N…. МЧ2 = 1217,3′
Значения меридиональных частей (МЧ1 и МЧ2) выбираем из табл. 26 «МТ-75» (с. 280÷287) или табл. 2.28а «МТ-2000» (с. 314÷321) → табл. 24.5.