Содержание
- 2. Математика – это просто.
- 3. 26 х 11 = 2 6 (2 + 6 ) = 286 352 = ( 3
- 4. Задачи. В6 . Тригонометрия.
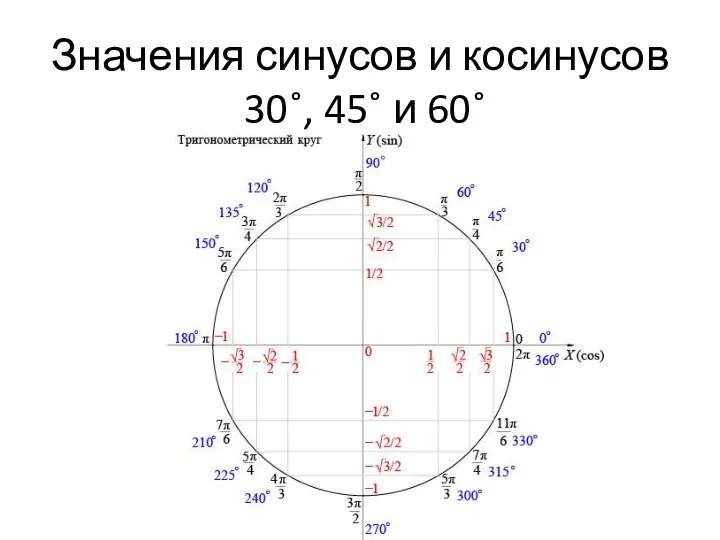
- 5. Значения синусов и косинусов 30˚, 45˚ и 60˚
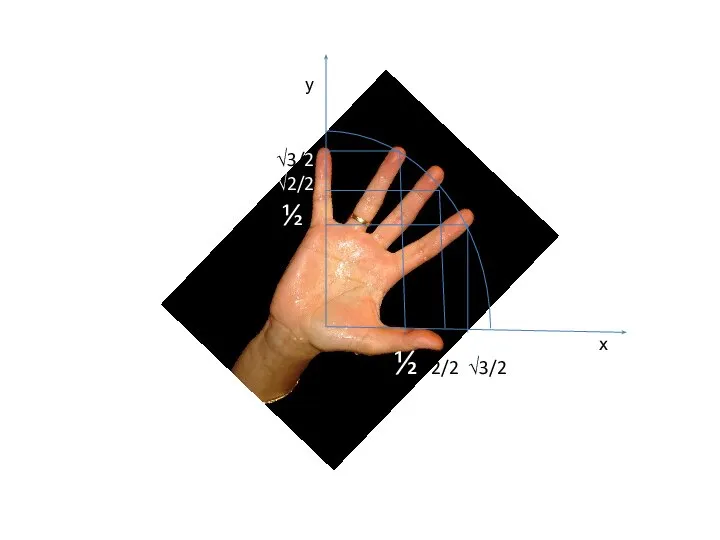
- 6. ½ 2/2 √3/2 √3/2 √2/2 ½ у х
- 7. Стандартное решение задач тригонометрии , - ?
- 8. Т.к. мы знаем, что 5, 12, 13 – пифагорова тройка 13 12 5 - ? ,
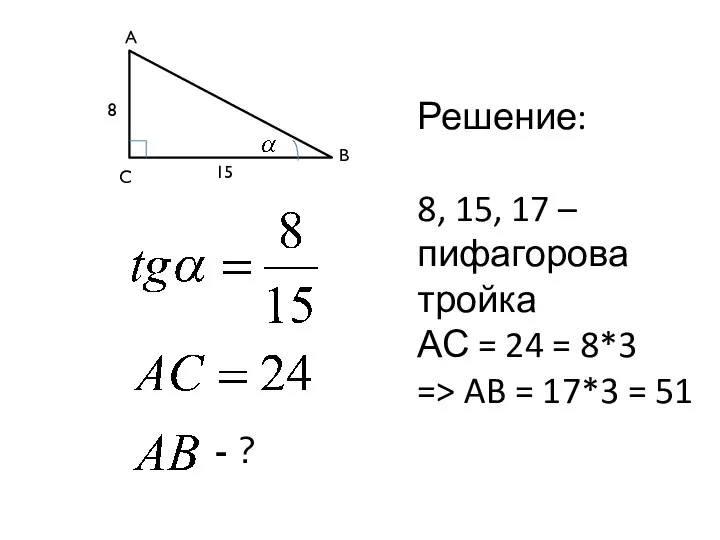
- 9. 8 15 C A B - ? Решение: 8, 15, 17 – пифагорова тройка АС =
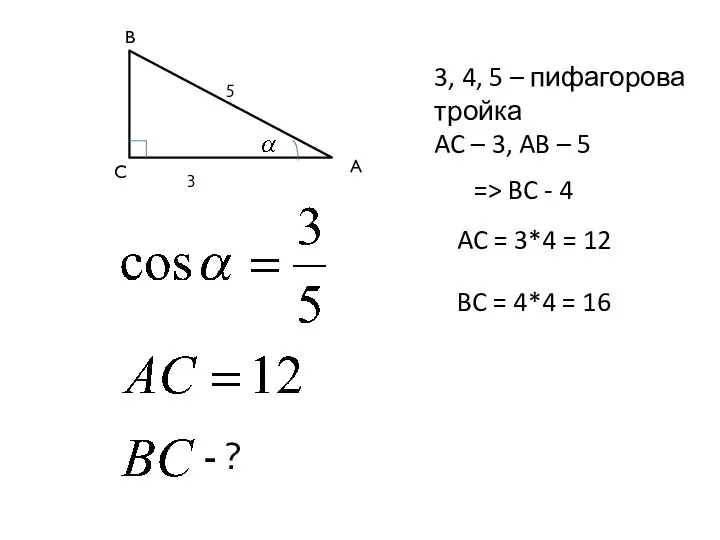
- 10. 5 3 A C B - ? 3, 4, 5 – пифагорова тройка AC – 3,
- 11. В13. задачи на проценты. Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько
- 12. брюки рубашка пиджак 130 100 78 100 100 – 60 = 40 Ответ: 40
- 13. В13. задачи на совместную работу Петя и Витя красят забор за 3 часа, Витя и Игорь
- 14. П + В = 3 часа В + И = 4 часа П + И =
- 15. В14. Найти точки экстремума функции. Найти наибольшее/наименьшее значение функции на отрезке.
- 16. Алгоритм Найти производную Найти критические точки ( у´=0 ) Решить полученное уравнение Отметить на числовой прямой
- 17. Найдите наибольшее значение функции у = 8tgx - 8x + 2π – 6 на отрезке [
- 18. Найдите наименьшее значение функции у = 4х – ln(х + 3)4 на отрезке [ -2,5; 0
- 19. Найдите наименьшее значение функции у = (х – 16)ех-15 на отрезке [ 14; 16]. Ответ: -1
- 21. Скачать презентацию

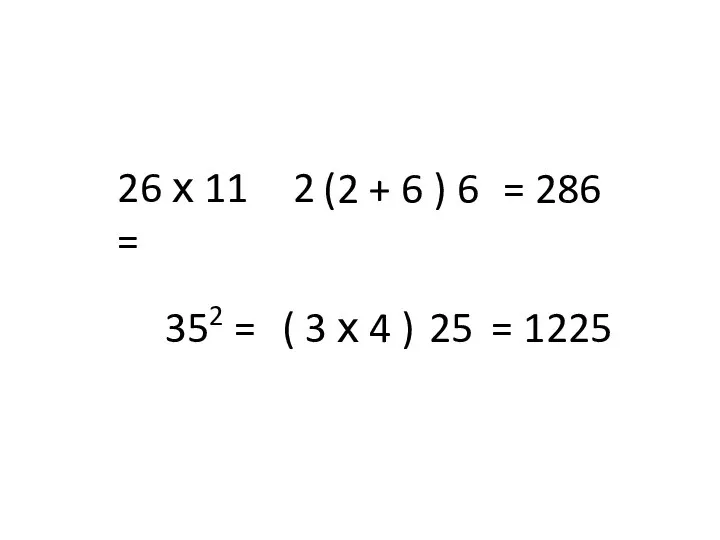


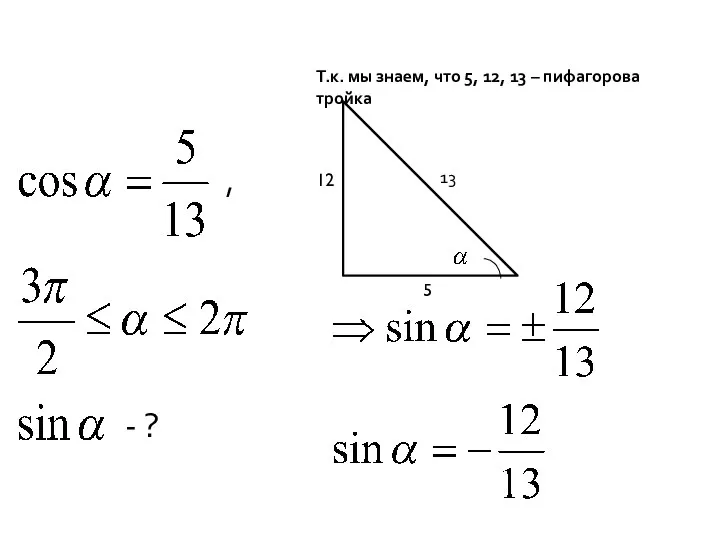








![Найдите наименьшее значение функции у = (х – 16)ех-15 на отрезке [ 14; 16]. Ответ: -1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1010642/slide-18.jpg)
 Смотр знаний: Экскурс по формулам сокращенного умножения
Смотр знаний: Экскурс по формулам сокращенного умножения Подготовка к ЕГЭ. Решение задач
Подготовка к ЕГЭ. Решение задач Своя игра
Своя игра Число и цифра (старшая группа)
Число и цифра (старшая группа) Определение медианы
Определение медианы Решение уравнений
Решение уравнений Обыкновенные дроби
Обыкновенные дроби Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Измерение отрезков
Измерение отрезков Преобразование чисел, полученных при измерении мерами стоимости, длины, массы
Преобразование чисел, полученных при измерении мерами стоимости, длины, массы Сдвиг графика функции у=ах2 вдоль осей координат. Этапы построения графиков функции в Microsoft Excel
Сдвиг графика функции у=ах2 вдоль осей координат. Этапы построения графиков функции в Microsoft Excel Решение планиметрических задач
Решение планиметрических задач Решение задач к главе IV §1,2
Решение задач к главе IV §1,2 Дифференциальное исчисление в нормированных пространствах (задачи)
Дифференциальное исчисление в нормированных пространствах (задачи) Системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной Системы степенных неравенств
Системы степенных неравенств Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Тренажёр. Табличное умножение. В сказочном лесу
Тренажёр. Табличное умножение. В сказочном лесу Трапеция. 8 класс
Трапеция. 8 класс Повторение 1 класс
Повторение 1 класс Международный день головоломки
Международный день головоломки Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Тригонометрические уравнения
Тригонометрические уравнения Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Все ли в мире состоит из многогранников
Все ли в мире состоит из многогранников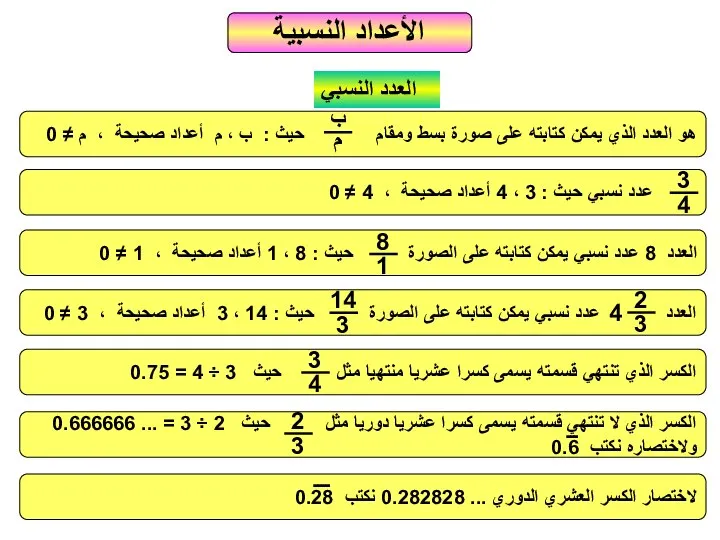 الأعداد انسبية
الأعداد انسبية Логика предикатов. Cостав математической логики
Логика предикатов. Cостав математической логики Поворот и параллельный перенос
Поворот и параллельный перенос