Слайд 2Пример 9.
Решить систему уравнений, используя формулы Крамера:
Решение:
Найдем определитель основной матрицы системы:

Слайд 3, , следовательно, система имеет единственное решение.Найдем его по формулам Крамера:
где

Слайд 4Итак,
Пример 10. Исследовать на совместность и решить систему методом Гаусса:
;

Слайд 5Решение.Найдем ранг расширенной матрицы системы, выполнив элементарные преобразования строк:
~
~
~
~
~

Слайд 6Очевидно, что r(А) = r( )=4, следовательно, система совместна
Очевидно, что r(А) =

r( )=4, следовательно, система совместна, причем имеет единственное решение. Запишем систему, соответствующую последней матрице:
Находим значения неизвестных:
Слайд 7
Находим значения неизвестных:
Итак, решение системы:

Слайд 8Пример 11. Исследовать систему линейных уравнений
и в случае совместности решить ее методом

Гаусса.
Решение
При исследовании системы линейных уравнений используем теорему Кронекера–Капелли: система линейных уравнений совместна, тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Слайд 9Составим расширенную матрицу системы
Чтобы определить ранг матрицы, приведем ее к ступенчатому виду

с помощью элементарных преобразований строк. Матрицы, получаемые после преобразований, являются эквивалентными. Будем обозначать это знаком .
Прибавим сначала ко второй строке первую, умноженную на , а затем к третьей – первую, умноженную на 3:
Слайд 10
Умножим вторую строку матрицы на , третью строку умножим на , получим

матрицу
Прибавим к третьей строке вторую, умноженную на -1 , и получим
Слайд 11Ранг расширенной матрицы равен рангу матрицы системы и равен 2, следовательно, система

имеет решение. Так как ранг матрицы меньше, чем количество переменных в системе, то система имеет бесконечно много решений. Чтобы найти решения, прибавим к первой строке вторую строку, умноженную на -2 :










 Презентация на тему Векторы
Презентация на тему Векторы  Геометрический калейдоскоп
Геометрический калейдоскоп Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Кубический корень
Кубический корень Треугольник и квадранты. Тестирования. Основные понятия
Треугольник и квадранты. Тестирования. Основные понятия Проценты. Устная работа
Проценты. Устная работа Презентация на тему Округление натуральных чисел
Презентация на тему Округление натуральных чисел  SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY Производная функции. Геометрический смысл производной
Производная функции. Геометрический смысл производной Математический турнир Умники и умницы
Математический турнир Умники и умницы Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Способы построения параллельных прямых
Способы построения параллельных прямых Презентация на тему Площадь круга и кругового сектора
Презентация на тему Площадь круга и кругового сектора  Приём вычитания вида 12 -
Приём вычитания вида 12 - Формулы половинного аргумента
Формулы половинного аргумента Гипотеза Коллатца. (доказательство гипотезы)
Гипотеза Коллатца. (доказательство гипотезы) Коэффициент. Упрощение выражений
Коэффициент. Упрощение выражений Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла Powtórzenie do klasówki
Powtórzenie do klasówki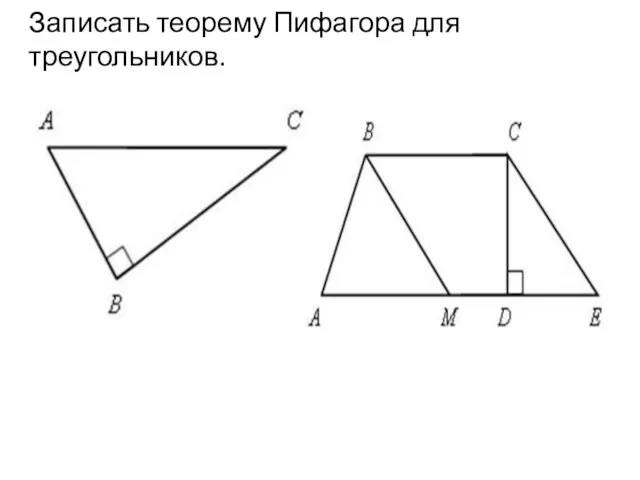 Теорема Пифагора. Урок 24
Теорема Пифагора. Урок 24 Статистические таблицы и графики
Статистические таблицы и графики Логарифмы. Тест по алгебре
Логарифмы. Тест по алгебре Сравнение, сложение и вычитание обыкновенных дробей. 6 класс
Сравнение, сложение и вычитание обыкновенных дробей. 6 класс Письменные приемы вычислений
Письменные приемы вычислений Спектральное представление ССП
Спектральное представление ССП Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам
Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам Булева алгебра. Классы булевых функций. Шаблон решения контрольной работы
Булева алгебра. Классы булевых функций. Шаблон решения контрольной работы Презентация по математике "Использование информационных технологий в преподавании математики" -
Презентация по математике "Использование информационных технологий в преподавании математики" -