Содержание
- 2. Определение производной Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим
- 3. Определение производной Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке интервала
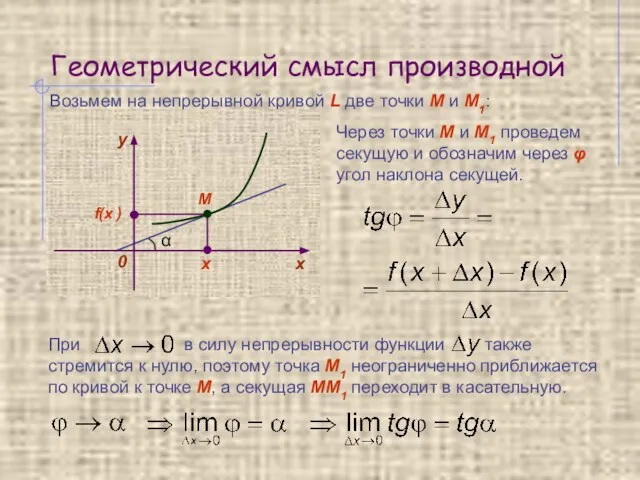
- 4. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 5. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
- 6. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 7. Производные основных элементарных функций 1 Формула бинома Ньютона: Степенная функция: K – факториал
- 8. Производные основных элементарных функций По формуле бинома Ньютона имеем: Тогда:
- 9. Производные основных элементарных функций 2 Логарифмическая функция: Аналогично выводятся правила дифференцирования других основных элементарных функций.
- 10. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 11. Производная сложной функции Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 12. Пример Вычислить производную функции
- 13. Пример Вычислить производную функции Данную функцию можно представить следующим образом: Коротко:
- 14. Производная неявно заданной функции Если функция задана уравнением y = f(х) , разрешенным относительно y, то
- 15. Логарифмическое дифференцирование В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат
- 17. Скачать презентацию







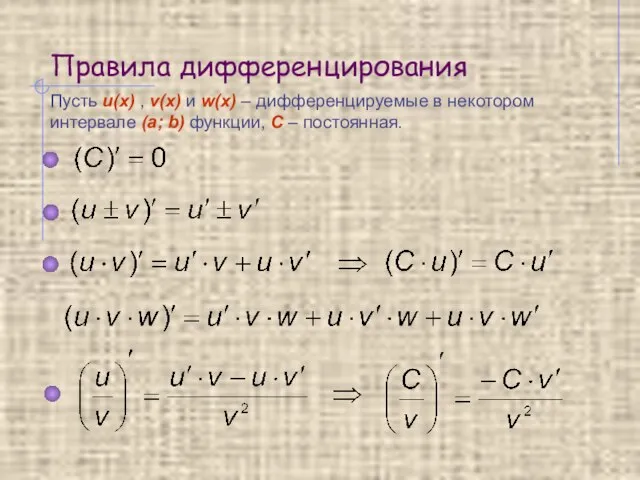





 Классическое определение вероятности
Классическое определение вероятности Симметрия. Закономерности
Симметрия. Закономерности Волшебные палочки. Головоломки
Волшебные палочки. Головоломки Решение графических задач
Решение графических задач Решение квадратных неравенств
Решение квадратных неравенств Профессиональная задача на определение стоимости услуг за перевозку
Профессиональная задача на определение стоимости услуг за перевозку Несократимые дроби
Несократимые дроби Движение. Тест № 6. 9 класс
Движение. Тест № 6. 9 класс Цилиндр, конус, шар
Цилиндр, конус, шар Сравни площади фигур на глаз
Сравни площади фигур на глаз Презентация на тему Тетраэдр
Презентация на тему Тетраэдр  Высоты треугольников
Высоты треугольников Параллельность прямых
Параллельность прямых Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Статистика. Введение в теорию вероятности. Основные понятия
Статистика. Введение в теорию вероятности. Основные понятия Плазма крови, белковый состав плазмы. Группы крови – системы АВ0 и Rh- фактор
Плазма крови, белковый состав плазмы. Группы крови – системы АВ0 и Rh- фактор Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) Презентация на тему Типы параллелепипеда
Презентация на тему Типы параллелепипеда  Периметр, площадь, объём
Периметр, площадь, объём Проверка статистических гипотез. Версия 2
Проверка статистических гипотез. Версия 2 Квадратичная функция
Квадратичная функция Делители и кратные
Делители и кратные Соотношения между элементами прямоугольного треугольника
Соотношения между элементами прямоугольного треугольника Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Решение уравнений с переменной под знаком модуля
Решение уравнений с переменной под знаком модуля Решение тригонометрических уравнений
Решение тригонометрических уравнений Презентация на тему Определение подобных треугольников (8 класс)
Презентация на тему Определение подобных треугольников (8 класс)