Теорема о прямой, перпендикулярной к плоскости

Теорема.
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Обратная теорема.
Если две прямые перпендикулярны к плоскости, то они параллельны.

Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная данной прямой;
Доказательство:
1. α, β:
M
a

Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
a
M
b
O
c

Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
5.
⟹
b
c
a
M
O

Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Доказательство:
m
A

Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Доказательство:
m
n
A
p
⟹
⟹
⟹
⟹
⟹
противоречие
⟹

Задача.
Дано:
AD = 16 см;
Решение:
прямоугольник АВСD;
АА1 ∥ ВВ1;
АА1 ⊥ AB;
АА1 ⊥ AD;
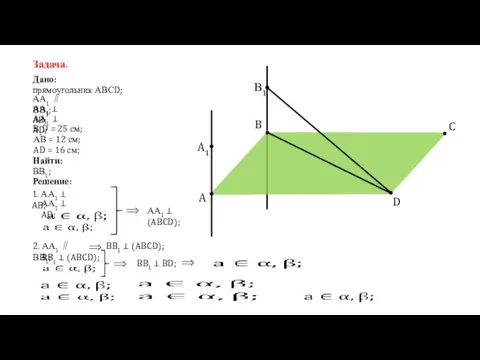
В1D = 25 см;
АВ = 12 см;
Найти:
ВВ1;
A
B
C
D
В1
A1
1. АА1 ⊥ AB;
АА1 ⊥ AD;
⟹
АА1 ⊥ (ABCD);
2. АА1 ∥ ВВ1;
⟹
BB1 ⊥ (ABCD);
BB1 ⊥ (ABCD);
⟹
BB1 ⊥ BD;
⟹

Задача.
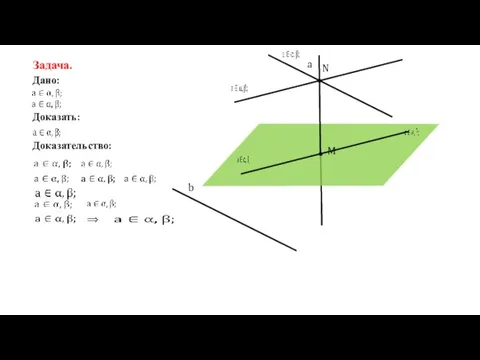
Дано:
Доказательство:
Доказать:
M
a
b
N
⟹