Слайд 2Вписанная окружность
Задача:
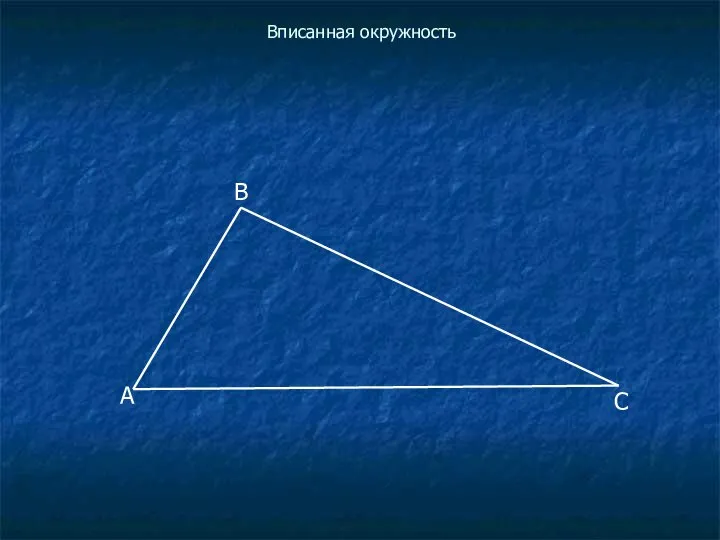
В данный треугольник
вписать окружность.
Слайд 3Вписанная окружность
Из данных рисунков выберете те, на которых, по вашему мнению, изображена
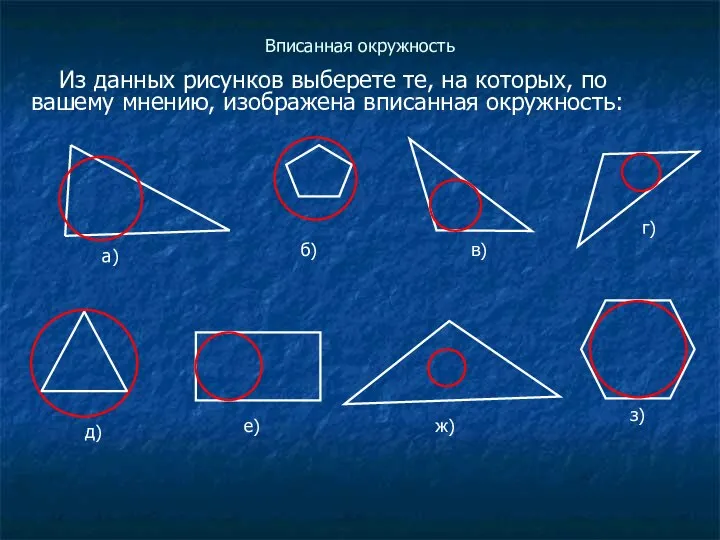
вписанная окружность:
д)
б)
в)
г)
е)
ж)
а)
з)
Слайд 4Вписанная окружность
Определение:
Окружность называется вписанной в многоугольник, если она касается всех его сторон.

Слайд 5Вписанная окружность
Из данных рисунков выберете те, на которых, по вашему мнению, изображена
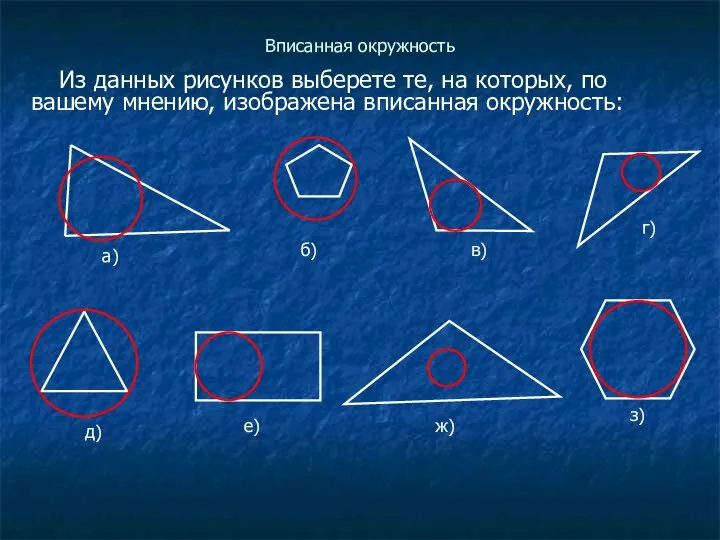
вписанная окружность:
д)
б)
в)
г)
е)
ж)
з)
Слайд 6Вписанная окружность
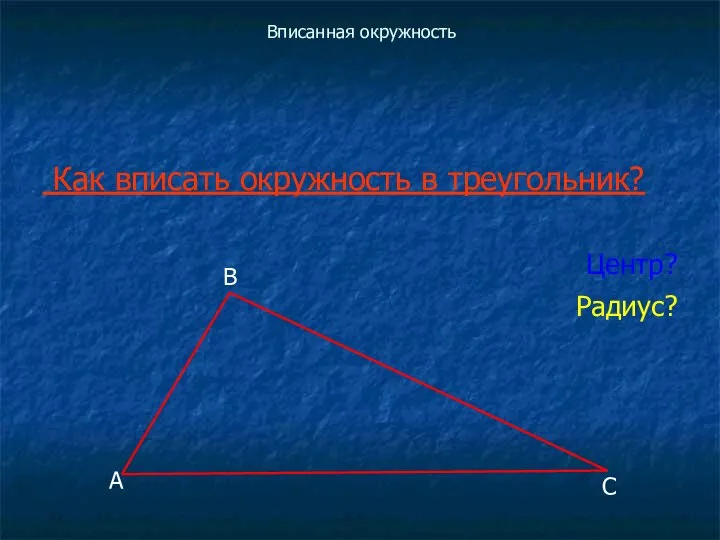
Как вписать окружность в треугольник?
Центр?
Радиус?
А
В
С
Слайд 7Вписанная окружность
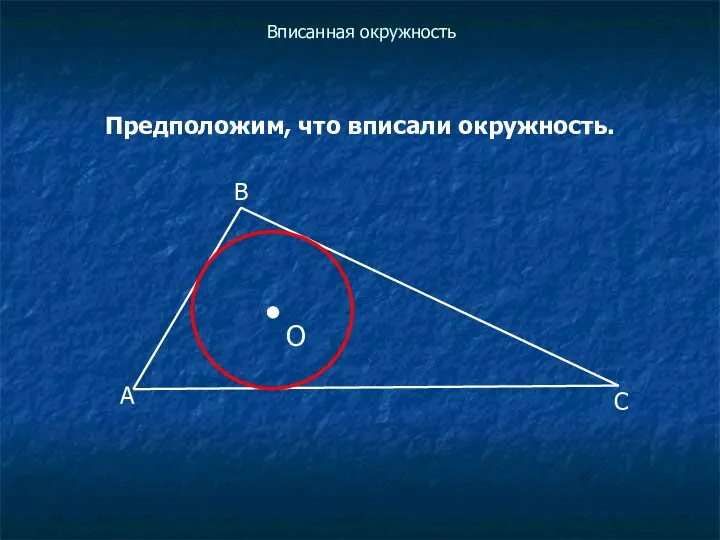
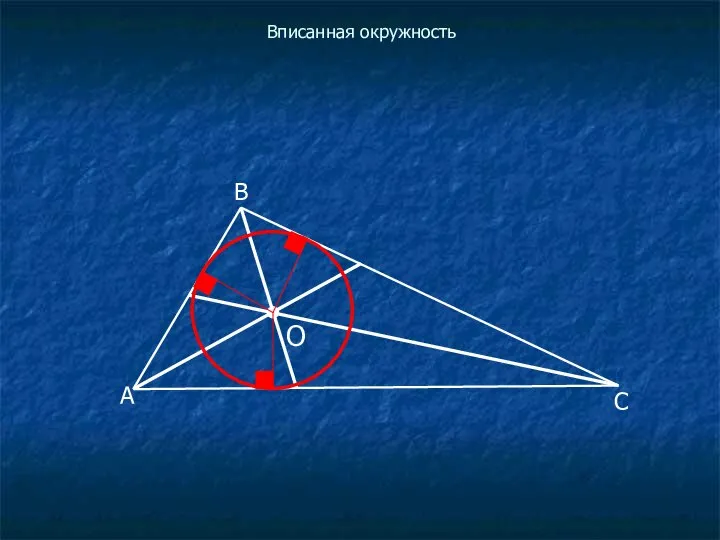
Предположим, что вписали окружность.
Слайд 8Вписанная окружность
О
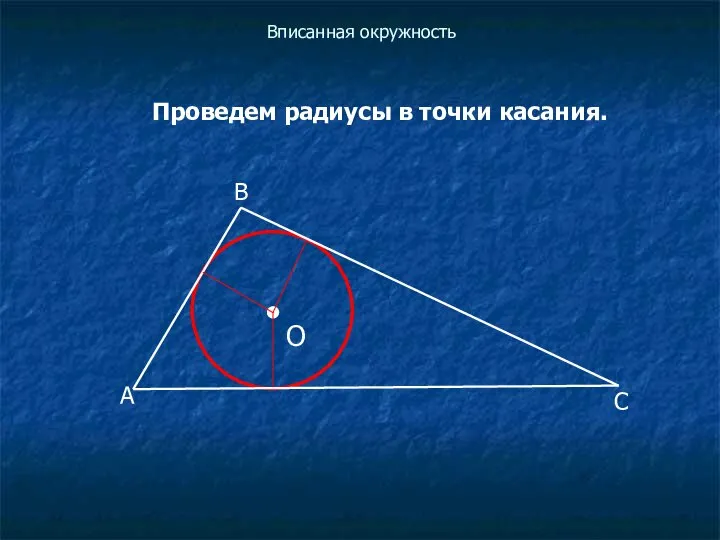
Проведем радиусы в точки касания.
Слайд 11Вписанная окружность
О
АО - биссектриса угла А
ВО - биссектриса угла
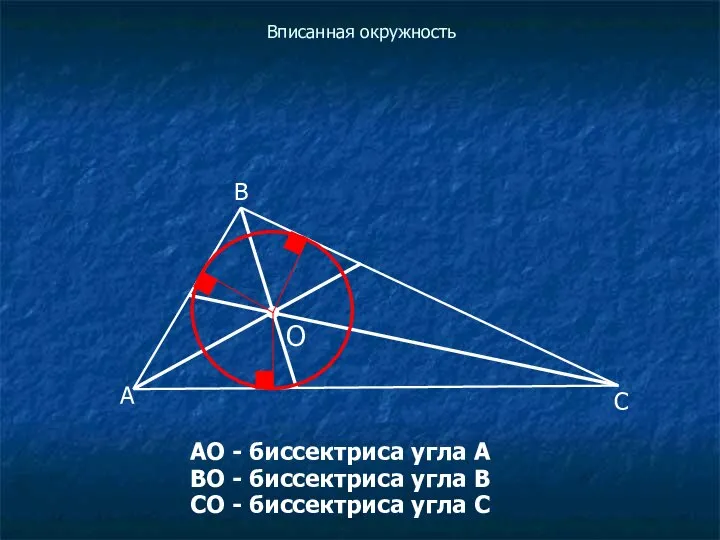
В
СО - биссектриса угла С
Слайд 12Вписанная окружность
Таким образом,
центр вписанной окружности – это точка пересечения биссектрис треугольника,

радиус – это расстояние от центра окружности до сторон треугольника.
Слайд 13Вписанная окружность
Для того, чтобы вписать окружность в треугольник, надо:
1). Найти точку пересечения

биссектрис треугольника (центр окружности);
2). Опустить перпендикуляры из центра окружности к сторонам треугольника (радиус окружности);
3). Провести окружность.
Слайд 15Вписанная окружность
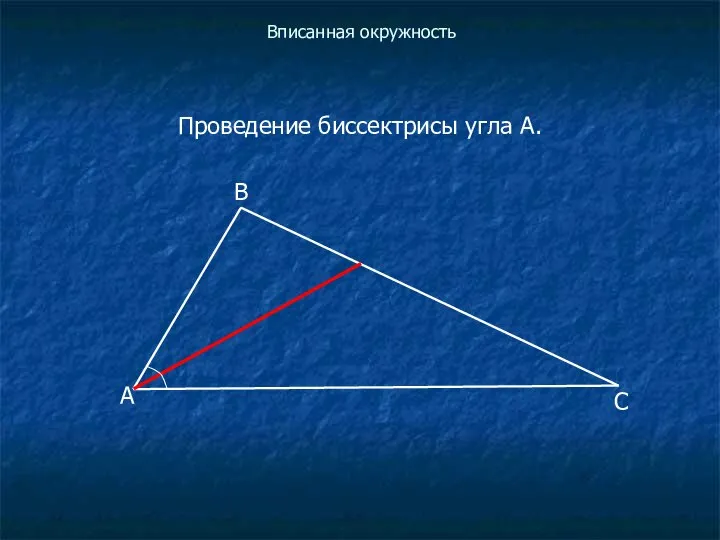
Проведение биссектрисы угла А.
Слайд 16Вписанная окружность
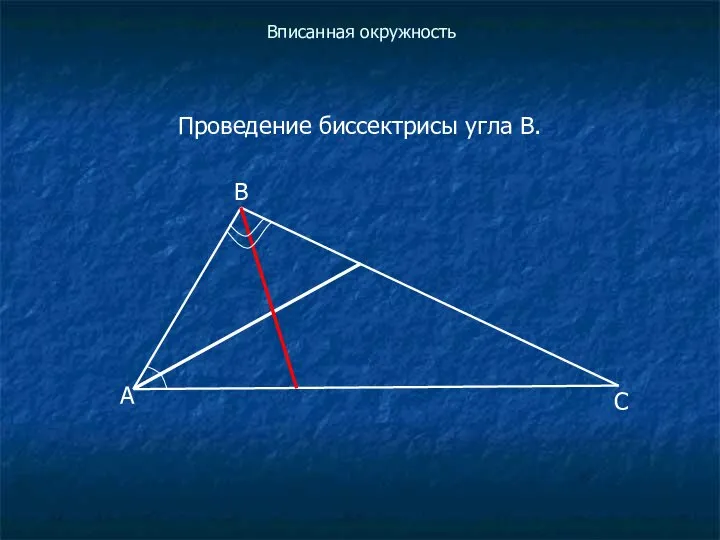
Проведение биссектрисы угла В.
Слайд 17Вписанная окружность
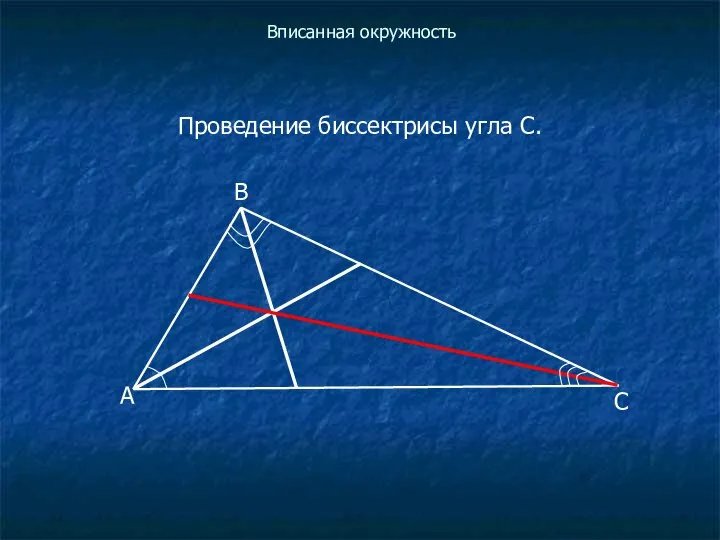
Проведение биссектрисы угла С.
Слайд 18Вписанная окружность
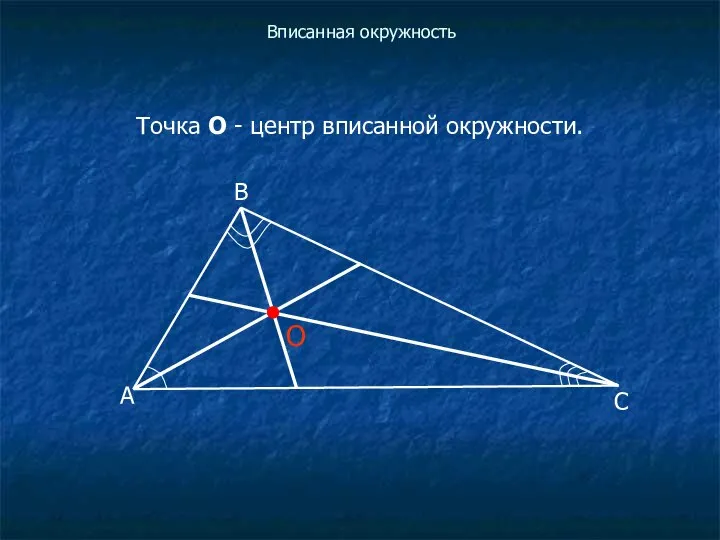
Точка О - центр вписанной окружности.
О
Слайд 19Вписанная окружность
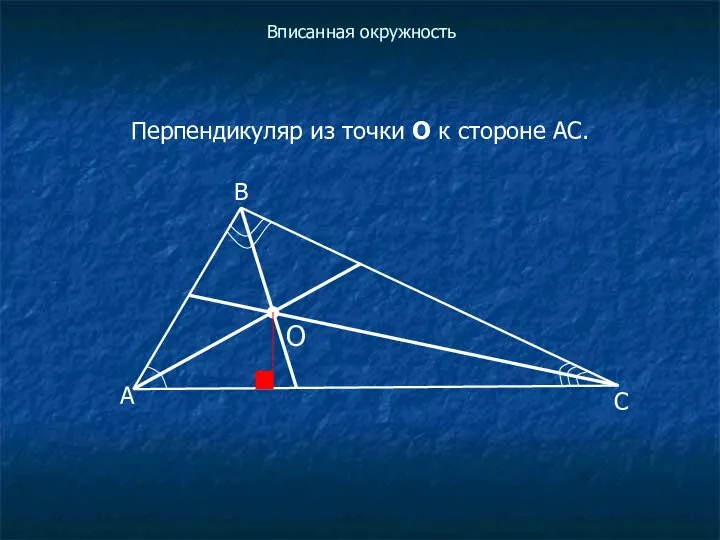
Перпендикуляр из точки О к стороне АС.
Слайд 20Вписанная окружность
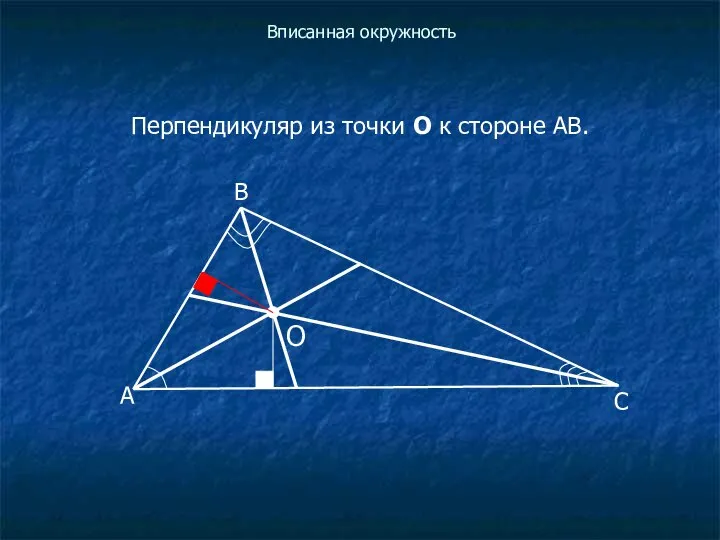
Перпендикуляр из точки О к стороне АВ.
Слайд 21Вписанная окружность
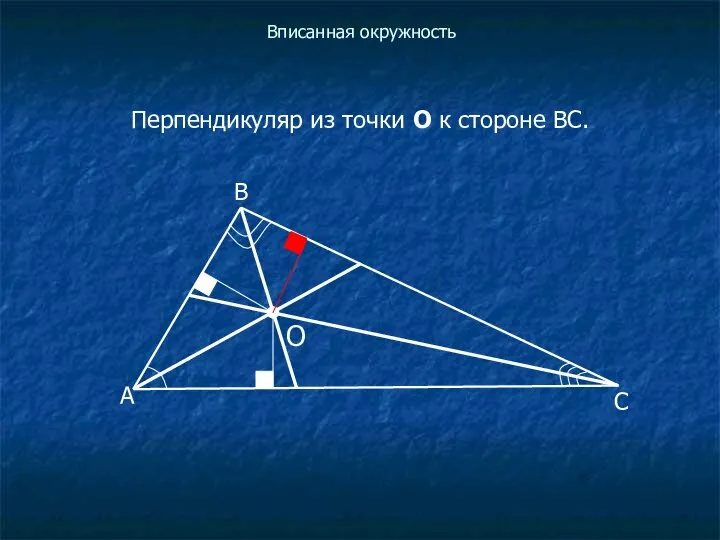
Перпендикуляр из точки О к стороне ВС.
Слайд 22Вписанная окружность
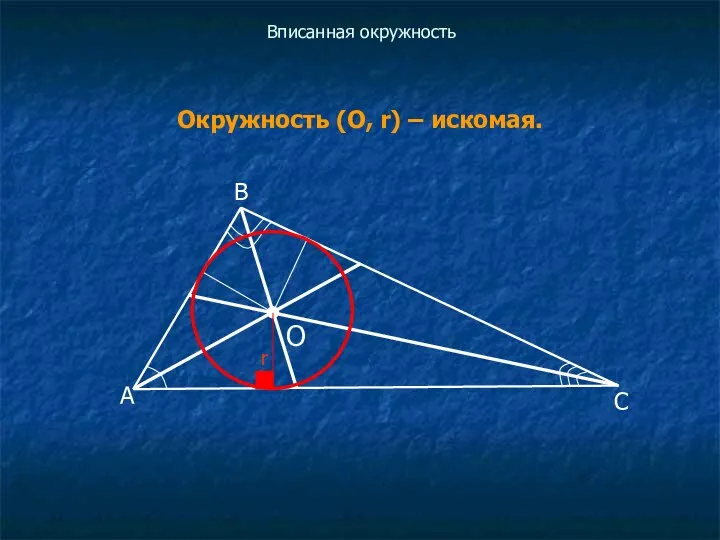
Окружность (О, r) – искомая.
r


















 Многогранники и их основные свойства
Многогранники и их основные свойства Формула сложных процентов в ЕГЭ. 11 класс
Формула сложных процентов в ЕГЭ. 11 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Практика. Дискретная математика
Практика. Дискретная математика Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Уравнение прямой
Уравнение прямой Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Координаты вектора
Координаты вектора Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Классификация многоугольников по числу углов
Классификация многоугольников по числу углов Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов  Переместительное свойство умножения
Переместительное свойство умножения Свойства умножения. 5 класс
Свойства умножения. 5 класс Математический турнир Умники и умницы
Математический турнир Умники и умницы Исследование операций. Принятие решений и неопределенность. Лекция 3
Исследование операций. Принятие решений и неопределенность. Лекция 3 11 клас призма
11 клас призма Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений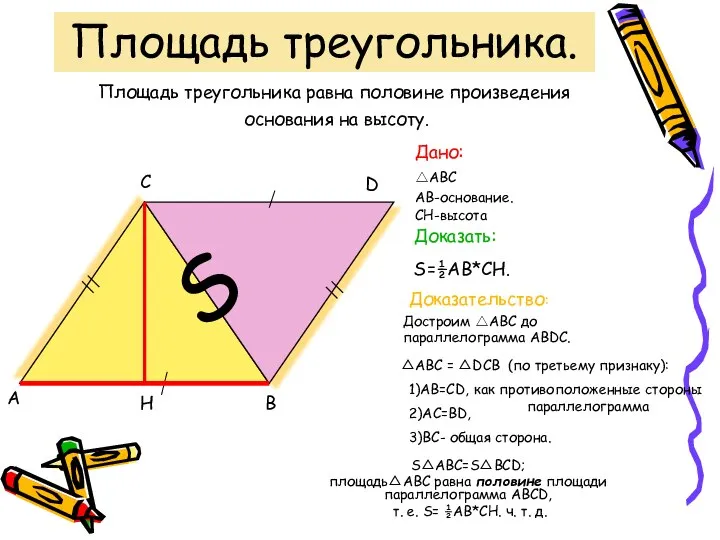 Площадь треугольника
Площадь треугольника Параллельные прямые
Параллельные прямые Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Корень n-ой степени
Корень n-ой степени Шестое математическое действие
Шестое математическое действие Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование