Содержание
- 2. Лекция №7.1 План 1. Возникновение теории графов. 2. Основные понятия и определения теории графов. 3.
- 3. Задачи, приводящие к понятию графа Теория графов – это раздел дискретной математики, особенностью которого является геометрический
- 4. Задачи, приводящие к понятию графа Подобные схемы впервые назвал «графами» венгерский математик Денеш Кёниг в 1936
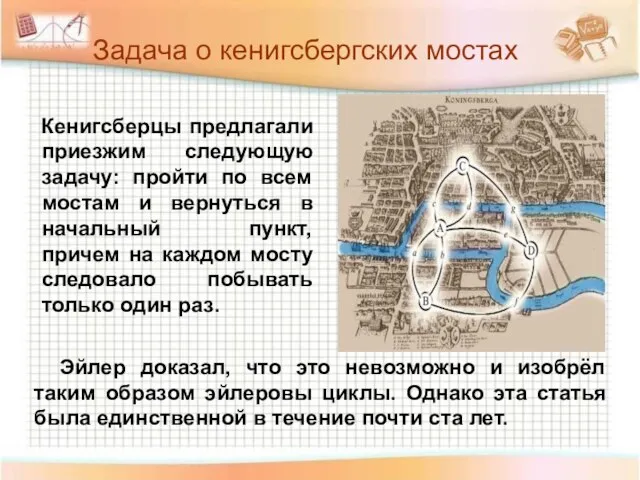
- 5. Задача о кенигсбергских мостах Кенигсберцы предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в
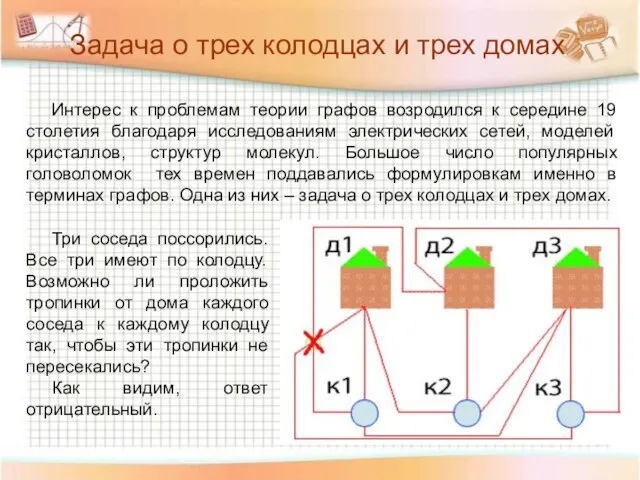
- 6. Интерес к проблемам теории графов возродился к середине 19 столетия благодаря исследованиям электрических сетей, моделей кристаллов,
- 7. Теорема о четырёх красках — утверждение о том, что всякую расположенную на сфере карту можно раскрасить
- 8. Период интенсивной разработки общей теории графов начался в 50-х годах ХХ века в связи со становлением
- 9. Применение графов Графы применяются: Банковское дело Промышлен-ность Медицина Молекулярная биология
- 10. Лекция доктора технических наук, профессора Владимира Алексеевича Кузнецова Петрозаводский государственный университет (РФ) .
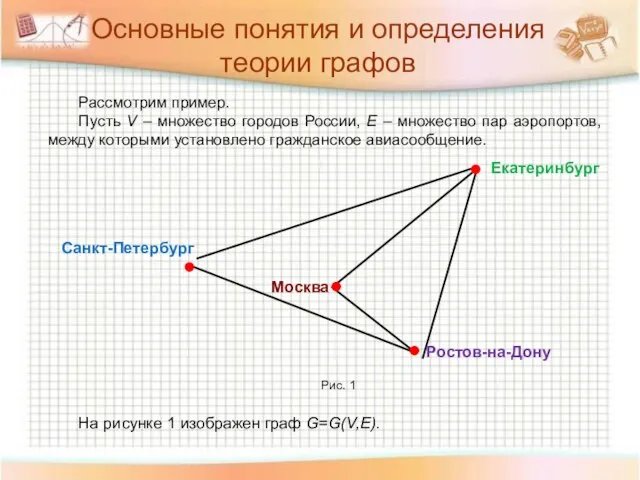
- 11. Рассмотрим пример. Пусть V – множество городов России, Е – множество пар аэропортов, между которыми установлено
- 12. Определение графа Пусть V - непустое множество, состоящее из соединенных некоторым образом точек Xi. Множество V
- 13. Определение графа Ребро u=(Xi, Xj) называется неориентированным, если (Xi, Xj) = (Xj, Xi). Ребро u=(Xi, Xj)
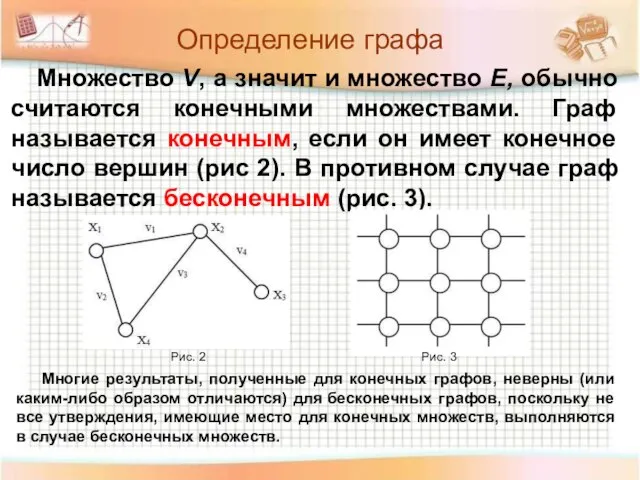
- 14. Определение графа Множество V, а значит и множество E, обычно считаются конечными множествами. Граф называется конечным,
- 15. Определение графа Вершины и рёбра графа называются также элементами графа, число вершин в графе, т.е. |V|
- 16. Определение графа Две концевые вершины одного и того же ребра называются смежными. Если u =(Xi, Xj),
- 17. Определение графа Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды). Обозначают: ρ(Xi).
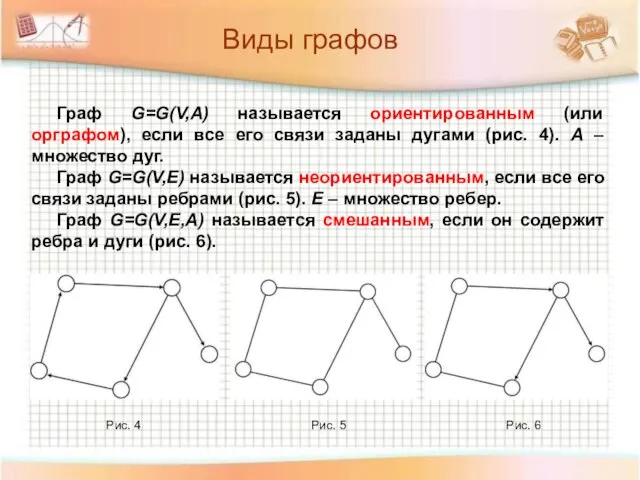
- 18. Виды графов Граф G=G(V,A) называется ориентированным (или орграфом), если все его связи заданы дугами (рис. 4).
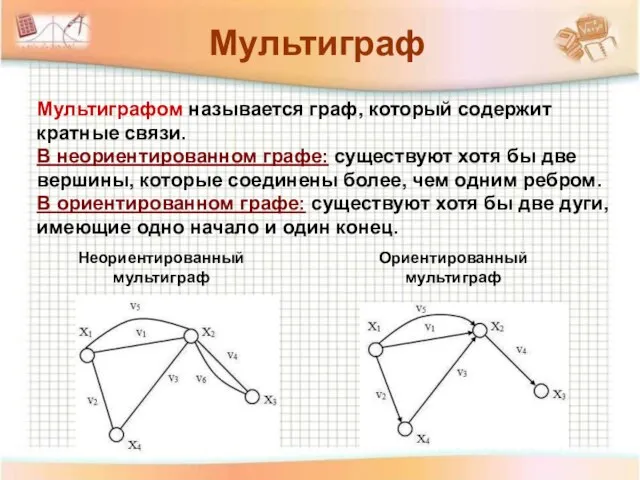
- 19. Мультиграфом называется граф, который содержит кратные связи. В неориентированном графе: существуют хотя бы две вершины, которые
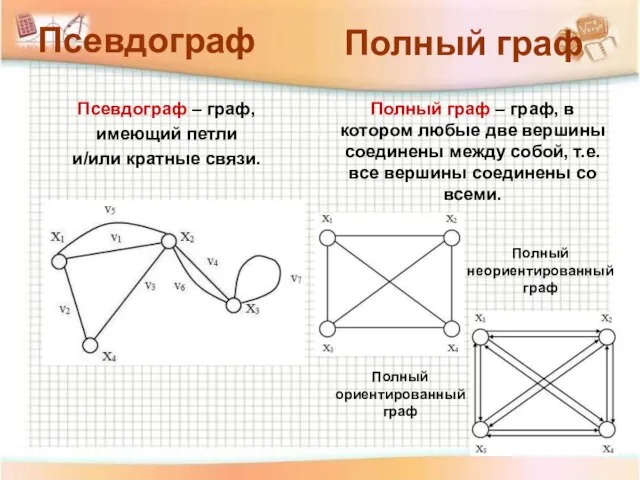
- 20. Псевдограф – граф, имеющий петли и/или кратные связи. Полный граф – граф, в котором любые две
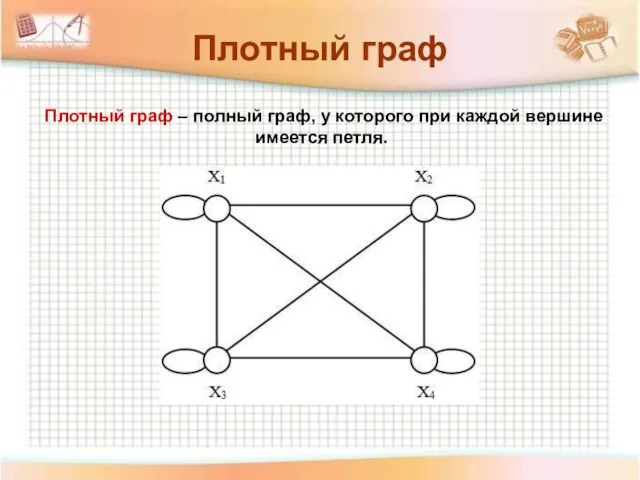
- 21. Плотный граф – полный граф, у которого при каждой вершине имеется петля. Плотный граф
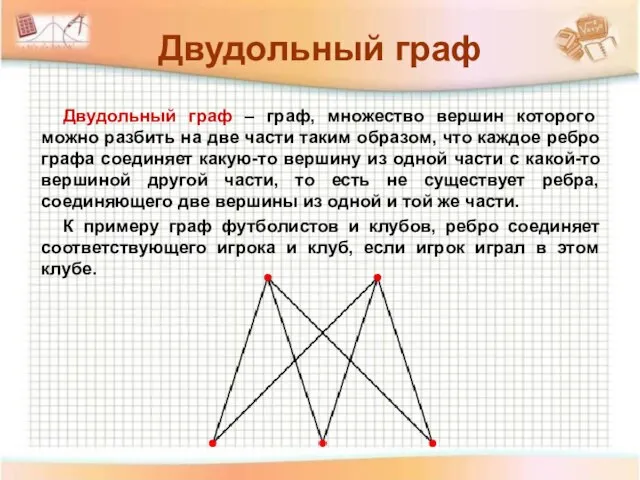
- 22. Двудольный граф – граф, множество вершин которого можно разбить на две части таким образом, что каждое
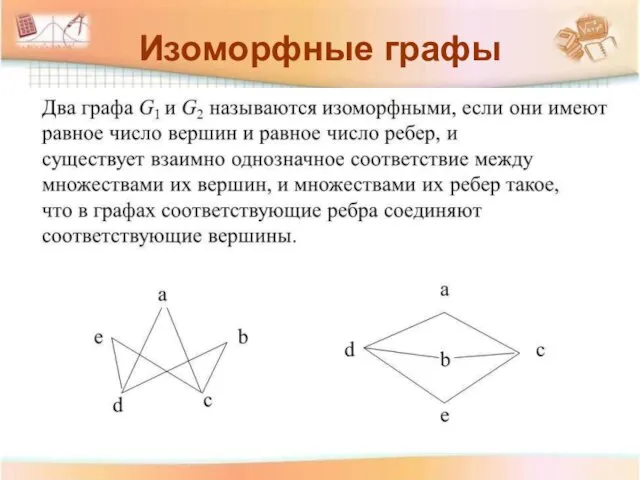
- 23. Изоморфные графы
- 24. Способы задания графов Геометрический. Пусть задан граф G=G(X,V). Графы имеют наглядную геометрическую интерпретацию в виде диаграмм,
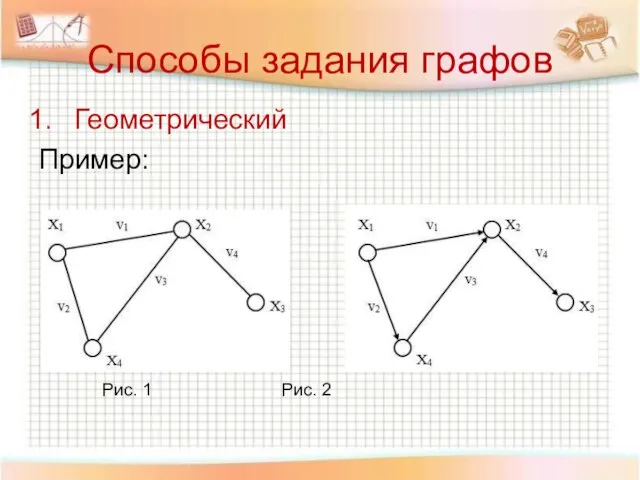
- 25. Способы задания графов Геометрический Пример: Рис. 1 Рис. 2
- 26. Способы задания графов Аналитический. Всякий граф G=G(X,V) можно рассматривать как совокупность множества элементов X и подмножества
- 27. Способы задания графов Аналитический. Чтобы задать граф аналитически, необходимо указать: Множество вершин X. Множество ребер (дуг)
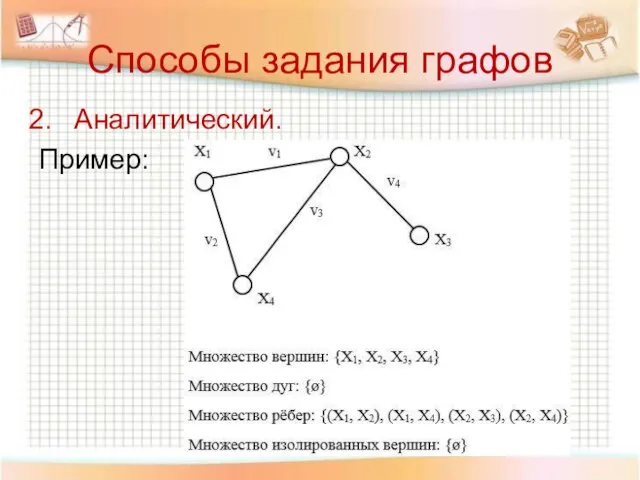
- 28. Способы задания графов Аналитический. Пример:
- 30. Скачать презентацию














 Координаты середины отрезка. Задачи
Координаты середины отрезка. Задачи Математическая вертикаль. Текстовые задачи
Математическая вертикаль. Текстовые задачи Презентация на тему Логарифмическая функция в уравнениях
Презентация на тему Логарифмическая функция в уравнениях 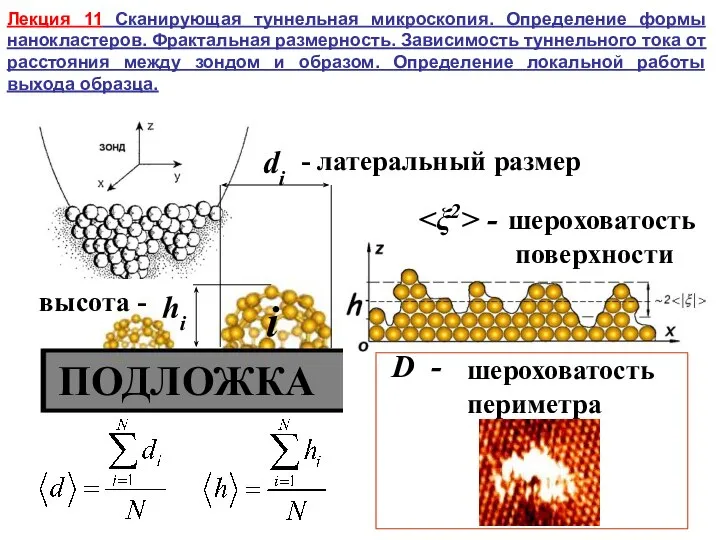 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Неполные квадратные уравнения
Неполные квадратные уравнения Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Группы по одному или нескольким признакам
Группы по одному или нескольким признакам О математике на разных языках
О математике на разных языках Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Степень с отрицательным показателем
Степень с отрицательным показателем Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса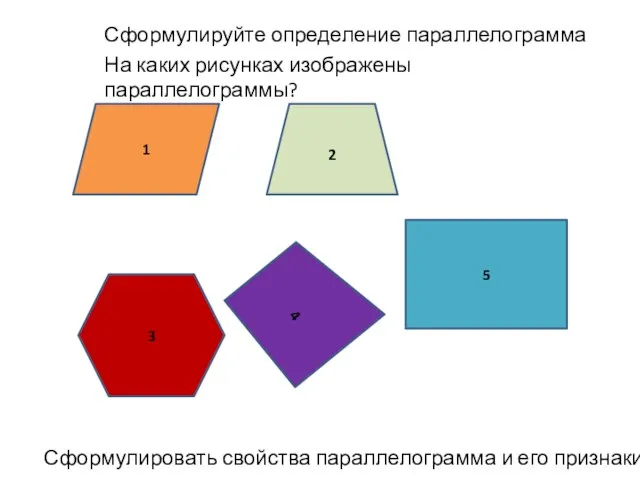 Презентация на тему Параллелограмм и трапеция
Презентация на тему Параллелограмм и трапеция 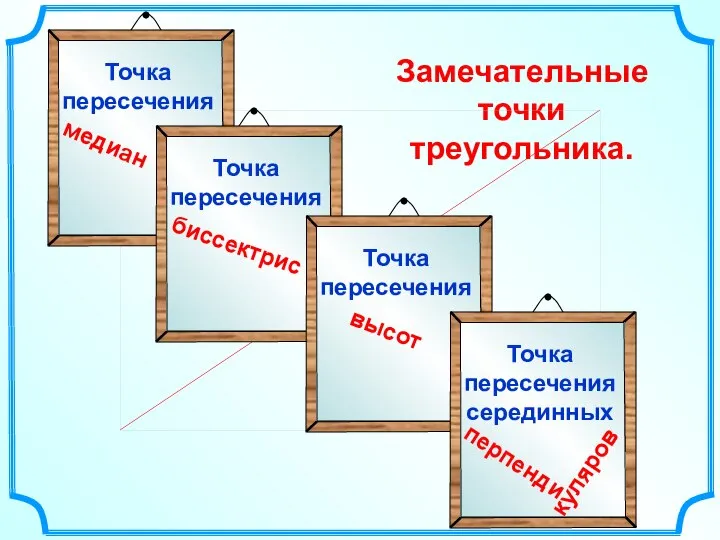 Замечательные точки треугольника
Замечательные точки треугольника Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Презентация на тему Измеряем длину окружности
Презентация на тему Измеряем длину окружности  Первый признак параллельности прямых
Первый признак параллельности прямых برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد
برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد Состав числа 3
Состав числа 3 Построение сечений
Построение сечений История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Основные правила дифференцирования
Основные правила дифференцирования Рисуем с помощью координат
Рисуем с помощью координат Секреты решения тестовых заданий по математике
Секреты решения тестовых заданий по математике Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Элементы уроков с применением интерактивной доски
Элементы уроков с применением интерактивной доски Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс)
Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс) Векторный анализ - теория поля. Векторное поле. Лекция 17
Векторный анализ - теория поля. Векторное поле. Лекция 17 Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число