Кривая Лоренца. Решение задач

Условие задачи
В деревне живут четыре семьи, которые получают следующие доходы:
Ивановы – 10 тыс. рублей в месяц
Петровы – 20 тыс. рублей в месяц
Сидоровы – 30 тыс. рублей в месяц
Васечкины – 40 тыс. рублей в месяц
Постройте кривую Лоренца для деревни.
Рассчитайте индекс Джини.

Решение задачи
1) Найдем общую сумму доходов всех семей данной деревни:
Обозначим доход буквой Y
∑ Y = Y1 + Y2 + Y3 +Y4
∑ Y = 10 + 20 + 30 + 40 = 100 тыс. руб. мес.

2) Определим, сколько в процентах получает каждая семья доходов от суммарного дохода деревни.
Примем общий доход деревни за 100%. Тогда:
Ивановы – 10% Y
Петровы – 20% Y
Сидоровы – 30% Y
Васечкины – 40% Y

3) Определим, сколько процентов от всего населения деревни составляет каждая семья.
Обозначим население буквой N
Примем всё население деревни за 100%, тогда:
Ивановы – 25% N
Петровы – 25% N
Сидоровы – 25% N
Васечкины – 25% N

4) Соотнесём % дохода семьи с % от общего населения.
Ивановы – 10% Y – 25% N
Петровы – 20% Y – 25% N
Сидоровы – 30% Y – 25% N
Васечкины – 40% Y – 25% N

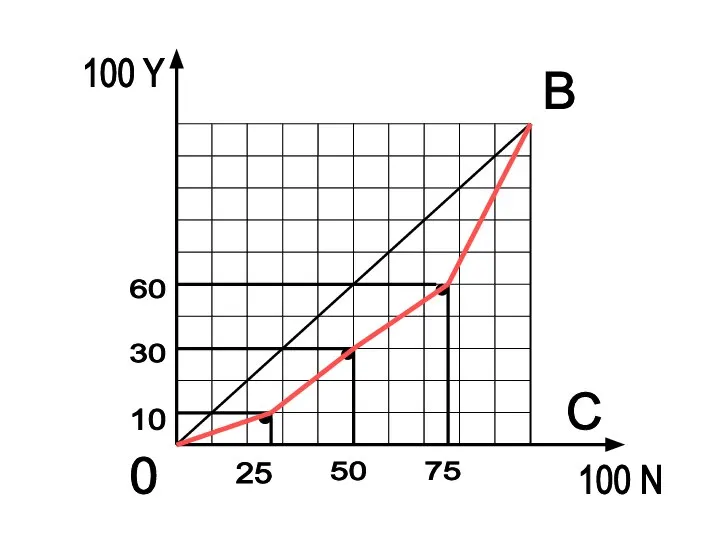
5) На основании полученных результатов построим кривую Лоренца для данной деревни.
Строим сетку:

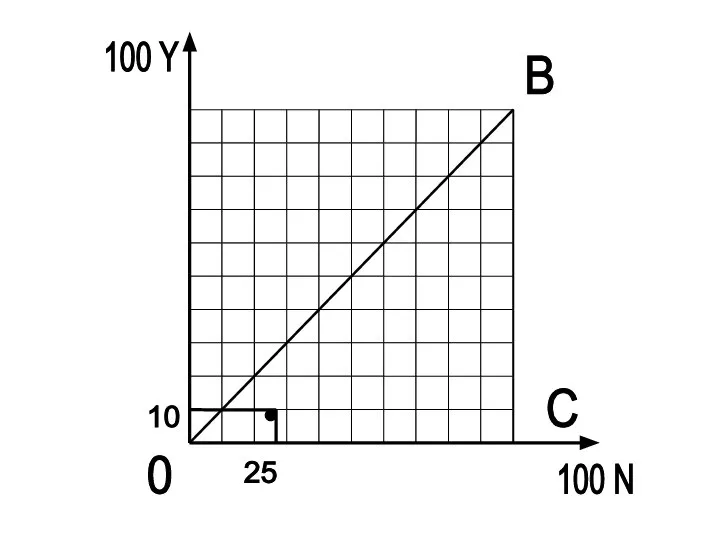
Построение кривой Лоренца начинается с самой малообеспеченной семьи. По условию нашей задачи – это семья Ивановых.
Ивановы – 10% Y – 25% N

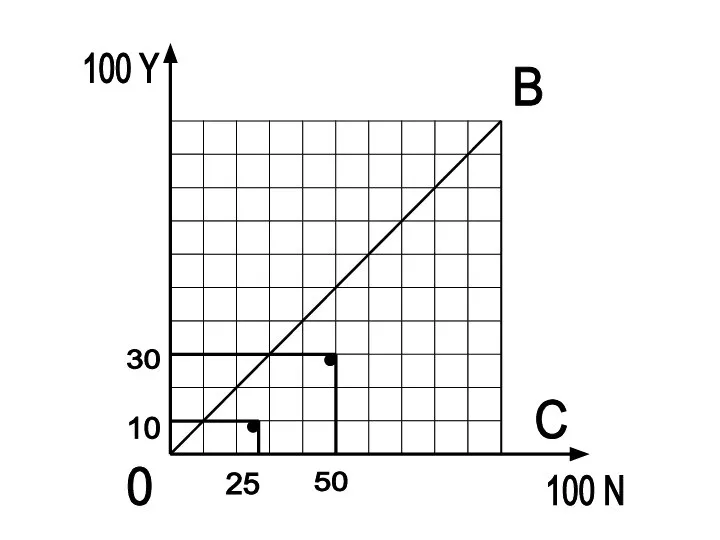
Следующим шагом найдем сколько в % от общего дохода получает семья Ивановых плюс вторая по уровню дохода семья Петровых.
Ивановы – 10% Y – 25% N
Петровы – 20% Y – 25% N
Всего: - 30 % Y – 50% N

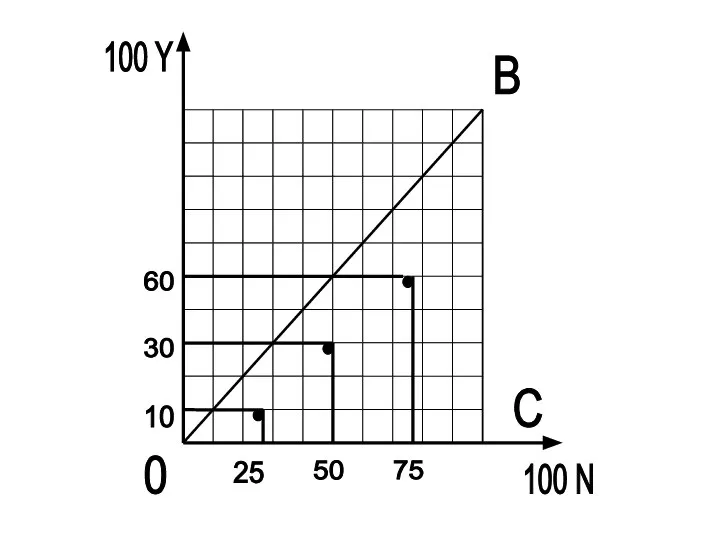
Затем по тому же принципу рассчитаем:
Ивановы – 10% Y – 25% N
Петровы – 20% Y – 25% N
Сидоровы – 30% Y – 25% N
Всего: – 60% Y – 75% N

Построим кривую Лоренца для данной деревни

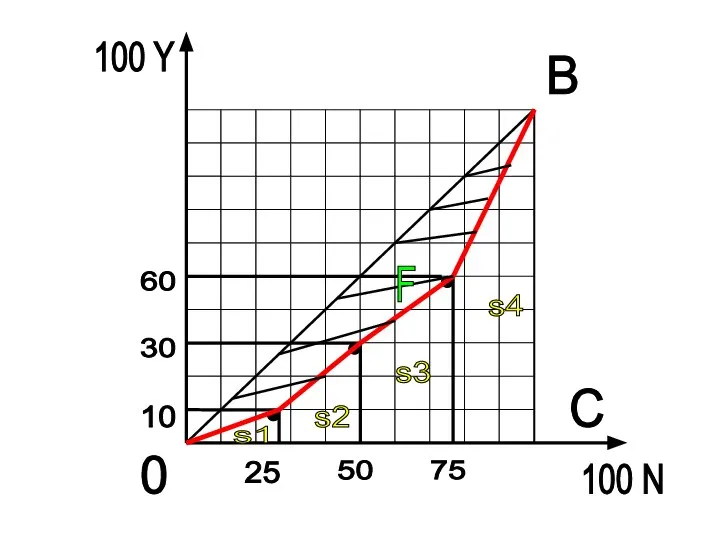
Рассчитаем индекс Джини
9) Обозначим индекс Джини буквой G:
G = s F
s∆ OBC
10) Площадь фигуры F:
s F = s∆ OBC - ∑ S

12) Рассчитаем площадь фигуры F:
∑ S = S1 + S2 + S3 + S4
S1 = (a × b) : 2 = (10 × 25) : 2 =
S2 = 1 (a+ b) × h
2
S2 = 1 (10+ 30) × 25 =
2

S3 = 1 (30+ 60) × 25 =
2
S4 = 1 (60+ 100) × 25 =
2
∑ S = S1 + S2 + S3 + S4
∑ S =
s F = 5000 - =

13) Рассчитаем индекс Джини:
G = s F
s∆ OBC
G = s F =
5000