Задачи на построение примера. Геометрические конструкции

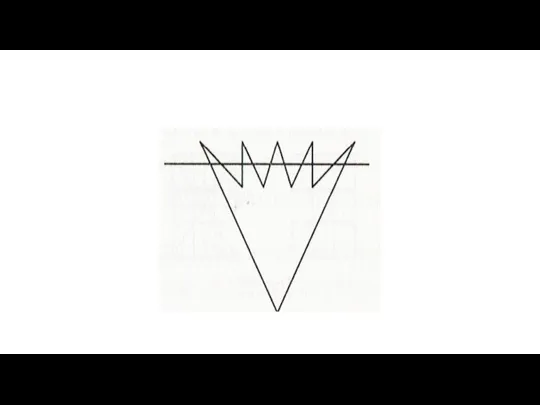
Задача 2
Зачеркните все 16 точек, изображённых на рисунке, шестью отрезками, не отрывая карандаша от бумаги и не проводя отрезков по линиям сетки.

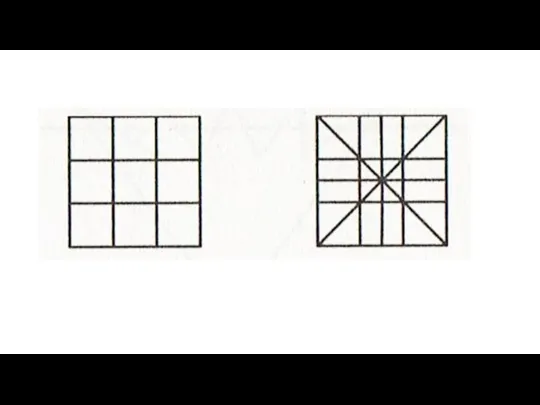
Задача 3
Разделите квадрат 3 х 3 на 8 равных частей

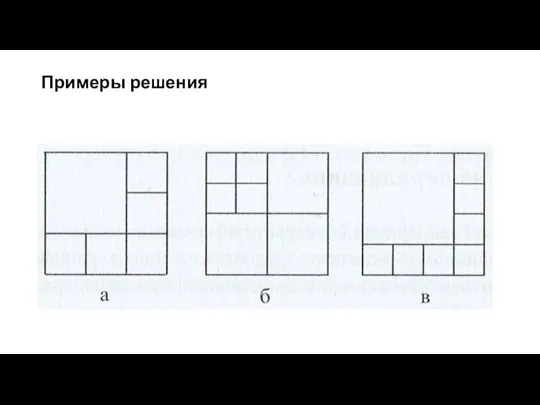
Задача 4
Разрежьте квадрат на:
а) 6 квадратов;
6)7 квадратов;
в) 8 квадратов.
На любое ли количество квадратов, большее 8, можно разрезать квадрат?

Примеры решения

Задача 5
Разложите 8 монет в центры клеток доски 4x4, чтобы ни на какой прямой не лежали 3 монеты (монеты считать точечными). Докажите, что 9 монет таким образом разложить нельзя.

Задачи на переливания
Задача 6
Можно ли, имея лишь два сосуда 4 и 3 л, набрать из водопроводного крана ровно 1 л воды?

Задача 7
Можно ли, имея лишь два сосуда 3 и 5 л, набрать из водопроводного крана ровно 4 л воды?

Задачи на взвешивания
При решении задач на взвешивания полное решение задачи должно содержать рассмотрение всех возможных вариантов.
Задача 8
Среди девяти монет одна — фальшивая. Она отличается от настоящих монет весом, известно, что она легче настоящих. Как при помощи двух взвешиваний на чашечных весах без гирь обнаружить фальшивую монету?

Задача 9
Имеются 3 мешочка, в каждом по 50 монеток. В одном из них все монетки весят по 9 г, во втором — по 10 г, в третьем — по 11 г. Гном хочет определить, где какой мешочек, при помощи весов, которые умеют определять вес положенного на них груза, но ломаются от веса 50 г и больше. Как ему это сделать за одно взвешивание, не ломая весы?

Задача 10
Среди четырёх монет одна — фальшивая. Она отличается от настоящих монет весом, однако неизвестно, легче она или тяжелее настоящих. Масса настоящей монеты 5 г. Имеется одна гиря массой 5 г. Как при помощи двух взвешиваний на чашечных весах обнаружить фальшивую монету и определить, легче она или тяжелее настоящих?

Построение алгоритма, задачи с числами
Задача 11
В клетки таблицы по некоторому правилу записали несколько чисел. Определите, что эго за правило, и заполните три последние клетки таблицы.

Задача 12
Старейший магический квадрат был составлен в Китае. Первое изображение на черепаховом панцире датируется 2200 г. до н.э. В девяти клетках этого квадрата вписаны числа от 1 до 9.
Другой магический квадрат был составлен в Индии в I в. н. э. Сравните суммы чисел в строчках, столбцах и диагоналях квадратов и скажите, в чём заключается магическое свойство этих квадратов.
Рис.1
Рис.2

Задача 13
Можно ли в таблице 3x3, следуя шахматным правилам, конём:
а) попасть из угловой клетки в диагонально противоположную;
б) обойти все клетки доски?

Задача 14
Существует ли шесть различных ненулевых действительных чисел, чья сумма равна их произведению?