Математика вокруг нас

Здравствуйте, ребята. Сегодня мы с вами будем работать с лабиринтами

ЛАБИРИНТЫ
История и математика

ПЕРВЫЕ ЛАБИРИНТЫ
Первые похожие на лабиринт наскальные рисунки появились на Земле еще в каменном веке. Трудно сказать, что имел в виду доисторический художник, высекая извилистые линии и спирали, но идея передавалась сквозь века, превратившись наконец в глобальный символ — семь линий, закрученных вокруг центра. Древнейшим из найденных считают знак лабиринта, нацарапанный на стене усыпальницы в Луззанасе на острове Сардиния, возведенной как минимум четыре тысячи лет назад.

ПЕТРОГЛИФЫ
Большинство древних «классических» лабиринтов создавалось по одинаковому, вполне определенному шаблону с одной-единственной очень извилистой тропой, ведущей от входа к центру. Таковы сохранившиеся до наших дней петроглифы в виде лабиринтов, обнаруженные в Галисии, на северо-западе Испании, и датируемые 2000 годом до н. э., глиняные таблички с изображением лабиринтов, найденные в греческом городе Пилосе, возраст которых 3 000 лет, рисунки лабиринтов, нацарапанные на руинах в турецком Гордионе, относящиеся к 750 году до н. э.

ЛАБИРИНТ МИНОТАВРА
Лабиринт, построенный, по легенде, афинским зодчим Дедалом по приказу царя Миноса, представлял собой подземную сеть туннелей, которые вели в обиталище чудовищного Минотавра. Долгое время считалось, что прообразом знаменитого лабиринта послужили обширные каменоломни, расположенные в окрестностях критского города Гортина. Однако в 1900—1930 годах английский археолог Артур Эванс, проводя раскопки в Кносе, открыл царский дворец колоссальных размеров, основная часть которого была построена более чем за 1 500 лет до н. э.
Сегодня грандиозное сооружение площадью около 16 тыс. м2, интерпретируется археологами как прототип легендарного лабиринта Минотавра.

ЭВАНС, АРТУР ДЖОН (1851-1941)
Человек, нашедший «лабиринт минотавра»

ГОЛОВОЛОМКИ МЭЙЗ
Мейзы по своему строению более изощренные и запутанные фигуры, нежели лабиринты. Как правило, в таких головоломках заложены несколько дорог к цели, два или более входов и выходов, дорожки сообщаются между собой и образуют развилки. Решить мейз, то есть пройти к его центру или какой-либо цели, не так-то просто. Создатели выстроили сложные задачи: выбрать правильный вход, угадать направление на развилке или не попасть дважды на одну и ту же дорожку. Идея мейзов восходит к Средневековью и представляет собой результат освоения математики.

ПАРКОВЫЙ ЛАБИРИНТ
Лабиринты замка Во-Ле-Виконт во Франции

ОХРАННЫЙ ЛАБИРИНТ
По образу лабиринта были построены защитные стены города Шимангада, расположенного в предгорьях Гималаев, на территории современного Непала. Этот неприступный город пал под ударами мусульманских войск в 1325 году только после того, как предатель указал неприятелю слабое место в крепостных стенах. Руины Шимангады сохранились до наших дней, но их почти совсем поглотили джунгли.

УНИКАЛЬНЫЕ ЛАБИРИНТЫ
Фермер Том Пирси (Tom Pearcy) из Йоркшира, Великобритания, соорудил у себя на поле самый большой лабиринт в мире

ЛАБИРИНТ ГОЛОВОЛОМКА

ЛАБИРИНТЫ
Методы решения

МЕТОД ГРАФА
Правило I. Отправляемся от начального пункта (первого перекрестка) и идем по какой угодно дороге, пока не приходим или в тупик, или к новому перекрестку. Тогда:
1. Если окажется, что мы попали в тупик, то возвращаемся назад и пройденный путь должен быть 1 уже отброшен, так как мы его прошли два раза (вперед и обратно).
2. Если же мы приходим к новому перекрестку, то направляемся по новому произвольному пути, не забывая только всякий раз отметить поперечной черточкой путь, по которому мы прибыли, и путь, по которому отправились дальше
Мы следуем указанному выше первому правилу всякий раз, когда приходим на такой перекресток, на котором мы еще не были. Но в конце концов мы должны прийти к перекрестку, на котором мы уже были, и здесь может представиться два случая. На известный уже нам пункт мы приходим по дороге, уже раз пройденной нами, или же по пути новому, не отмеченному еще черточкой. Следует придерживаться таких правил:

МЕТОД ГРАФА
Правило II. Прибыв на известный уже нам перекресток по новой дороге, мы должны сейчас же повернуть обратно, предварительно отметив этот путь двумя черточками (прибытие и обратное отправление)
Правило III. Если мы приходим на известный нам перекресток таким путем, которым уже раз прошли раньше, то, отметив этот путь второй черточкой отправляемся дальше путем, которым мы еще не шли, если только такой путь существует. Но если такого пути нет, то выбираем дорогу, по которой прошли только один раз.

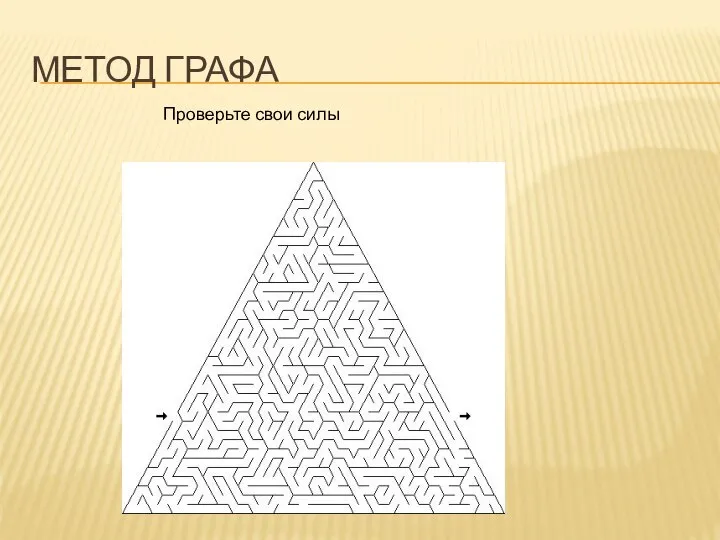
МЕТОД ГРАФА
Проверьте свои силы

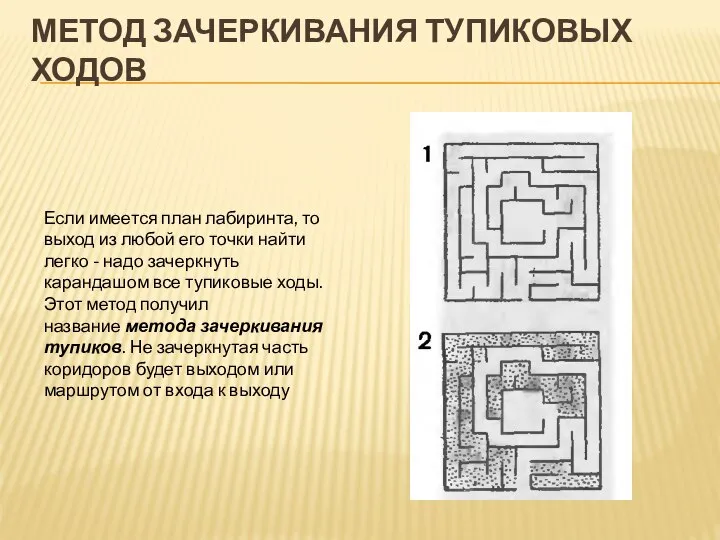
МЕТОД ЗАЧЕРКИВАНИЯ ТУПИКОВЫХ ХОДОВ
Если имеется план лабиринта, то выход из любой его точки найти легко - надо зачеркнуть карандашом все тупиковые ходы. Этот метод получил название метода зачеркивания тупиков. Не зачеркнутая часть коридоров будет выходом или маршрутом от входа к выходу

МЕТОД ЗАЧЕРКИВАНИЯ ТУПИКОВЫХ ХОДОВ
Проверьте свои силы

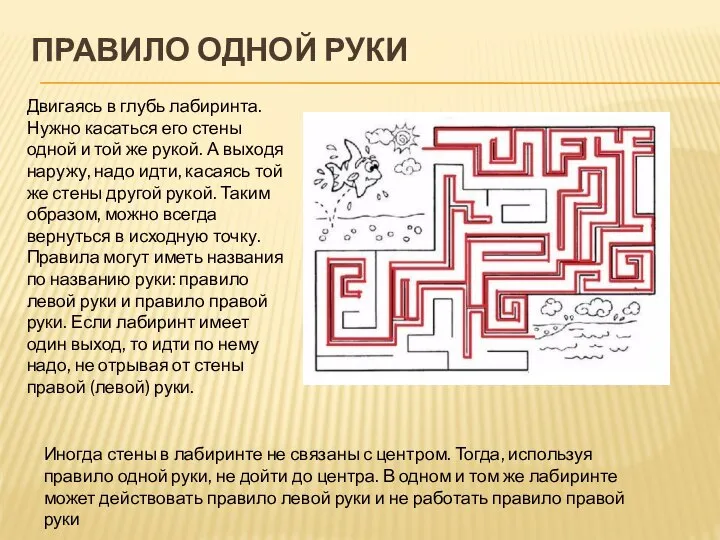
ПРАВИЛО ОДНОЙ РУКИ
Двигаясь в глубь лабиринта. Нужно касаться его стены одной и той же рукой. А выходя наружу, надо идти, касаясь той же стены другой рукой. Таким образом, можно всегда вернуться в исходную точку.
Правила могут иметь названия по названию руки: правило левой руки и правило правой руки. Если лабиринт имеет один выход, то идти по нему надо, не отрывая от стены правой (левой) руки.
Иногда стены в лабиринте не связаны с центром. Тогда, используя правило одной руки, не дойти до центра. В одном и том же лабиринте может действовать правило левой руки и не работать правило правой руки

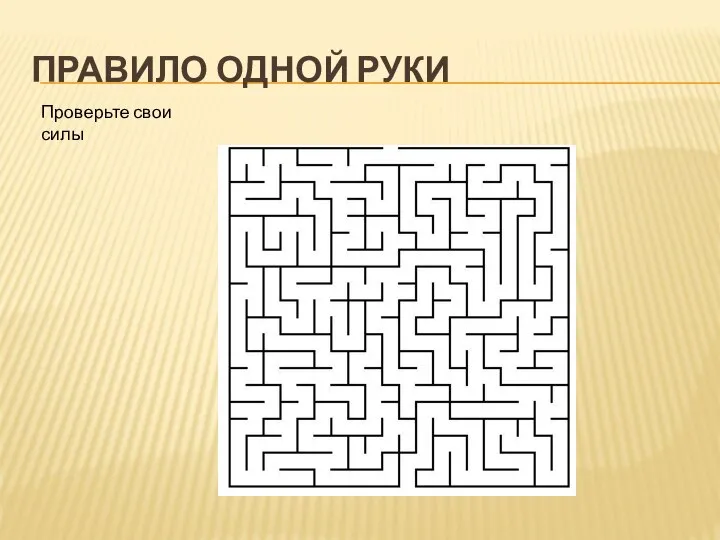
ПРАВИЛО ОДНОЙ РУКИ
Проверьте свои силы

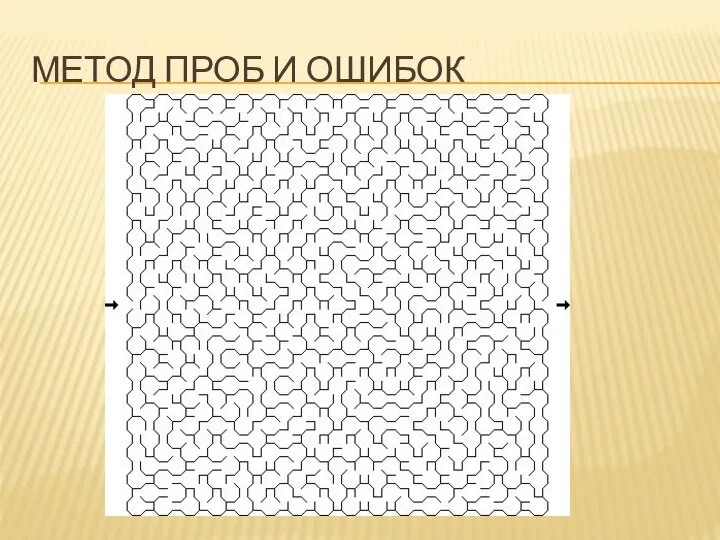
МЕТОД ПРОБ И ОШИБОК

ЛАБИРИНТЫ
Для личной тренировки