Содержание
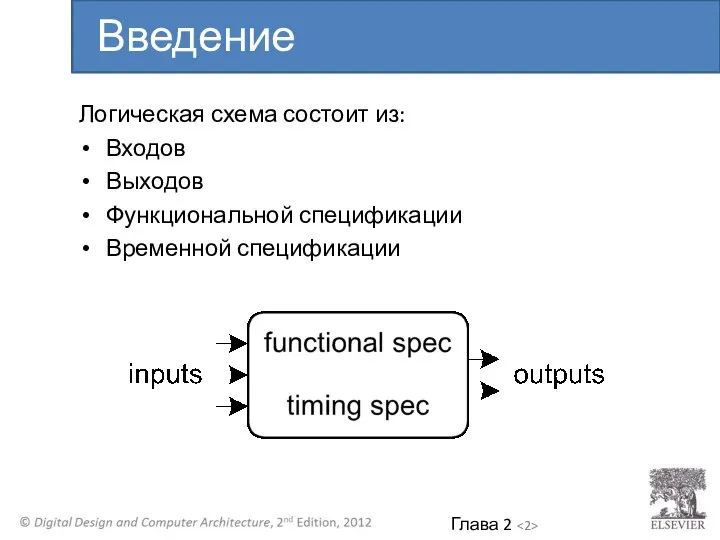
- 2. Логическая схема состоит из: Входов Выходов Функциональной спецификации Временной спецификации Введение
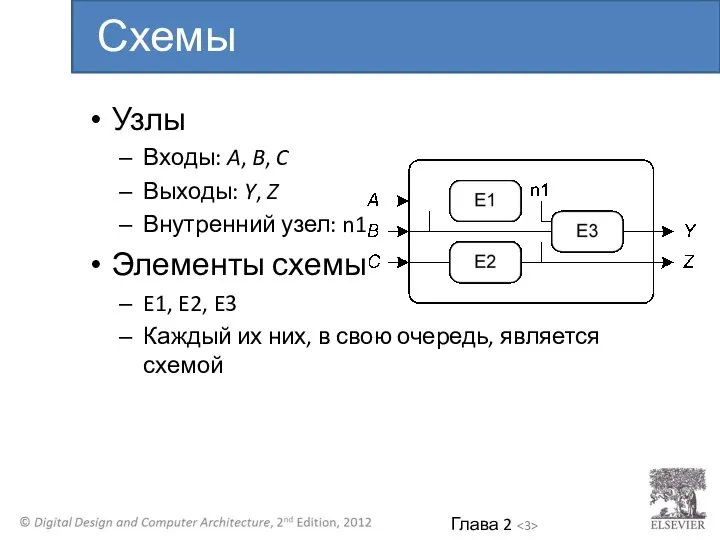
- 3. Узлы Входы: A, B, C Выходы: Y, Z Внутренний узел: n1 Элементы схемы E1, E2, E3
- 4. Комбинационные цифровые схемы Не имеют памяти Выход определяется текущим состоянием входов Последовательностные цифровые схемы Имеют память
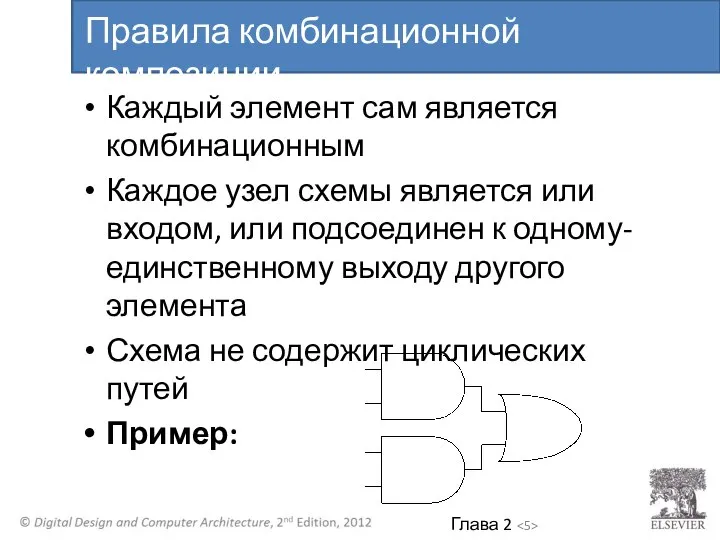
- 5. Каждый элемент сам является комбинационным Каждое узел схемы является или входом, или подсоединен к одному-единственному выходу
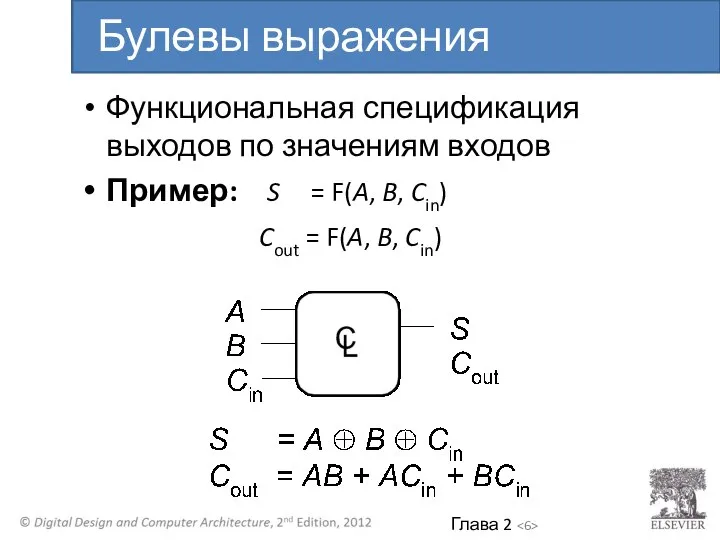
- 6. Функциональная спецификация выходов по значениям входов Пример: S = F(A, B, Cin) Cout = F(A, B,
- 7. Дополнение: переменная с чертой над именем A, B, C Литерал: переменная или ее дополнение A, A,
- 8. Y = F(A, B) = Все выражения могут быть записаны в дизъюнктивной форме Каждой строке соответствует
- 9. Y = F(A, B) = Дизъюнктивная форма Все выражения могут быть записаны в дизъюнктивной форме Каждой
- 10. Y = F(A, B) = AB + AB = Σ(1, 3) Дизъюнктивная форма Все выражения могут
- 11. Y = F(A, B) = (A + B)(A + B) = Π(0, 2) Все булевы выражения
- 12. Вы собираетесь в кафетерий пообедать Вы не пообедаете (E) Там закрыто (не открыто, O) или Они
- 13. Вы собираетесь в кафетерий пообедать Вы не пообедаете (E) Там закрыто (не открыто, O) или Они
- 14. Дизъюнктивная форма (SOP, sum-of-products) сумма (ИЛИ) произведений (И) Конъюнктивная форма (POS, product-of-sums) - произведение (И) сумм
- 15. Дизъюнктивная форма (SOP, sum-of-products) сумма (ИЛИ) произведений (И) Конъюнктивная форма (POS, product-of-sums) - произведение (И) сумм
- 16. Аксиомы и теоремы позволяют упрощать булевы выражения Подобно обычной алгебре, но проще: переменные принимают только два
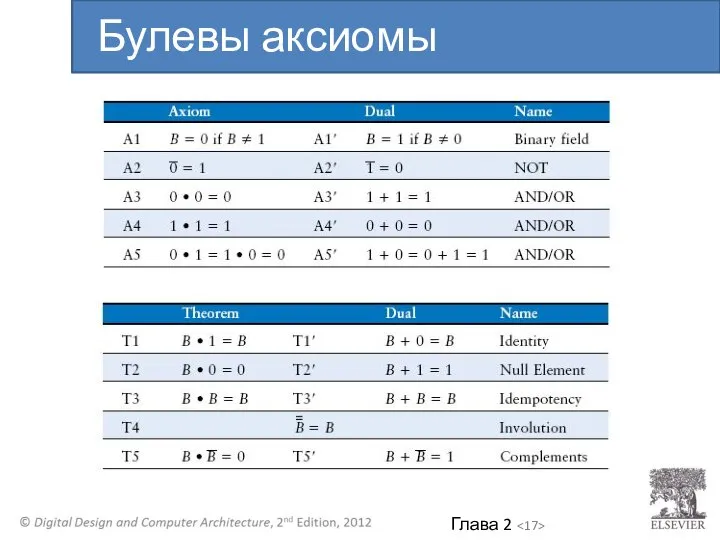
- 17. Булевы аксиомы
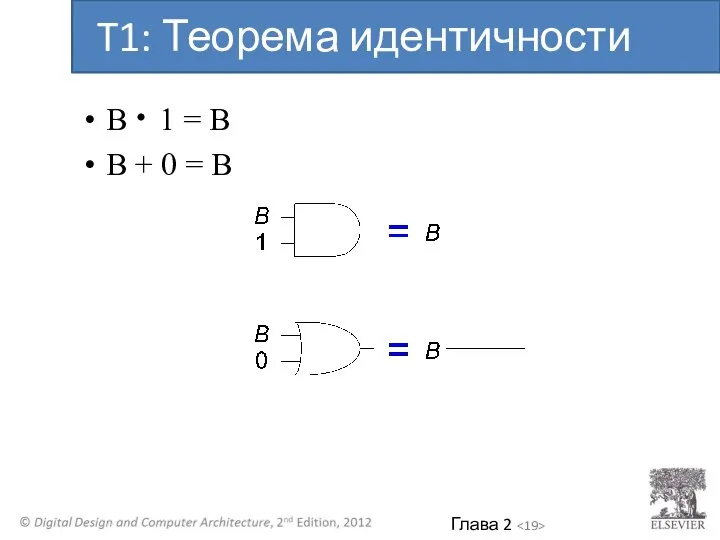
- 18. B 1 = B B + 0 = B T1: Теорема идентичности
- 19. B 1 = B B + 0 = B T1: Теорема идентичности
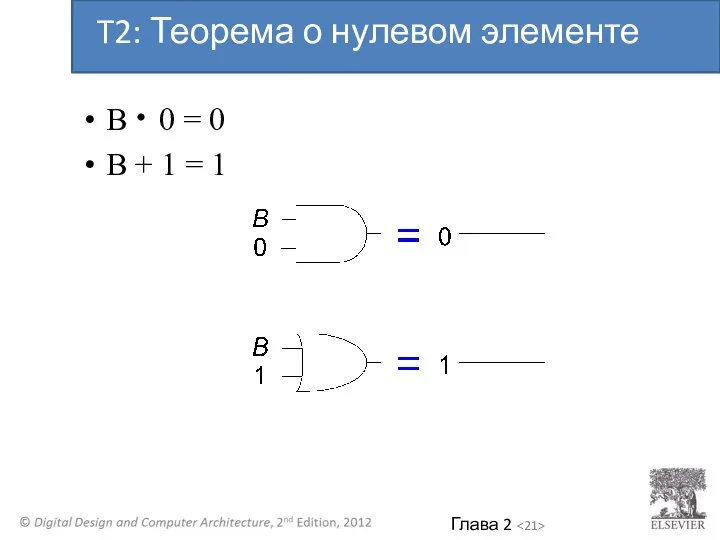
- 20. B 0 = 0 B + 1 = 1 T2: Теорема о нулевом элементе
- 21. B 0 = 0 B + 1 = 1 T2: Теорема о нулевом элементе
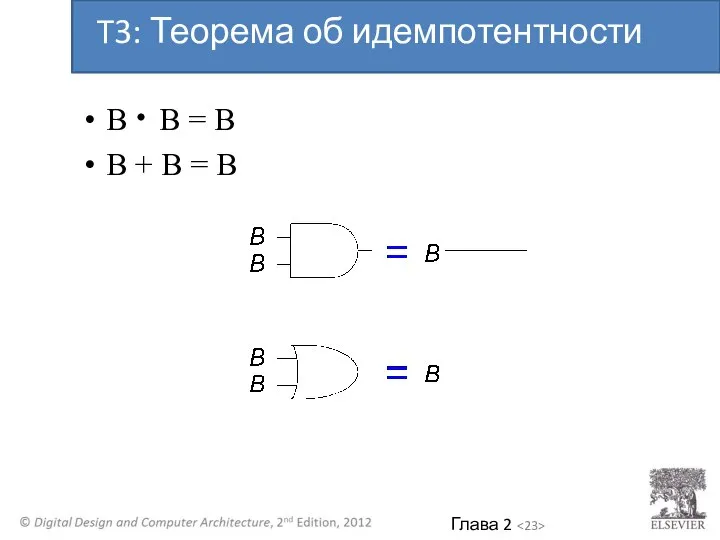
- 22. B B = B B + B = B T3: Теорема об идемпотентности
- 23. B B = B B + B = B T3: Теорема об идемпотентности
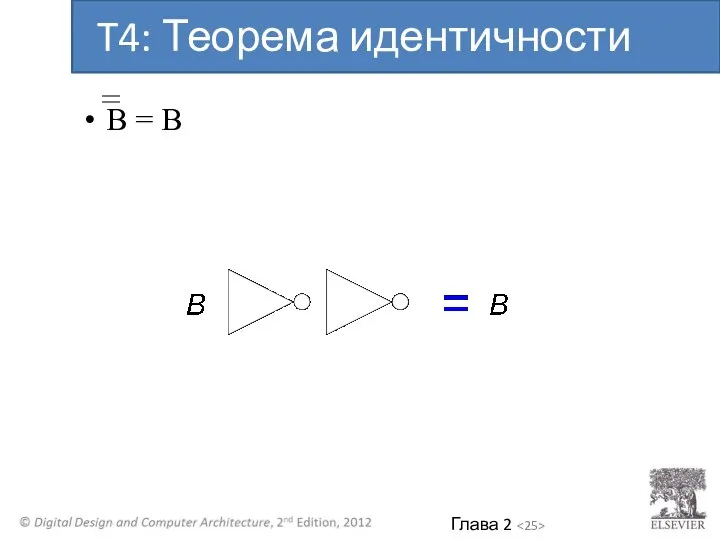
- 24. B = B T4: Теорема идентичности
- 25. B = B T4: Теорема идентичности
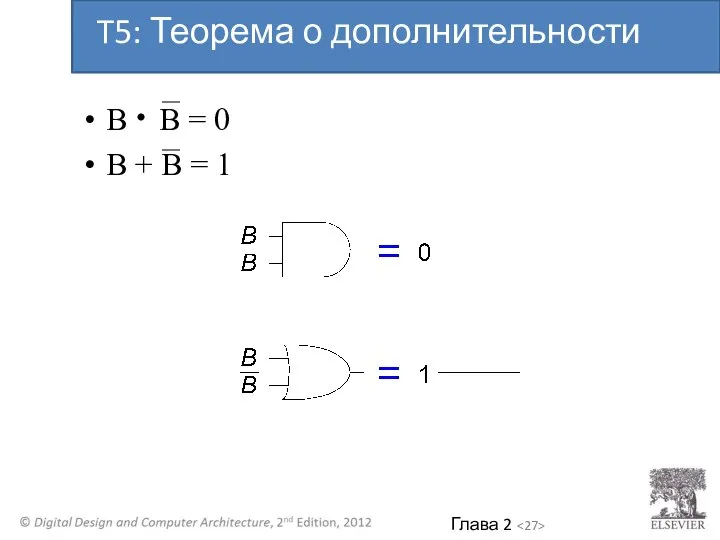
- 26. B B = 0 B + B = 1 T5: Теорема о дополнительности
- 27. B B = 0 B + B = 1 T5: Теорема о дополнительности
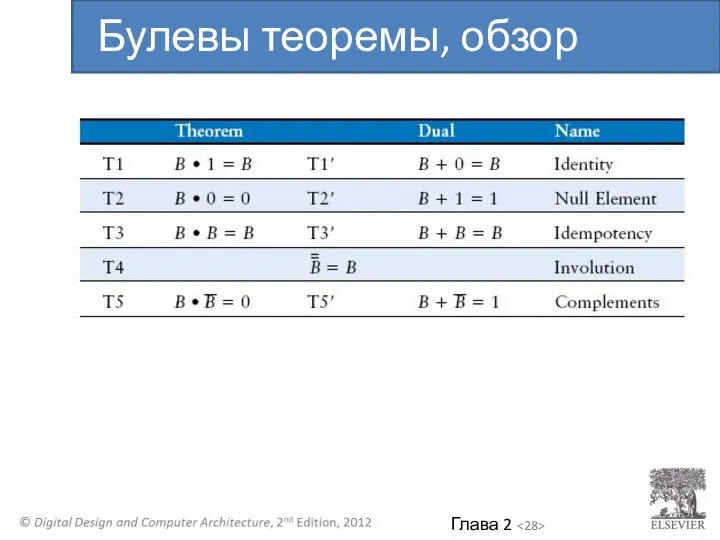
- 28. Булевы теоремы, обзор
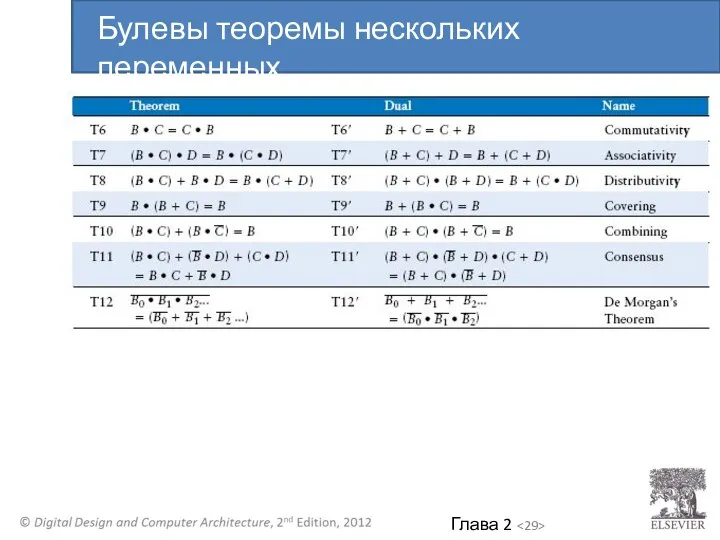
- 29. Булевы теоремы нескольких переменных
- 30. Y = AB + AB Упрощение булевых выражений Пример 1:
- 31. Y = AB + AB = B(A + A) T8 = B(1) T5’ = B T1
- 32. Y = A(AB + ABC) Пример 2: Упрощение булевых выражений
- 33. Y = A(AB + ABC) = A(AB(1 + C)) T8 = A(AB(1)) T2’ = A(AB) T1
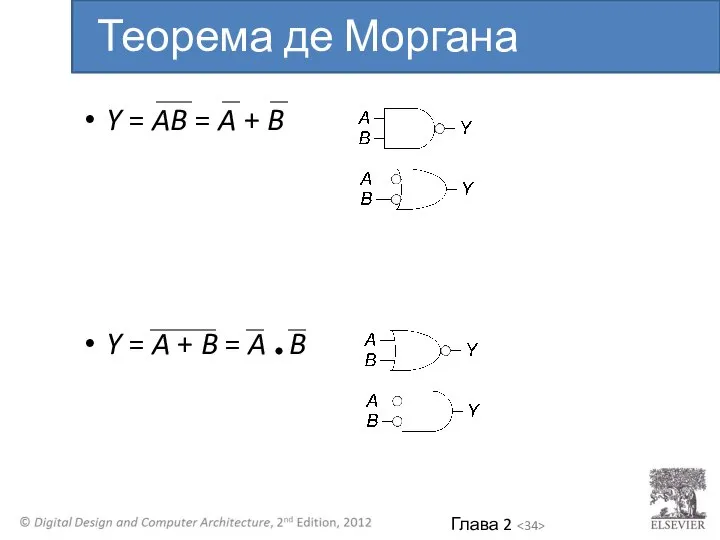
- 34. Y = AB = A + B Y = A + B = A B Теорема
- 35. Назад: Изменить тип элемента Добавить инверсию на входы Вперед: Изменить тип элемента Добавить инверсию на выход
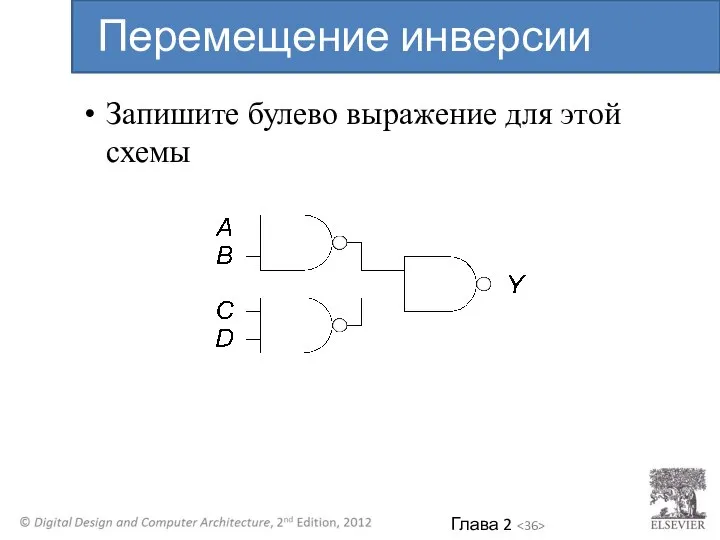
- 36. Запишите булево выражение для этой схемы Перемещение инверсии
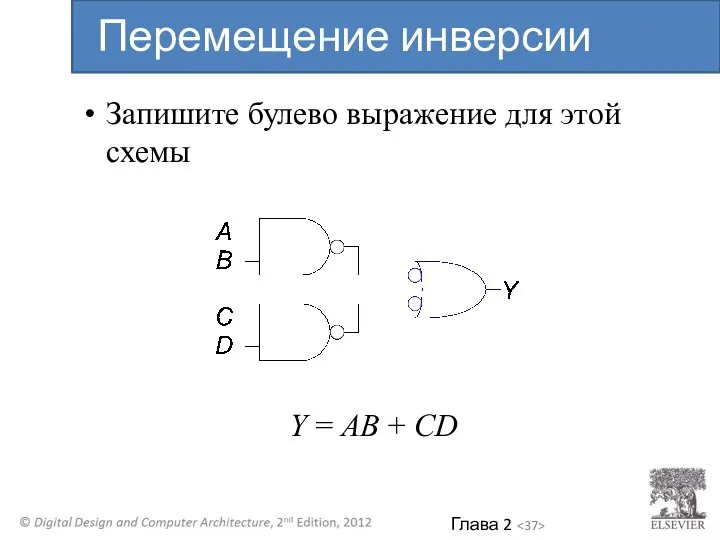
- 37. Запишите булево выражение для этой схемы Y = AB + CD Перемещение инверсии
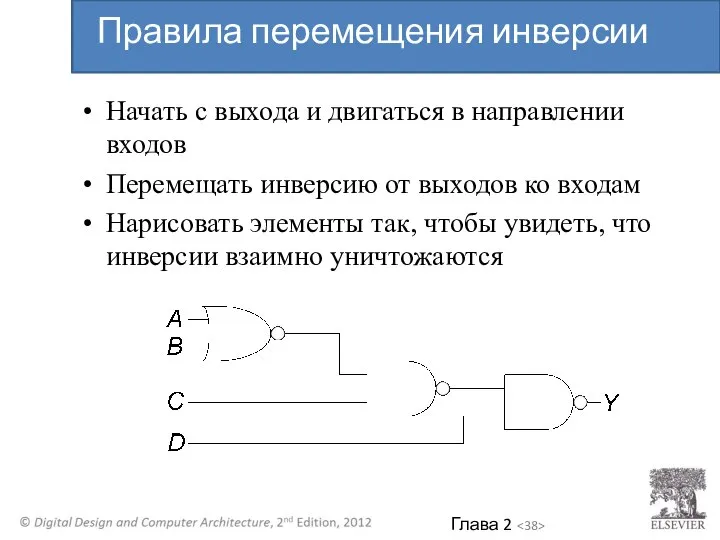
- 38. Начать с выхода и двигаться в направлении входов Перемещать инверсию от выходов ко входам Нарисовать элементы
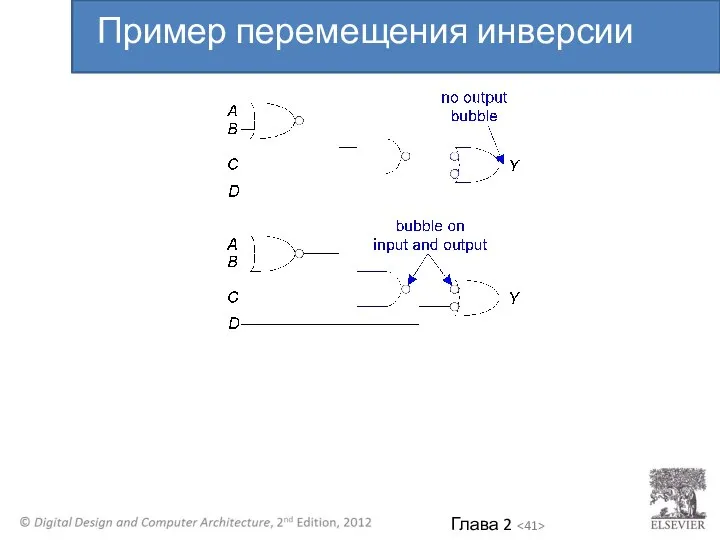
- 39. Пример перемещения инверсии
- 40. Пример перемещения инверсии
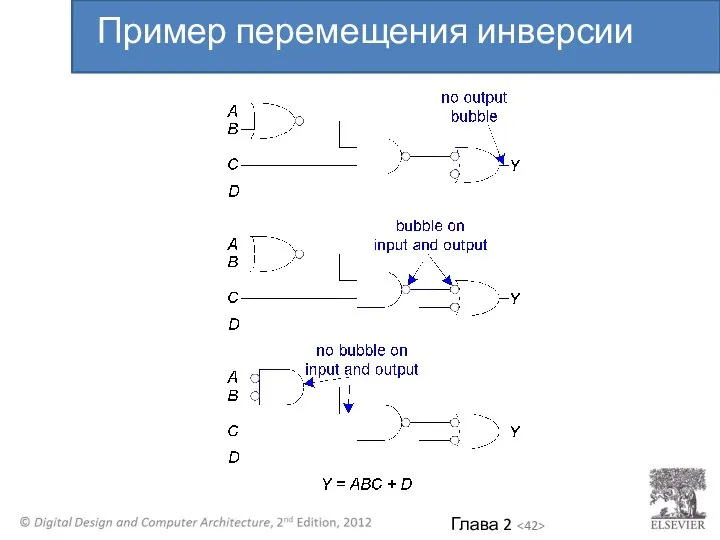
- 41. Пример перемещения инверсии
- 42. Пример перемещения инверсии
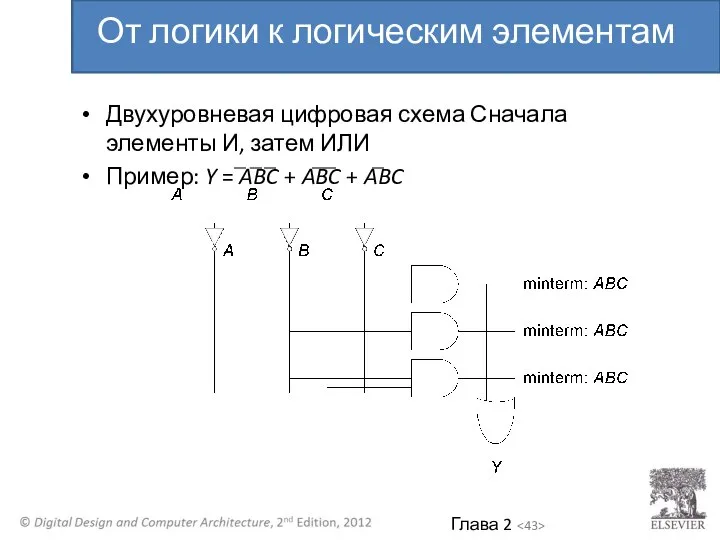
- 43. Двухуровневая цифровая схема Сначала элементы И, затем ИЛИ Пример: Y = ABC + ABC + ABC
- 44. Входы слева (или сверху) Выходы справа (или внизу) Информация передается от элементов, расположенных слева, к элементам,
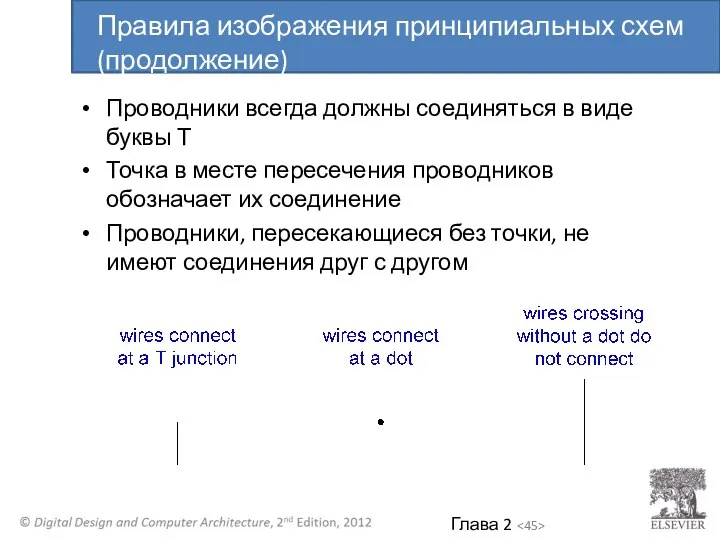
- 45. Проводники всегда должны соединяться в виде буквы Т Точка в месте пересечения проводников обозначает их соединение
- 46. Пример: Схема приоритета Выход устанавливается в соответствии со старшим разрядом который равен ИСТИНЕ Схемы с несколькими
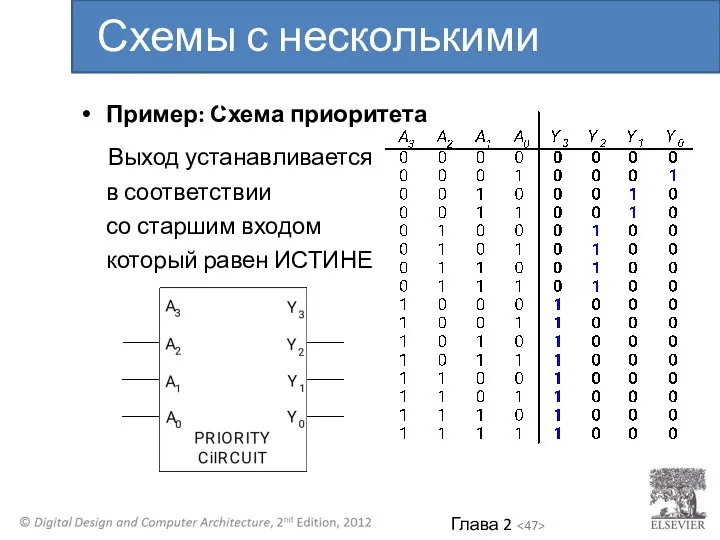
- 47. Пример: Схема приоритета Выход устанавливается в соответствии со старшим входом который равен ИСТИНЕ Схемы с несколькими
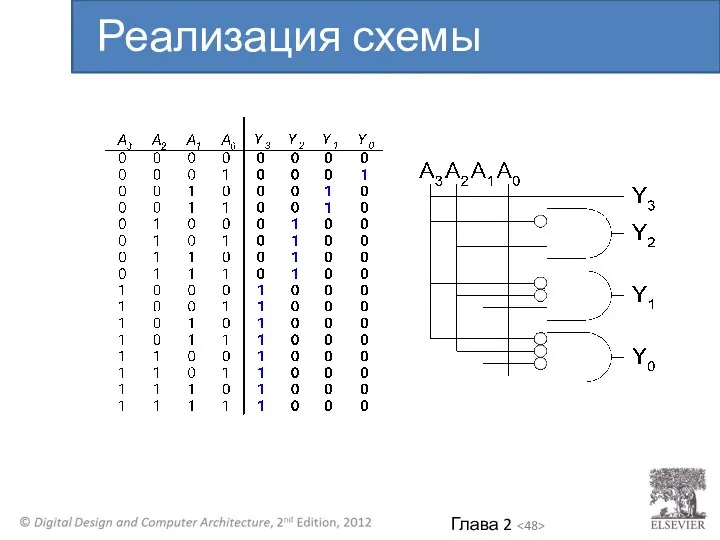
- 48. Реализация схемы приоритета
- 49. Безразличное значение
- 50. Конфликтом: схема пытается установить на выходе одновременно 0 и 1 Действительное значение находится где-то между Может
- 51. Третье состояние, состояние высокого импеданса, неподключенная или плавающая цепь Состояние неподключенного выхода может быть 0, 1
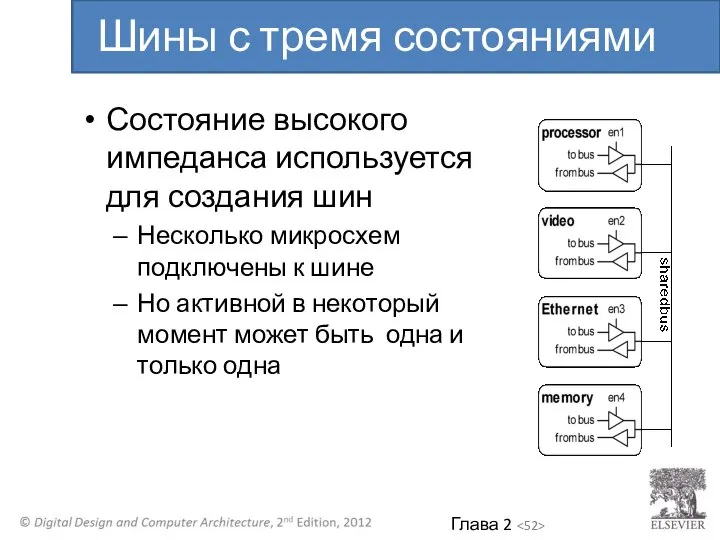
- 52. Состояние высокого импеданса используется для создания шин Несколько микросхем подключены к шине Но активной в некоторый
- 53. Булевы выражения можно упростить путем комбинирования термов Карты Карно позволяют наглядно минимизировать выражение PA + PA
- 54. Обведите овалом 1 в соседних квадратах В булево выражение включаются только те литералы, прямая и инверсная
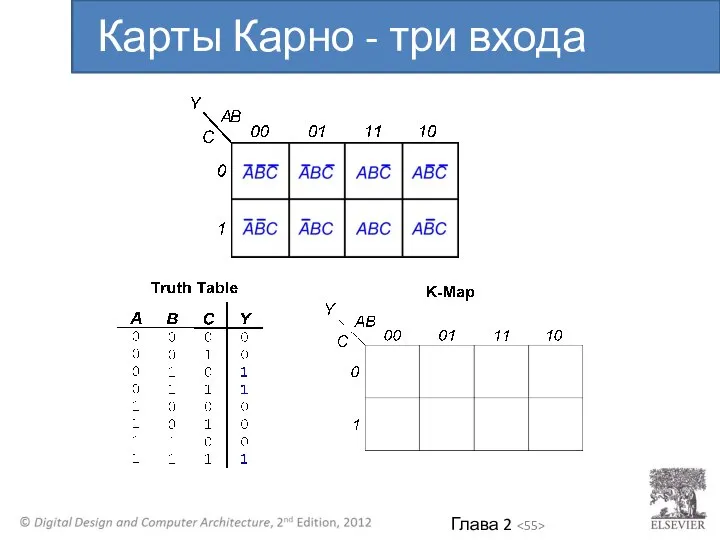
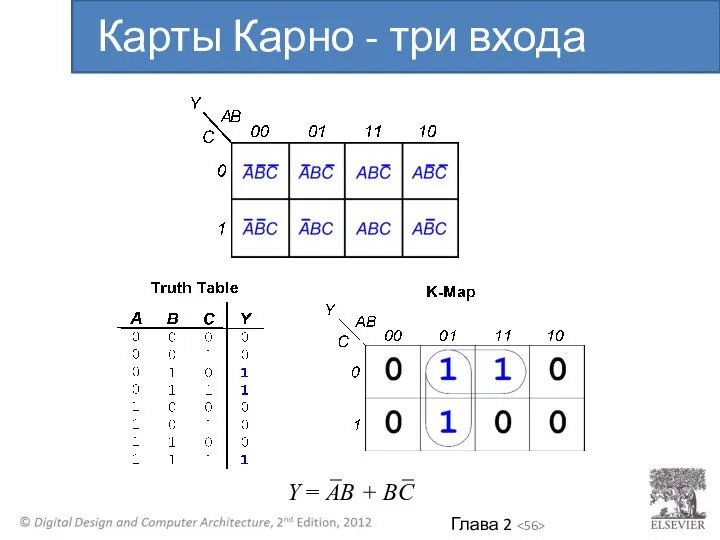
- 55. Карты Карно - три входа
- 56. Y = AB + BC Карты Карно - три входа
- 57. Дополнение: переменная с чертой над именем A, B, C Литерал: Литерал: переменная или ее дополнение A,
- 58. Каждая 1 должна входить хотя бы в один овал Каждый овал должен охватывать блок, число клеток
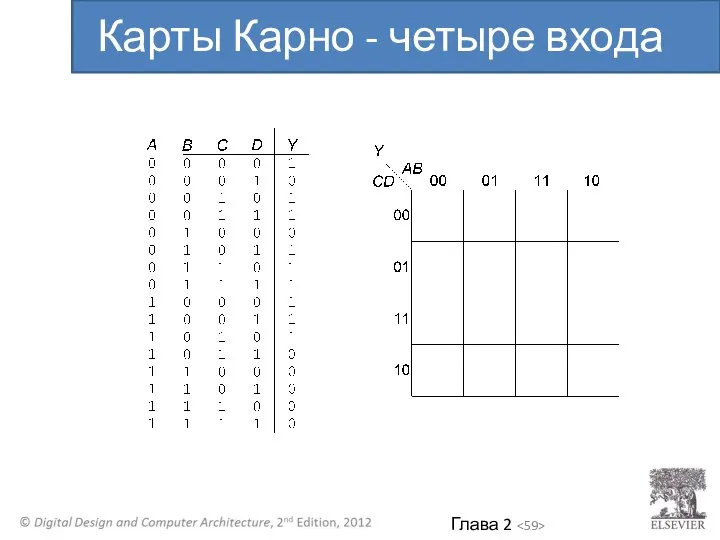
- 59. Карты Карно - четыре входа
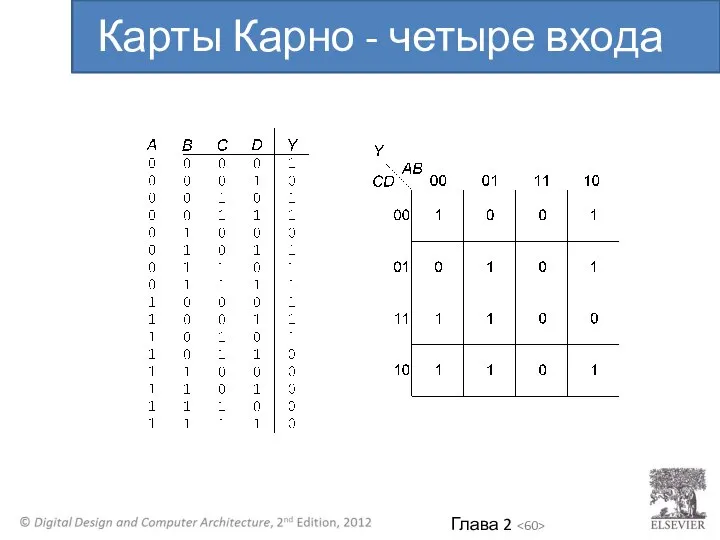
- 60. Карты Карно - четыре входа
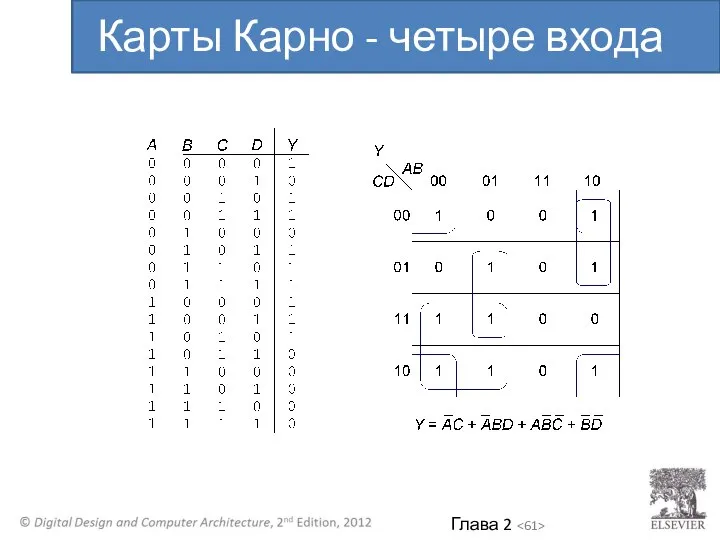
- 61. Карты Карно - четыре входа
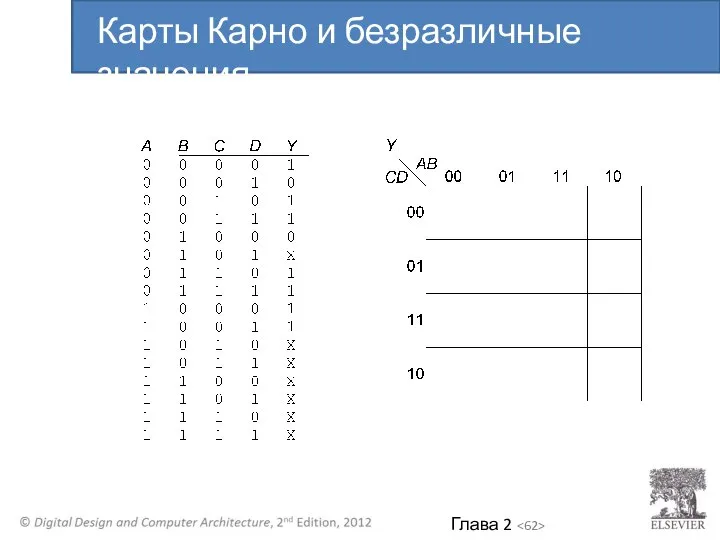
- 62. Карты Карно и безразличные значения
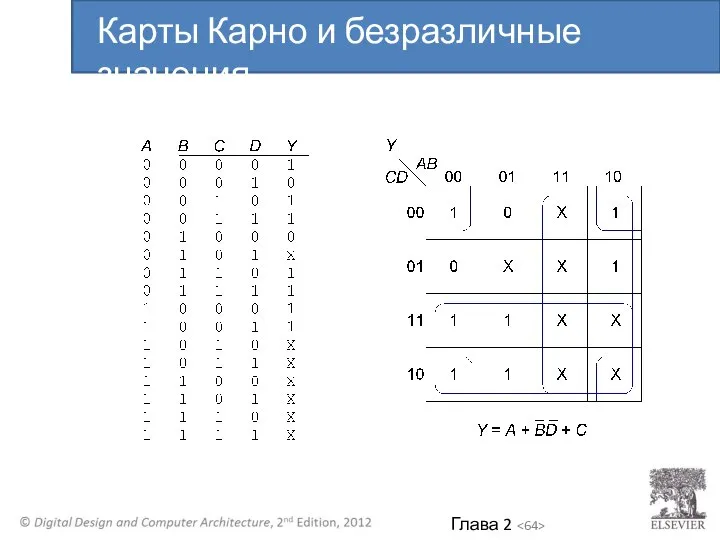
- 63. Карты Карно и безразличные значения
- 64. Карты Карно и безразличные значения
- 65. Мультиплексоры Дешифраторы Базовые комбинационные блоки
- 66. Выбирает один из N входов и соединяет его с выходом log2N-бит для выбора входа – вход
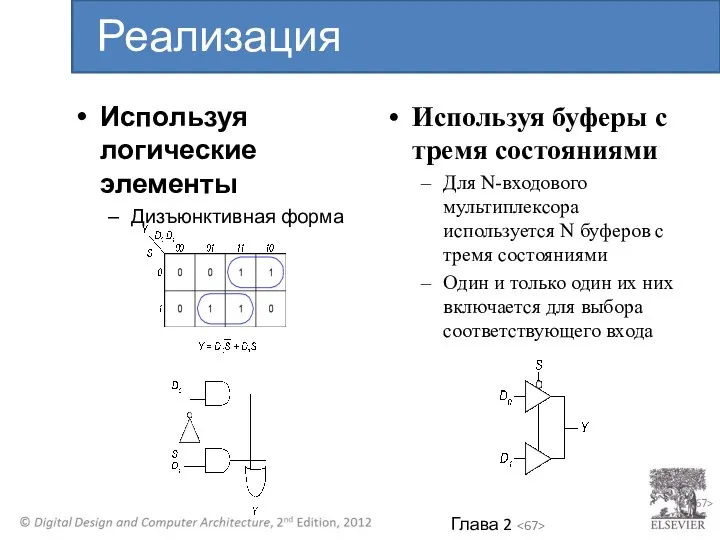
- 67. 2- Используя логические элементы Дизъюнктивная форма Используя буферы с тремя состояниями Для N-входового мультиплексора используется N
- 68. Использование мультиплексоров как таблиц преобразования Цифровые схемы на основе мультиплексоров
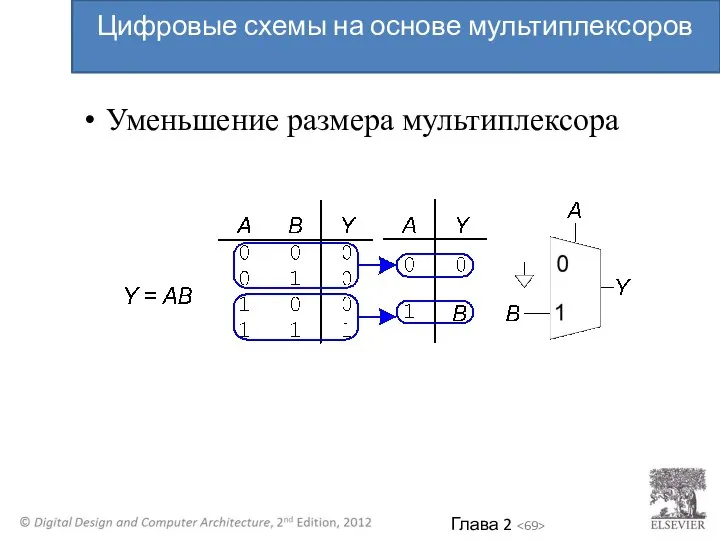
- 69. Уменьшение размера мультиплексора Цифровые схемы на основе мультиплексоров
- 70. N входов, 2N выходов Прямой унитарный код: только один выход принимает значение ИСТИНА Дешифраторы
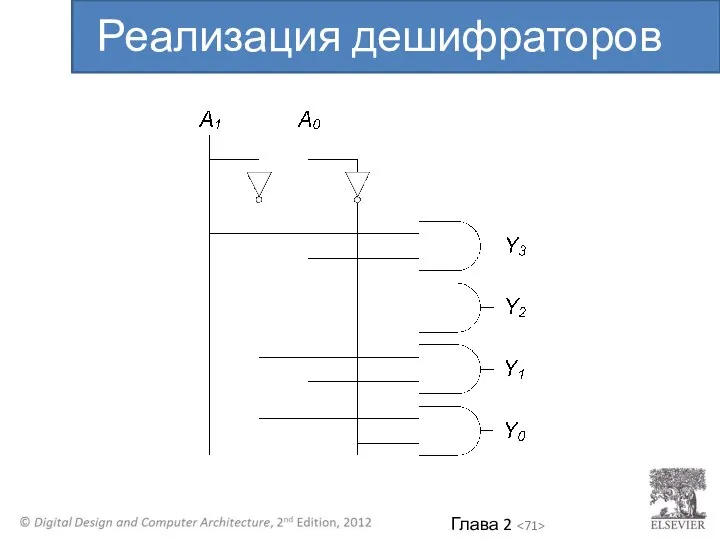
- 71. Реализация дешифраторов
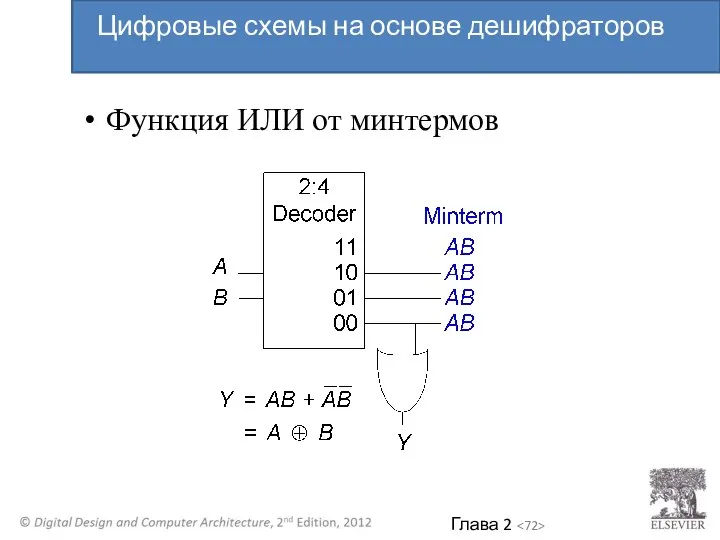
- 72. Функция ИЛИ от минтермов Цифровые схемы на основе дешифраторов
- 73. Задержка между изменением входа и соответствующим изменением выхода Как проектировать быстрые схемы? Временные характеристик
- 74. Задержка распространения tpd = максимальная задержка тракта вход-выход Задержка реакции tcd = минимальная задержка тракта вход-выход
- 75. Задержки обусловлены Емкостями и сопротивлениями в цепях Конечностью скорости света Причины, по которым tpd и tcd
- 76. Критический (длинный) путь tpd = 2tpd_AND + tpd_OR Кратчайший путь tcd = tcd_AND Критический (длинный) и
- 77. Одиночное изменение на входного сигнала вызывает несколько изменений сигнала на выходе Импульсные помехи
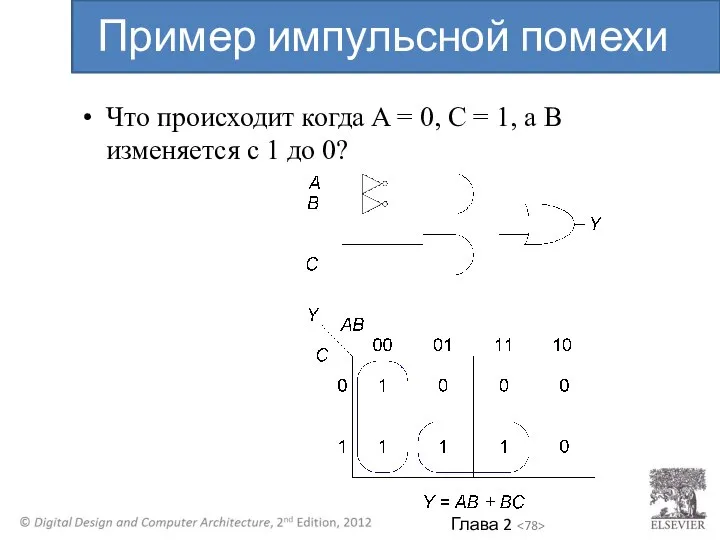
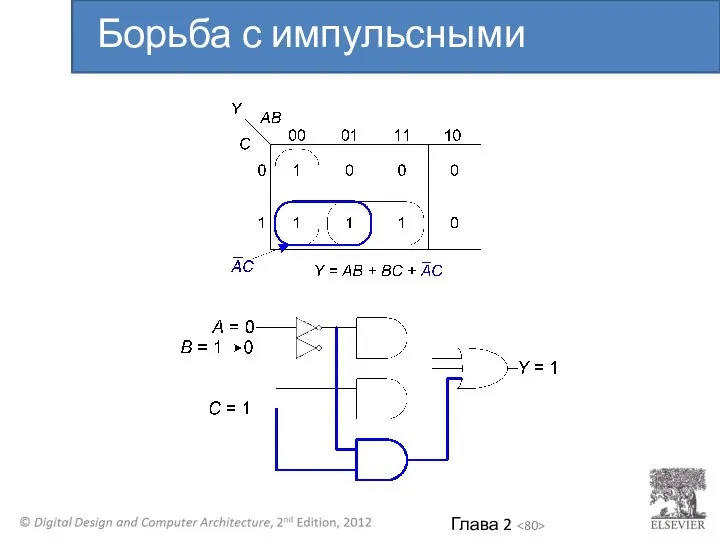
- 78. Что происходит когда A = 0, C = 1, а B изменяется с 1 до 0?
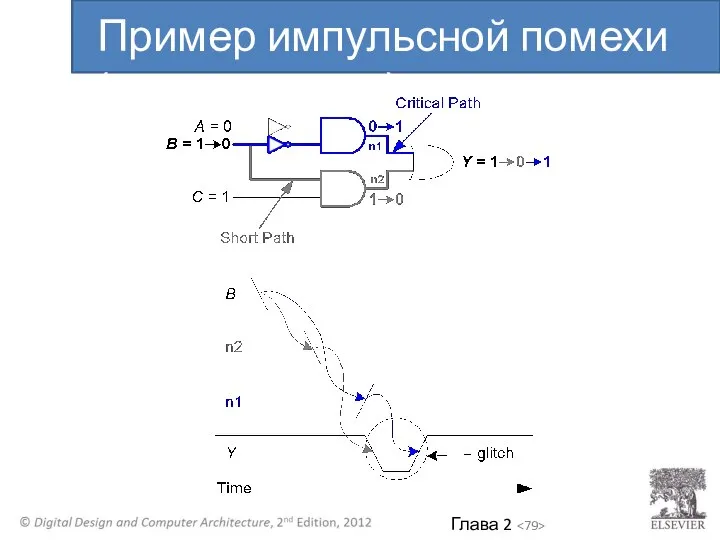
- 79. Пример импульсной помехи (продолжение)
- 80. Борьба с импульсными помехами
- 82. Скачать презентацию










































 омпьютерные методы исследования динамики ЛА
омпьютерные методы исследования динамики ЛА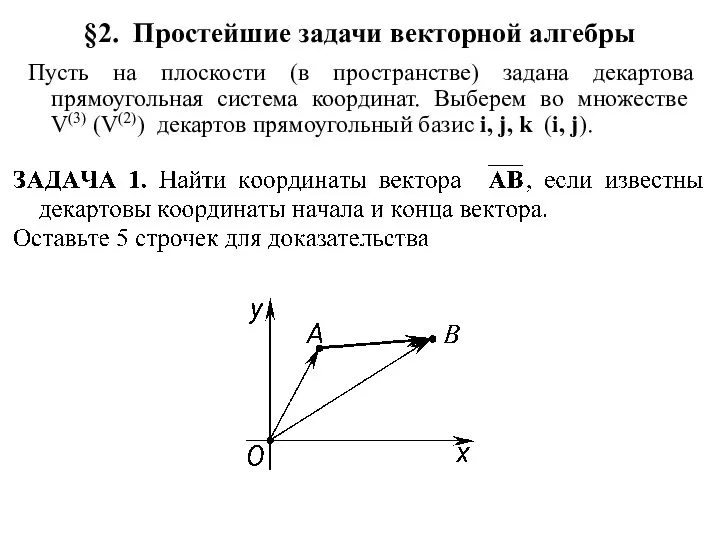 Простейшие задачи векторной алгебры
Простейшие задачи векторной алгебры Преобразование выражения A sin x + B cos х к виду С sin(x+t)
Преобразование выражения A sin x + B cos х к виду С sin(x+t) Параллельность плоскостей
Параллельность плоскостей Основы теории вероятности. Основные понятия и определения
Основы теории вероятности. Основные понятия и определения Логарифмы
Логарифмы Презентация на тему Число и цифра 7 (1 класс)
Презентация на тему Число и цифра 7 (1 класс)  Презентация на тему Табличное решение логических задач (7 класс)
Презентация на тему Табличное решение логических задач (7 класс)  Векторы в пространстве. Практическая работа
Векторы в пространстве. Практическая работа Перпендикулярность плоскостей
Перпендикулярность плоскостей Статистика. Статистические дисциплины
Статистика. Статистические дисциплины Устный счёт. 1 класс
Устный счёт. 1 класс Цилиндр
Цилиндр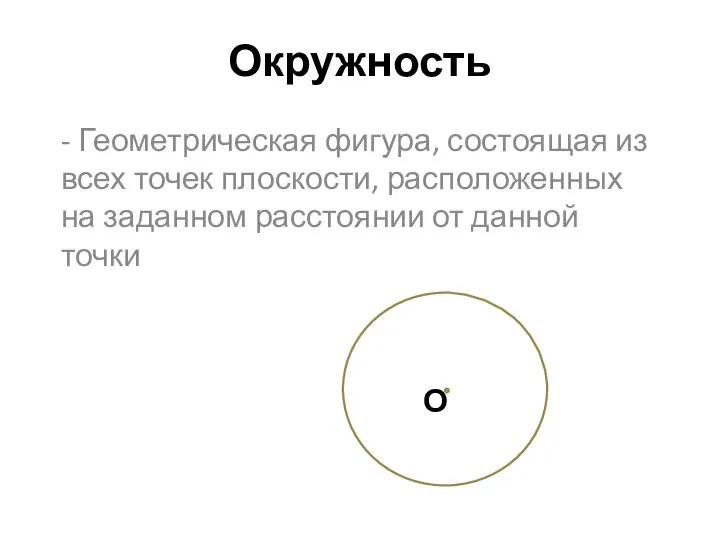 Окружность. Элементы окружности
Окружность. Элементы окружности Задача о Покупке фруктов
Задача о Покупке фруктов Правильные многогранники
Правильные многогранники ОГЭ 2022 Математика. Вариант 14
ОГЭ 2022 Математика. Вариант 14 Признаки параллельности прямых
Признаки параллельности прямых Задачи, обратные данной
Задачи, обратные данной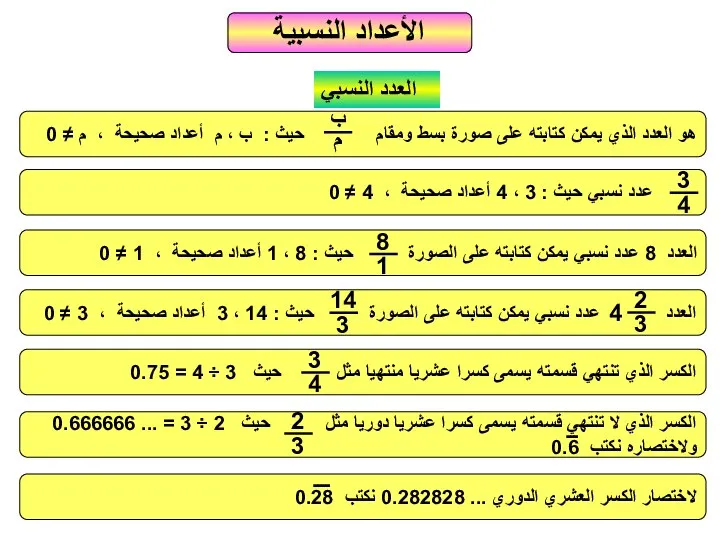 األعداد النسبية العدد النسبي ب
األعداد النسبية العدد النسبي ب Способ вычисления двойных интегралов путем сведения их к повторному интегралу
Способ вычисления двойных интегралов путем сведения их к повторному интегралу Геометрия в учебе и повседневной жизни
Геометрия в учебе и повседневной жизни Способ группировки
Способ группировки Коэффициент корреляции
Коэффициент корреляции Задачи на признаки равенство прямоугольных треугольников
Задачи на признаки равенство прямоугольных треугольников Последние цифры степеней
Последние цифры степеней Отрезок. Длина отрезка
Отрезок. Длина отрезка Геометрия египетских пирамид
Геометрия египетских пирамид