Слайд 2Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство

Слайд 3Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
Рассмотрим функцию y=f(x),

заданную на интервале [a;b].
Разделим интервал [a;b] на n равных частей.
Занумеруем полученные точки xi начиная с нулевого номера
a=xoДлину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].
Слайд 4Численное дифференцирование
Рассмотрим функцию y=f(x).
По определению производной
Из определения предела получаем
приближенное равенство
Рассмотрим функцию y=f(x),

заданную на интервале [a;b].
Разделим интервал [a;b] на n равных частей.
Занумеруем полученные точки xi начиная с нулевого номера a=xoДлину каждого интервала будем называть шагом h=(b-a)/n,
а полученные точки {xi } и шаг h разбиением интервала [a;b].
В каждой точке xi вычислим значение функции yi =f(xi ).
Полученную пару (xi ; yi ) будем называть узлами функции.
Слайд 6
Однако если возьмем Δx = – h, тогда получим
Или .
(2)

Слайд 7
Аналогично взяв Δx = 2h, получим
или
(3)

Слайд 8
Аналогично взяв Δx = 2h, получим
или
(3)
Полученные формулы (1) – (3)

называются соответственно правой, левой и центральной разностными формулами численного дифференцирования для первой производной.
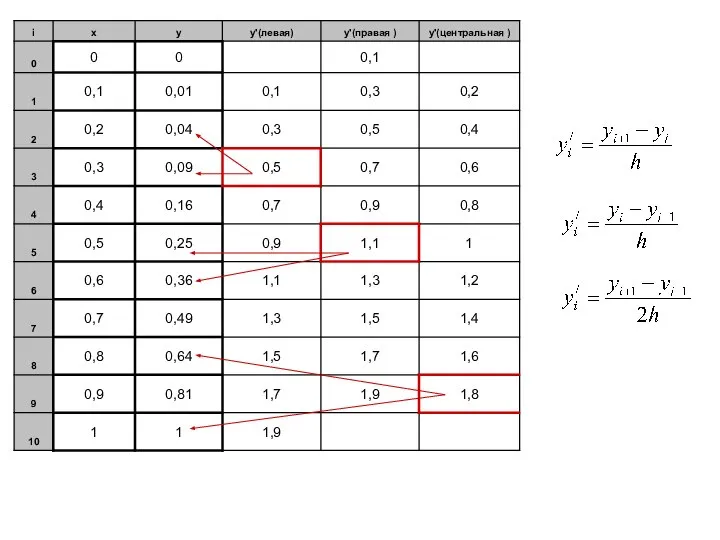
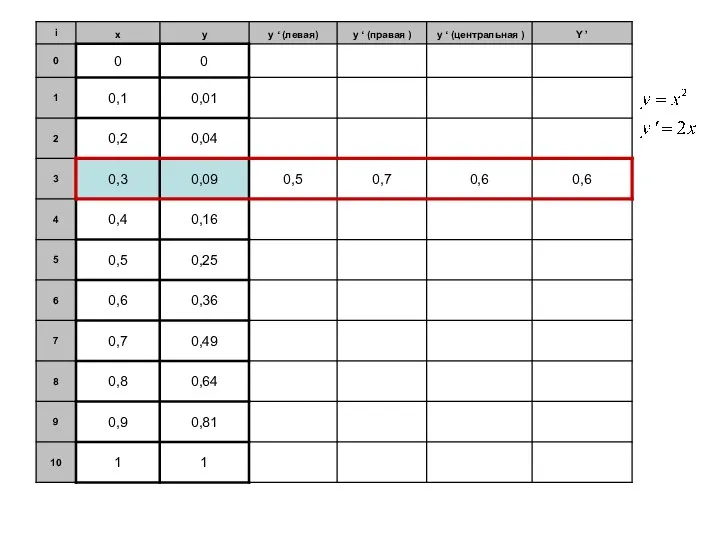
Слайд 9Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с шагом 0,1.
Найдем
![Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с шагом 0,1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1024027/slide-8.jpg)
первую производную этой функции.
Мы вывели для этого три различные формулы (1), (2) и (3).
Слайд 12
Аналогично определяются разностные формулы и для старших производных.
Или

Слайд 15
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем говорить, что

функция задана неравномерной сеткой,
если hi =xi +1 – xi =/= hj=x j+1 – xj
Слайд 16
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем говорить, что

функция задана неравномерной сеткой,
если hi =xi +1 – xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
Слайд 17
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем говорить, что

функция задана неравномерной сеткой,
если hi =xi +1 – xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
Слайд 18
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем говорить, что

функция задана неравномерной сеткой,
если hi =xi +1 – xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
Слайд 19
Неравномерная сетка
Рассмотрим функцию y=f(x), заданную узлами Mi=(xi ; yi )
Будем говорить, что

функция задана неравномерной сеткой,
если hi =xi +1 – xi =/= hj=x j+1 – xj
Тогда - правая производная, где hi-1=x i+1 –xi
левая производная,
где hi-1=xi –x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
Слайд 20
- правая производная,
где hi-1=x i+1 –xi
левая производная,
где hi-1=xi

–x i-1
центральная производная,
где hi + hi-1 =x i+1 – x i-1
Общая формула
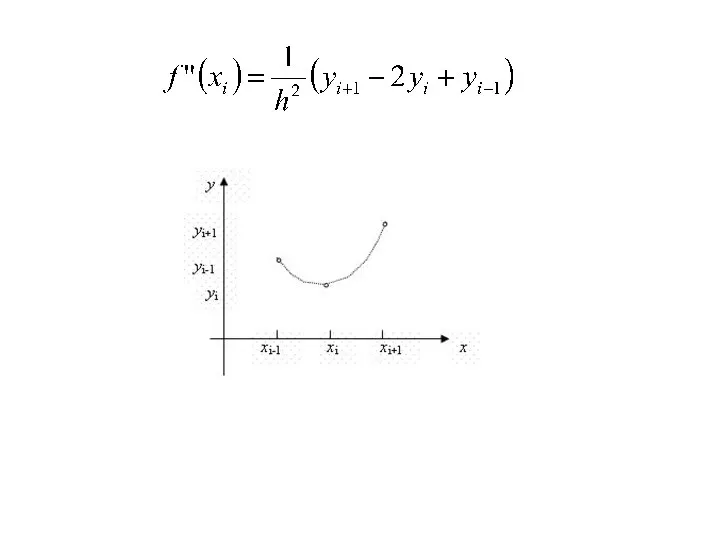
Слайд 21Вторая производная задается формулой

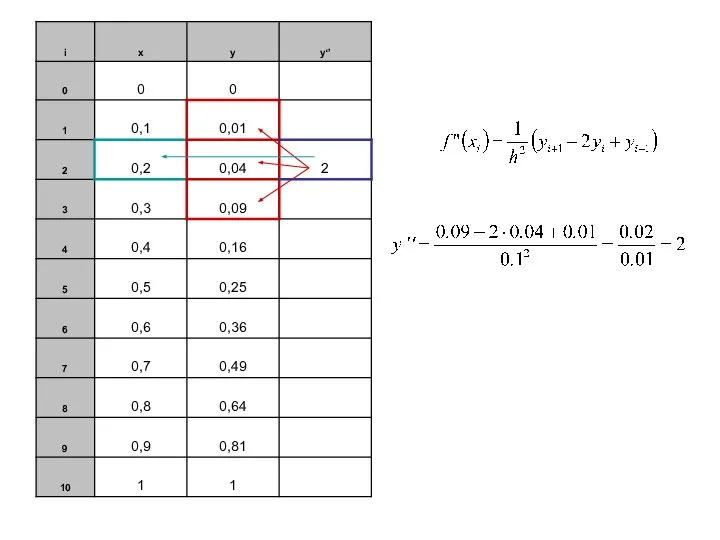
Слайд 22Пример.
Рассмотрим функцию, заданную таблицей
Найти Y/(0.2) и Y//(0.2)
- Правая








![Рассмотрим функцию y=f(x), заданную на интервале [0;1] и протабулированную с шагом 0,1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1024027/slide-8.jpg)









 Презентация на тему Преобразование выражений содержащих квадратные корни
Презентация на тему Преобразование выражений содержащих квадратные корни  Презентация на тему Математика вокруг нас 6 класс для учителя
Презентация на тему Математика вокруг нас 6 класс для учителя  Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Проекция вектора
Проекция вектора Презентация на тему Задачи на приведение к единице (3 класс)
Презентация на тему Задачи на приведение к единице (3 класс)  Логарифмы
Логарифмы Исаак Ньютон
Исаак Ньютон Diskretnaya_matematika-2 2
Diskretnaya_matematika-2 2 Таблица сложения в пределах 20
Таблица сложения в пределах 20 Операции, функции, выражения
Операции, функции, выражения Решение задач с помощью пропорции. 5 класс
Решение задач с помощью пропорции. 5 класс Пропорциональные величины
Пропорциональные величины Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова
Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова Редкозубова О.Ф., учитель математики МОУ «СОШ № 138»
Редкозубова О.Ф., учитель математики МОУ «СОШ № 138» Мастер-класс в рамках игры физико-математические забавы
Мастер-класс в рамках игры физико-математические забавы Признаки равенства треугольников
Признаки равенства треугольников Вавилонская система счисления
Вавилонская система счисления Презентация на тему Векторы
Презентация на тему Векторы  Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Геометрические построения
Геометрические построения Признак параллельности прямых по равенству соответственных углов
Признак параллельности прямых по равенству соответственных углов Уравнение сферы
Уравнение сферы Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Средние величины. (Лекция 4.2)
Средние величины. (Лекция 4.2) Умножение и деление. Урок-путешествие
Умножение и деление. Урок-путешествие Теория в области нечеткой логики и нечеткого множества
Теория в области нечеткой логики и нечеткого множества Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Сериал Законы сложения
Сериал Законы сложения