Выпуклые многогранники

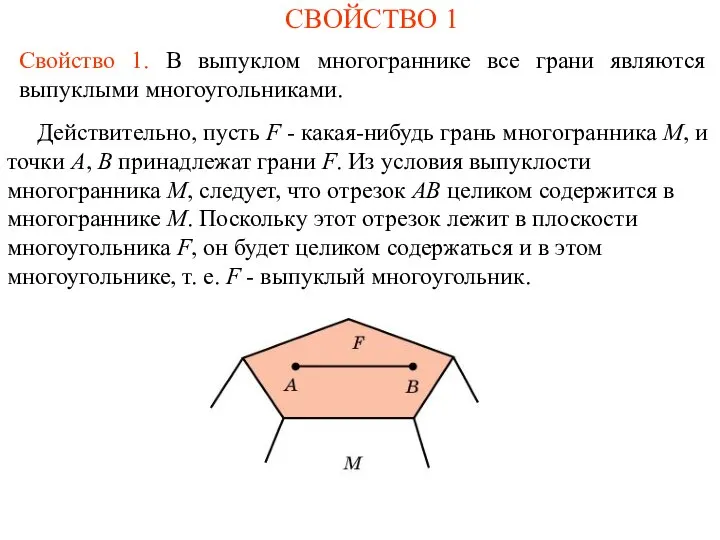
СВОЙСТВО 1
Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Действительно, пусть F - какая-нибудь грань многогранника M, и точки A, B принадлежат грани F. Из условия выпуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т. е. F - выпуклый многоугольник.

СВОЙСТВО 2
Действительно, пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т. е. такую его точку, которая не принадлежит ни одной грани многогранника M. Соединим точку S с вершинами многогранника M отрезками. Заметим, что в силу выпуклости многогранника M, все эти отрезки содержатся в M. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника M. Эти пирамиды целиком содержатся в M, и все вместе составляют многогранник M.
Свойство 2. Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

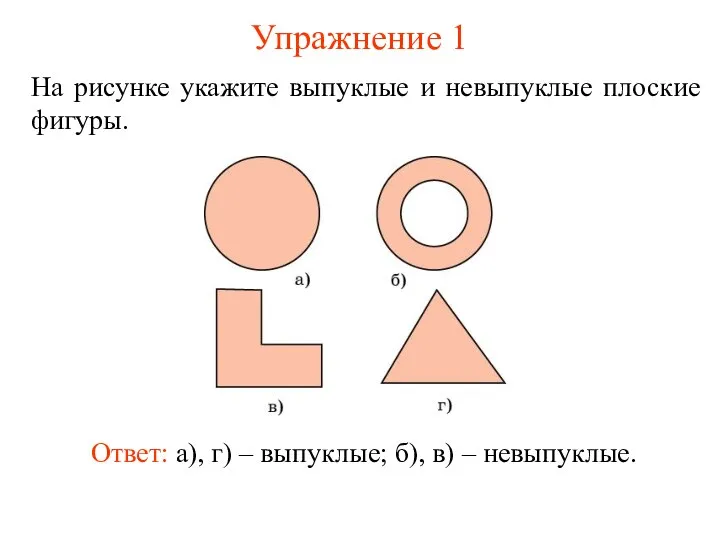
Упражнение 1
На рисунке укажите выпуклые и невыпуклые плоские фигуры.
Ответ: а), г) – выпуклые; б), в) – невыпуклые.

Упражнение 2
Всегда ли пересечение выпуклых фигур является выпуклой фигурой?
Ответ: Да.

Упражнение 3
Всегда ли объединение выпуклых фигур является выпуклой фигурой?
Ответ: Нет.

Упражнение 4
Можно ли составить выпуклый четырёхгранный угол с такими плоскими углами: а) 56о, 98о, 139о и 72о; б) 32о, 49о, 78о и 162о; в) 85о, 112о, 34о и 129о; г) 43о, 84о, 125о и 101о.
Ответ: а) Нет;
б) да;
в) нет;
г) да.

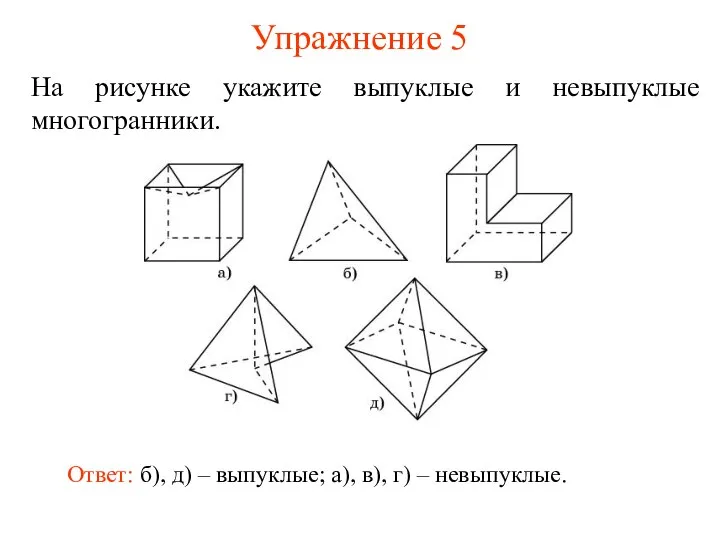
Упражнение 5
На рисунке укажите выпуклые и невыпуклые многогранники.
Ответ: б), д) – выпуклые; а), в), г) – невыпуклые.

Упражнение 6
Может ли невыпуклый многоугольник быть гранью выпуклого многогранника?
Ответ: Нет.

Упражнение 7
Может ли сечением выпуклого многогранника плоскостью быть невыпуклый многоугольник?
Ответ: Нет.

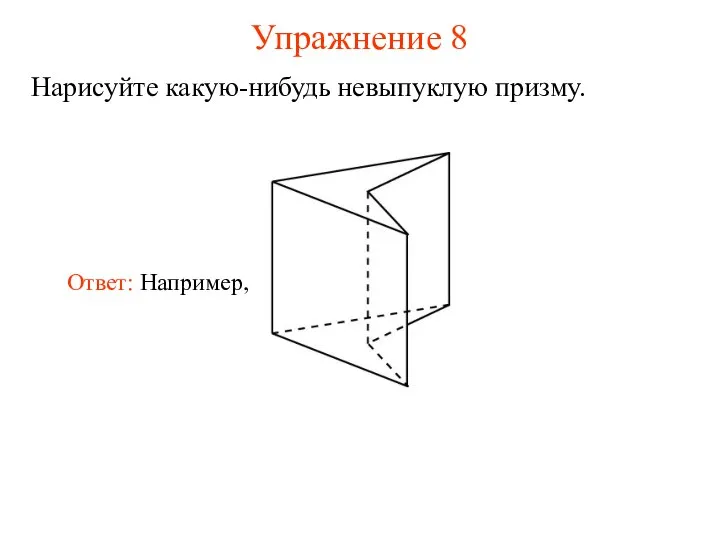
Упражнение 8
Нарисуйте какую-нибудь невыпуклую призму.

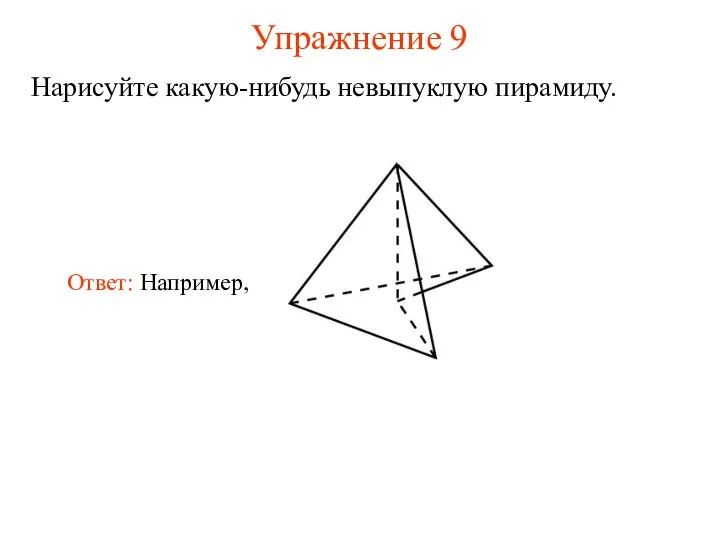
Упражнение 9
Нарисуйте какую-нибудь невыпуклую пирамиду.

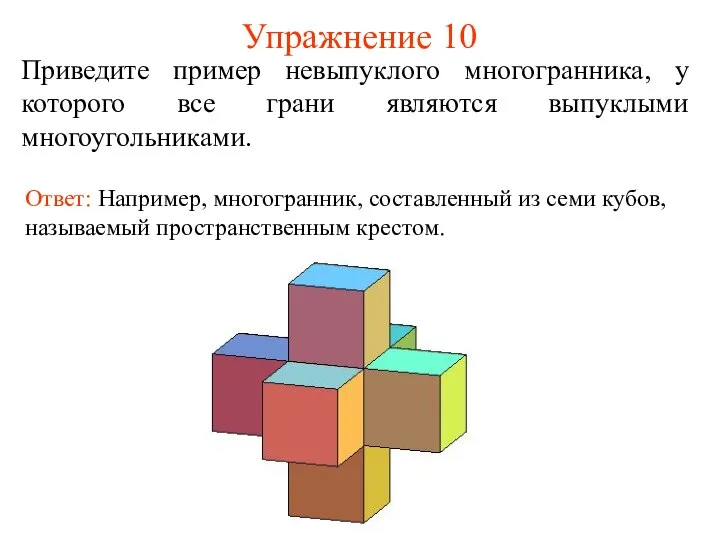
Упражнение 10
Приведите пример невыпуклого многогранника, у которого все грани являются выпуклыми многоугольниками.
Ответ: Например, многогранник, составленный из семи кубов, называемый пространственным крестом.

Упражнение 11*
Докажите, что для любого n > 7 существует многогранник с n ребрами.
Решение. Если n = 2k (k >2), то примером многогранника с n ребрами является k-угольная пирамида.
Если n = 2k +3 (k > 2), то примером многогранника с n ребрами является k-угольная пирамида, у которой отрезан один угол при основании, как это было сделано ранее.

Упражнение 12*
Докажите, что для у любого многогранника найдутся две грани с одинаковым числом ребер. Приведите пример многогранника, у которого нет трех граней с одинаковым числом ребер
Решение. Рассмотрим грань многогранника с наибольшим числом ребер. Обозначим это число ребер n. К этой грани примыкают n граней, числа ребер которых могут быть 3, …, n. Таких чисел n – 2. Следовательно, среди этих n граней найдутся грани, имеющие одинаковое число ребер.

Упражнение 13*
Докажите, что для у любого многогранника найдутся две вершины, в которых сходится одинаковое число ребер. Приведите пример многогранника, у которого нет трех вершин с одинаковым числом ребер
Решение. Рассмотрим вершину многогранника с наибольшим числом ребер. Обозначим это число ребер n. Концами этих ребер являются n вершин, числа ребер которых могут быть 3, …, n. Таких чисел n – 2. Следовательно, среди этих n вершин найдутся вершины, в которых сходится одинаковое число ребер.

Упражнение 14*
Докажите, что для у любого многогранника число граней с нечетным числом ребер четно.
Решение. Предположим, что число граней с нечетным числом ребер нечетно. Тогда общее число ребер в этих гранях будет нечетным. Общее число ребер в гранях с четным числом ребер четно. Поэтому число ребер всех граней будет нечетно. Однако каждое ребро входит ровно в две грани, и при подсчете ребер, входящих в грани, мы считали каждое ребро дважды, т.е. оно должно быть четным. Противоречие. Следовательно, число граней с нечетным числом ребер должно быть четно.