Содержание
- 2. Современная дидактика обращаясь к игровым формам обучения на уроках, справедливо усматривает в них возможности эффективной организации
- 3. Развитие интереса к математике, активности и увлеченности учеников, развитие любознательности, глубокого познавательного интереса. Возможности эффективной организации
- 4. Научить учащихся применять знания в новых условиях или ставить умственную задачу, решение которой требует проявления разнообразных
- 5. Дидактические игры являются одним из эффективных средств активизации познавательной деятельности учащихся, разработанные с учетом возрастных и
- 6. Дидактические игры позволяют проверить умения учащихся выполнять математические действия, анализировать, сравнивать, подмечать закономерности, повысить интерес к
- 7. Наиболее целесообразно использовать дидактические игры при проверке результатов обучения при выработке навыков при формировании умений
- 8. Игры, направленные на формирование и совершенствование навыков устного счета. Игры, направленные на актуализацию теоретических знаний («Поле
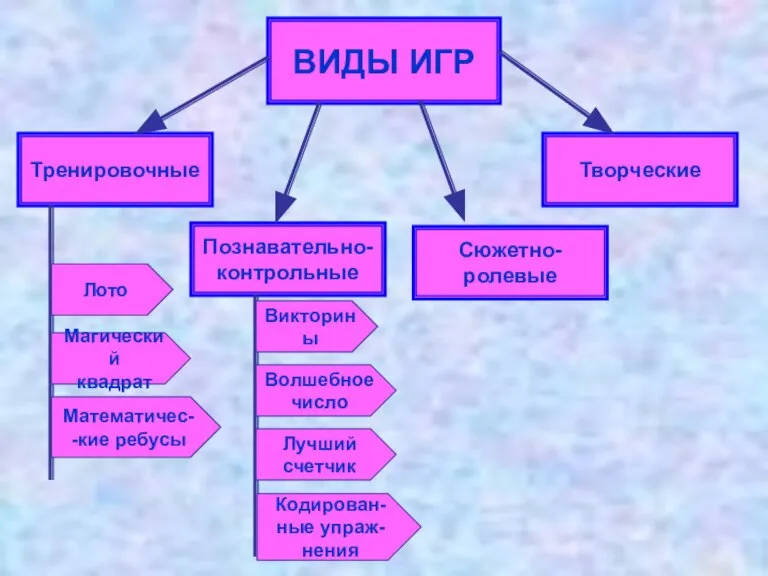
- 9. ВИДЫ ИГР Тренировочные Познавательно- контрольные Сюжетно- ролевые Творческие Лото Математичес- -кие ребусы Магический квадрат Викторины Лучший
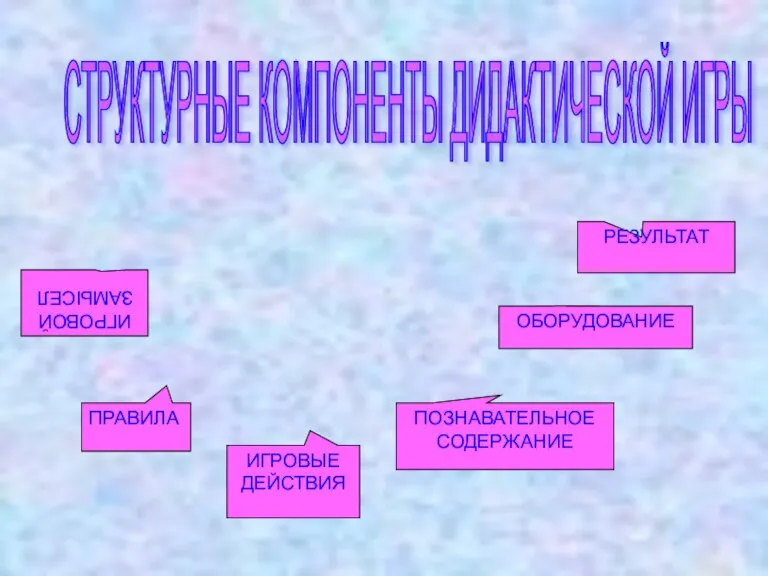
- 10. ИГРОВОЙ ЗАМЫСЕЛ ПРАВИЛА ИГРОВЫЕ ДЕЙСТВИЯ СТРУКТУРНЫЕ КОМПОНЕНТЫ ДИДАКТИЧЕСКОЙ ИГРЫ ПОЗНАВАТЕЛЬНОЕ СОДЕРЖАНИЕ ОБОРУДОВАНИЕ РЕЗУЛЬТАТ
- 11. 1. Правила игры должны быть простыми, точно сформулированными, а математическое содержание предлагаемого материала – доступно пониманию
- 12. Учитель должен определить место дидактических игр в системе других видов деятельности на уроке; определить целесообразность использования
- 13. 5 класс Выберите соответствующую дробь 10% 50% 30% 75% 25% 90% Игра "Светофор" 1/10 5/100 3/100
- 14. 8 класс Выберите соответствующее неравенство или числовой промежуток Вопросы ответы -3x x x>-5 2. 2x>-18 x
- 15. Туристы проехали 50% пути на поезде и 40% пути на автобусе. Весь ли путь они проехали
- 16. Например: 1. -25+8 -17-21 -36*(-2) -5*2,1 2. 48*7/8 48*5/12 48*3/4 48*3/16 48*5/6 3. 71/12 + 1
- 17. Например предлагается определить значение переменных Р в 4 раза меньше 36 С в 2 раза больше
- 18. 325 Увеличить на 10 Округлить до десятков Отнять количество десятков Записать ближайшее следующее число, кратное 4
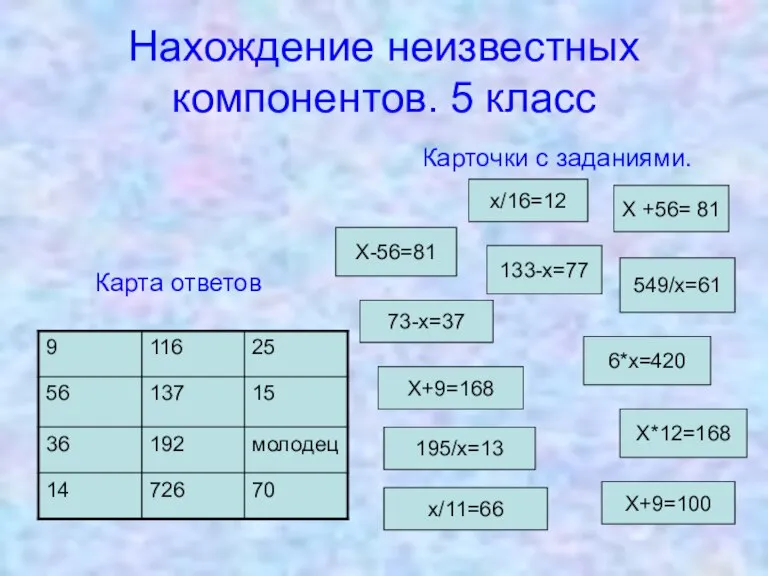
- 19. В этой игре каждый участник получает основную карту с ответами и маленькие карточки с заданиями. Учащийся,
- 20. Нахождение неизвестных компонентов. 5 класс Карточки с заданиями. Х +56= 81 Х*12=168 133-х=77 х/16=12 х/11=66 Х+9=168
- 21. Цель: закрепление умений сравнивать обыкновенные дроби с одинаковыми знаменателями Правила игры: 1. Перемешайте карточки и положите
- 22. Особое место занимают творческие и ролевые игры. Проводятся они один-два раза в год, так как требуют
- 23. Одна из форм дидактических игр – деловая игра. Деловая игра – модель процесса принятия решений в
- 24. Цель: закрепление различных формул. Правила игры. Пасьянс содержит 20 карточек, на которых написано 10 формул (
- 25. ПАСЬЯНС ( пример ). Удачные пары:
- 26. развивают навыки учеников в заданиях на вычисления, при решении уравнений, процентных задач и также текстовых задач,
- 27. Математические викторины - это особый вид игры, которая ставит своей целью выявить учащихся с наибольшим математическим
- 28. Математическими ребусами называют задания на восстановление записей вычислений. Условие математического ребуса содержит либо целиком зашифрованную запись,
- 30. Скачать презентацию
























 Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы 3_TEMA_3_Matematicheskaya_logika_1
3_TEMA_3_Matematicheskaya_logika_1 Бинарные отношения
Бинарные отношения Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Поиски математики. Игра
Поиски математики. Игра Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Выборочное наблюдение
Выборочное наблюдение Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Элементы теории вероятностей
Элементы теории вероятностей Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Линейная регрессия
Линейная регрессия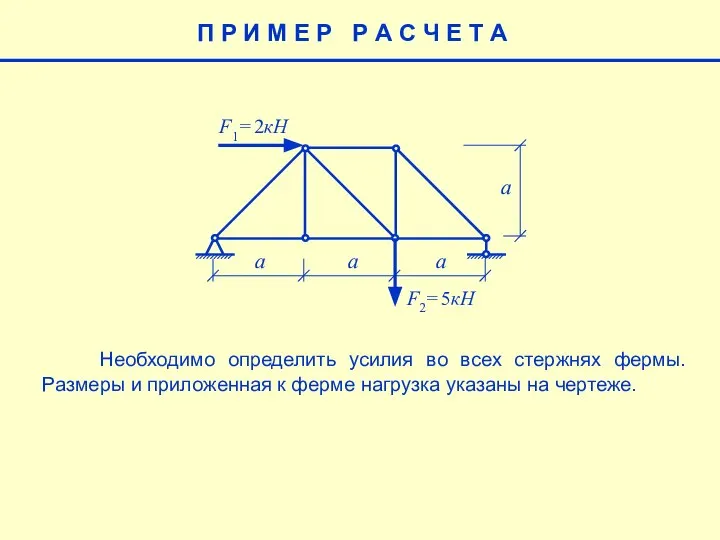 Методы расчета ферм
Методы расчета ферм Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Выборочное наблюдение. Статистическое наблюдение
Выборочное наблюдение. Статистическое наблюдение Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Изучаем геометрические фигуры. Дидактическая игра: На что похоже?
Изучаем геометрические фигуры. Дидактическая игра: На что похоже? 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Презентация на тему Многогранники
Презентация на тему Многогранники  Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методы оценки рисков проекта
Методы оценки рисков проекта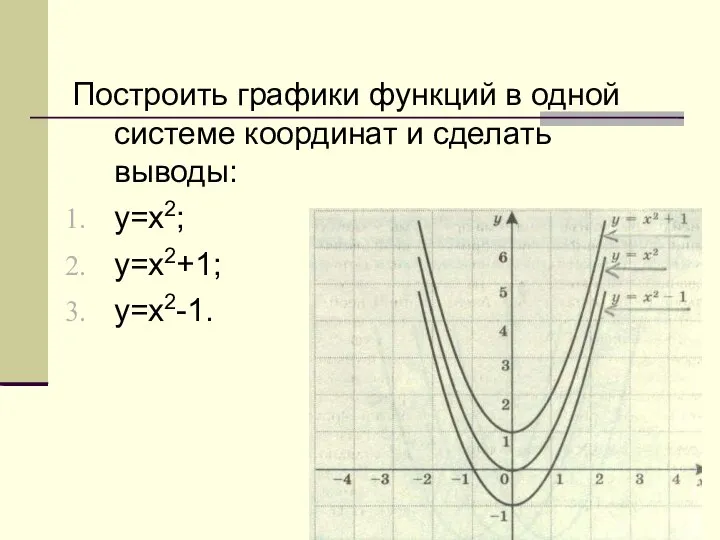 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Преобразование графиков
Преобразование графиков Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс) Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Геметрические построения. Анимированные алгоритмя
Геметрические построения. Анимированные алгоритмя