Содержание
- 2. Числовой ряд – это сумма членов числовой последовательности вида где - математический значок суммы аk –
- 3. Пример 1. Записать первые три члена ряда Решение:
- 4. Частичной суммой ряда называется выражение вида: , где k – конечное натуральное число.
- 5. говорят что данный ряд сходится, если существует конечный предел который называют суммой ряда. Если предел последовательности
- 6. Основные свойства сходящихся рядов Если общий член ряда не стремится к нулю, то ряд расходится, т.е.
- 7. Пример 2. Исследовать ряд на сходимость Решение: Ответ: ряд сходится.
- 8. Однако в подавляющем большинстве случаев найти сумму ряда не так-то просто, и поэтому на практике для
- 9. Существует несколько признаков сходимости ряда: Необходимый признак сходимости ряда Признаки сравнения Признак Даламбера Признаки Коши другие
- 10. Ряд называется гармоническим рядом. но в теории математического анализа доказано, что гармонический ряд расходится. Ряд называется
- 11. Данный ряд расходится при α ≤ 1 Данный ряд сходится при α > 1
- 12. Признак сравнения Рассмотрим два положительных числовых ряда и . Если известно, что ряд – сходится, и
- 13. Предельный признак сравнения числовых положительных рядов Рассмотрим два положительных числовых ряда и . Если предел отношения
- 14. Пример 3. Исследовать ряд на сходимость Решение: Сравним данный ряд со сходящимся рядом . Используем предельный
- 15. Пример 4. Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом
- 16. Предельный признак сравнения применяется тогда, когда в общем члене ряда: 1) В знаменателе находится многочлен. 2)
- 17. Основные же предпосылки для применения признака Даламбера следующие: В общий член ряда («начинку» ряда) входит какое-нибудь
- 18. Признак Даламбера Рассмотрим положительный числовой ряд Если существует предел отношения последующего члена к предыдущему:
- 19. а) При D б) При D > 1, ряд расходится. В частности, ряд расходится при D
- 20. Пример 5. Исследовать ряд на сходимость Решение: Используем признак Даламбера: таким образом, исследуемый ряд сходится.
- 21. Пример 6. Исследовать ряд на сходимость. следовательно исследуемый ряд расходится.
- 22. Интегральный признак Коши Рассмотрим положительный числовой ряд Данный ряд сходится или расходится вместе с соответствующим несобственным
- 23. Пример 8. Исследовать ряд на сходимость. Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим
- 25. Скачать презентацию






















 Геометрия в живописи
Геометрия в живописи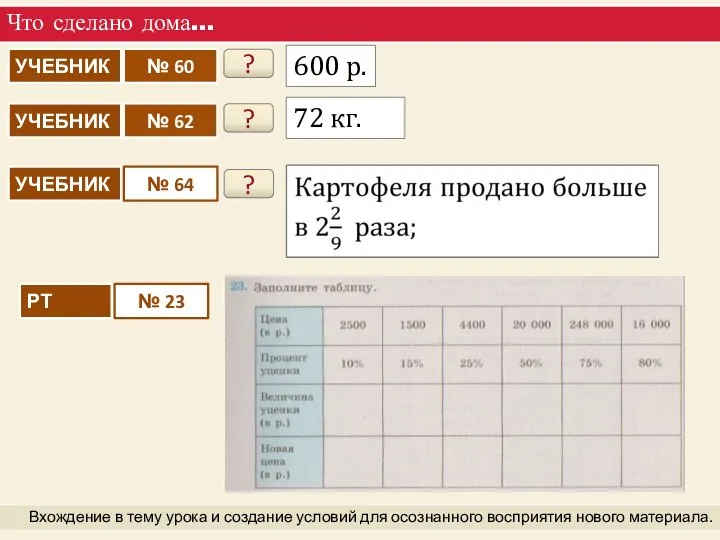 Решение задач на проценты
Решение задач на проценты Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Геометрические преобразования пространства
Геометрические преобразования пространства Задачи для всех-всех-всех
Задачи для всех-всех-всех Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Типовые звенья
Типовые звенья Признак параллельности плоскостей
Признак параллельности плоскостей Сложение и вычитание числа 2
Сложение и вычитание числа 2 Арифметический квадратный корень. Классная работа
Арифметический квадратный корень. Классная работа Подготовка к контрольной работе №1
Подготовка к контрольной работе №1 Закрепление. Повтори правила стр. 72, 74
Закрепление. Повтори правила стр. 72, 74 Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника
Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника  Понятие десятичной дроби. Разряды десятичных дробей
Понятие десятичной дроби. Разряды десятичных дробей Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника  Решение задач по теме: Элементы алгебры логики
Решение задач по теме: Элементы алгебры логики Показательные неравенства 11 класс
Показательные неравенства 11 класс Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Векторы на плоскости и в пространстве
Векторы на плоскости и в пространстве Вариант 1
Вариант 1 Письменное умножение чисел, оканчивающихся нулями
Письменное умножение чисел, оканчивающихся нулями Показательные уравнения и неравенства
Показательные уравнения и неравенства Тест по алгебре Для учащихся 11 класса по теме «Производная» Тест состоит из пяти вопросов.
Тест по алгебре Для учащихся 11 класса по теме «Производная» Тест состоит из пяти вопросов. Смежные углы
Смежные углы Элементы комбинаторики
Элементы комбинаторики preobrazovanie
preobrazovanie Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс