Слайд 2ЗНАЕТЕ ЛИ ВЫ, ЧТО ЭТА ОБЫКНОВЕННАЯ, НА ПЕРВЫЙ ВЗГЛЯД, ПОЛУЗАБЫТАЯ БУКВА ИЗ

ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ НАМНОГО ИНТЕРЕСНЕЕ ПРИ БЛИЖАЙШЕМ РАССМОТРЕНИИ И ИЗУЧЕНИИ, ИМЕЕТ СВОЮ ИСТОРИЮ, ОЧЕНЬ МНОГО ЗНАЧИТ ДЛЯ МАТЕМАТИКОВ — ОНИ БЕЗ НЕЁ ПРОСТО НИКУДА, И ДАЖЕ ИМЕЕТ СВОЙ ПРАЗДНИК?
Слайд 3НЕОФИЦИАЛЬНЫЙ ПРАЗДНИК «ДЕНЬ ЧИСЛА ПИ» (АНГЛ. PI DAY) ОТМЕЧАЕТСЯ 14 МАРТА, КОТОРОЕ

В АМЕРИКАНСКОМ ФОРМАТЕ ДАТ ЗАПИСЫВАЕТСЯ КАК 3.14, ЧТО СООТВЕТСТВУЕТ ПРИБЛИЖЁННОМУ ЗНАЧЕНИЮ ЧИСЛА Π.
Слайд 4Отношение длины окружности
к её диаметру – постоянное число «пи»,
которое примерно равно

3,14.
Слайд 5Английский математик Август де Морган назвал как-то "пи" “…загадочным числом 3,14159…, которое

лезет в дверь, в окно и через крышу”.
Слайд 8Памятник числу Пи перед
зданием Музея искусств в Сиэтле
10-ый памятник числу

пи
Слайд 11Проблеме π – 4000 лет. Исследователи древних пирамид установили, что частное, полученное

от деления суммы двух сторон основания на высоту пирамиды, вырабатывается числом 3,1416. В знаменитом папирусе Ахмеса приводится такое указание для построения квадрата, равного по площади кругу: «Отбрось от диаметра его девятую часть и построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу». Из этого следует, что у Ахмеса π ≈ 3,1605. Так началась письменная история π.
Слайд 12В Вавилоне в V в. до н.э. пользовались числом 3,1215, а в

Древней Греции числом ( ) ≈ 3,1462643. В индийских «сутрах» VI – V в. до н.э. имеются правила, из которых вытекает, что π = 3,008. Наиболее древняя формулировка нахождения приблизительного значения отношения длины окружности к диаметру содержится в стихах индийского математика Аршабхата (V – VI в.): Прибавь четыре к сотне и умножь на восемь, Потом ещё шестьдесят две тысячи прибавь, Как поделить результат на двадцать тысяч, Тогда откроется тебе значение Длины окружности к двум радиусам отношенья
Слайд 13Долгое время все пользовались значением числа, равным Архимед (III в. до н.э.)

для оценки числа π вычислял периметры вписанных и описанных многоугольников от шести до 96-ти. Такой метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет. Архимед получил: , т.е. π ≈ 3,1418
Слайд 14ИНДУСЫ В V – VI ПОЛЬЗОВАЛИСЬ ЧИСЛОМ 3,1611, А КИТАЙЦЫ - ЧИСЛОМ

3,1415927; ЭТО ЗНАЧЕНИЕ ЗАПИСЫВАЛОСЬ В ВИДЕ ИМЕНОВАННОГО ЧИСЛА: 3 ЧЖАНА 1 ЧИ 4 ЦУНЯ 1 ФЕНЬ 5 МЕ 9 ХАО 2 МЯО 7 ХО.
Слайд 15В XV веке иранский математик Аль-Каши нашёл значение π с 16-ю верными

знаками, рассмотрев вписанный и описанный многоугольники с 80.035.168 сторонами. Андриан Ван Ромен (Бельгия) в XVI в. с помощью 230-угольников получил 17 верных десятичных знаков
Слайд 16А голландский вычислитель – Лудольф Ван-Цейлен (1540 – 1610), вычисляя π, дошёл

до многоугольников с 602 029 сторонами, и получил 35 верных знаков для π. Учёный обнаружил большое терпение и выдержку, несколько лет затратив на определение числа π. В его честь современники назвали π – «Лудольфово число». Согласно завещанию на его надгробном камне было высечено найденное им значение π
Слайд 17Обозначение π (первая буква в греческом слове – окружность, периферия) впервые встречается

у английского математика Уильяма Джонсона (1706 г.), а после опубликования работы Леонарда Эйлера (1736 г. Санкт-Петербург), вычислившего значение π с точностью до 153 десятичных знаков, обозначение π становится общепринятым.
















 Периметр
Периметр Тест. Задания В4, ЕГЭ по математике
Тест. Задания В4, ЕГЭ по математике Иррациональные уравнения. Устные упражнения
Иррациональные уравнения. Устные упражнения Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Симметрия в окружающем нас мире
Симметрия в окружающем нас мире Четырехугольники. Чертежи
Четырехугольники. Чертежи Виды углов. Равные углы. Измерение углов. Задачи
Виды углов. Равные углы. Измерение углов. Задачи Преобразования дробей
Преобразования дробей Исследование функции на монотонность и экстремум. Построение графиков
Исследование функции на монотонность и экстремум. Построение графиков Деление круга на 2, 4, 8 частей
Деление круга на 2, 4, 8 частей Признаки равнобедренного треугольника
Признаки равнобедренного треугольника Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Описанная и вписанная окружности
Описанная и вписанная окружности Своя игра. Урок для 6 класса по теме Сложение и вычитание дробей с разными знаменателями
Своя игра. Урок для 6 класса по теме Сложение и вычитание дробей с разными знаменателями Презентация на тему Итоговое повторение по темам "Окружность", "Многоугольники"
Презентация на тему Итоговое повторение по темам "Окружность", "Многоугольники"  Знакопостоянные ряды. Лекция 3.5
Знакопостоянные ряды. Лекция 3.5 Гармонический ряд
Гармонический ряд Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Признаки равенства треугольников
Признаки равенства треугольников Презентация по математике "Устные приемы вычислений в пределах 20. Повторение" -
Презентация по математике "Устные приемы вычислений в пределах 20. Повторение" - 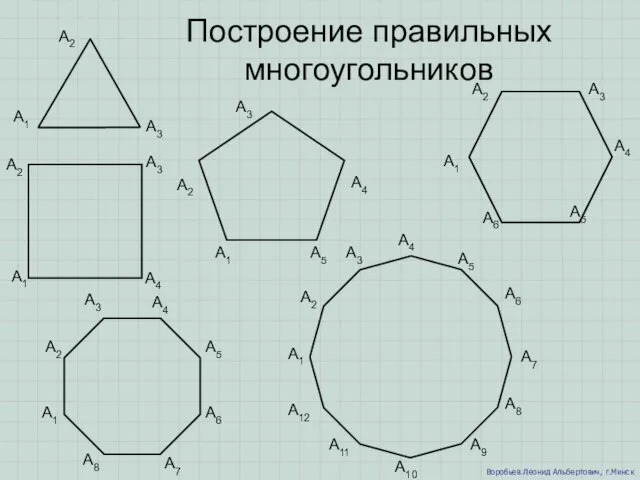 Презентация на тему Построение правильных многоугольников
Презентация на тему Построение правильных многоугольников  Հեղուկների և գազերի կիռարական մեխանիկա
Հեղուկների և գազերի կիռարական մեխանիկա Координатная плоскость. Математика 6 класс
Координатная плоскость. Математика 6 класс Построение треугольника по трём элементам
Построение треугольника по трём элементам Свойства функций . Алгебра 9 класс
Свойства функций . Алгебра 9 класс Решение задач с параметрами
Решение задач с параметрами Презентация на тему Действия с векторами
Презентация на тему Действия с векторами