Черчение геометрических фигур не отрывая карандаш от бумаги

Попробуйте, не отрывая карандаш от бумаги и не проводя по одной линии дважды, начертить «открытый конверт».
Для решения задач, подобных этой, существуют признаки, по которым заранее не сложно установить, можно ли данную фигуру начертить одним росчерком или нет.
Если можно, то с какой точки следует начинать вычерчивание?
Изучением этих признаков и их обоснованием занимается наука
топология.
04.04.2021

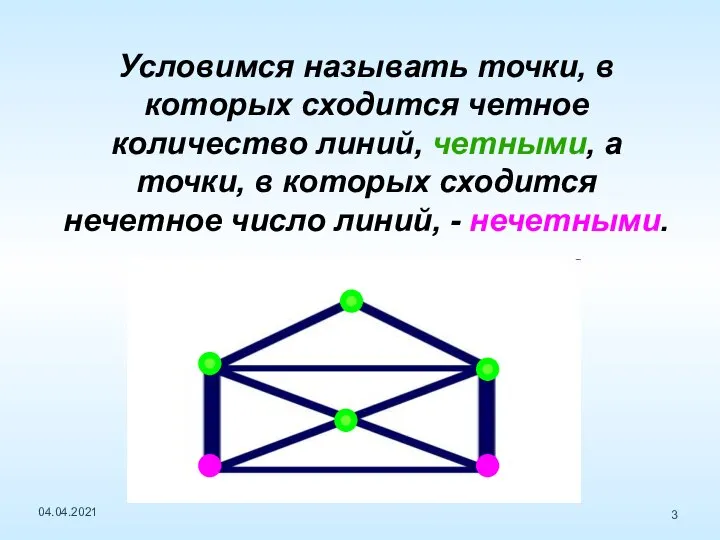
Условимся называть точки, в которых сходится четное количество линий, четными, а точки, в которых сходится нечетное число линий, - нечетными.
04.04.2021

Признаки вычерчивания фигур одним росчерком:
если нечетных точек в фигуре нет, то ее можно начертить одним росчерком, начиная вычерчивать с любого места;
если в фигуре две нечетные точки (если фигура имеет нечетную точку, то она всегда имеет и вторую нечетную точку), то ее можно начертить одним росчерком, начав вычерчивание в одной из нечетных точек и закончив в другой;
если в фигуре более двух нечетных точек, то ее нельзя вычертить одним росчерком.
04.04.2021

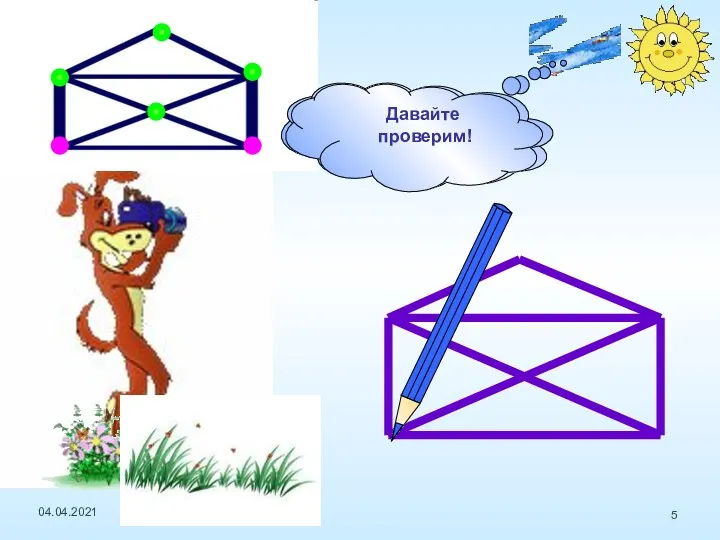
Попробуйте начертить самостоятельно
Давайте
проверим!
04.04.2021

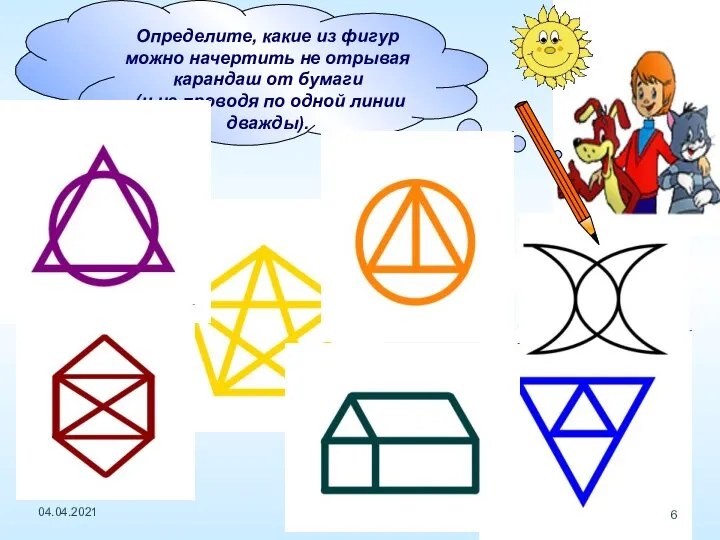
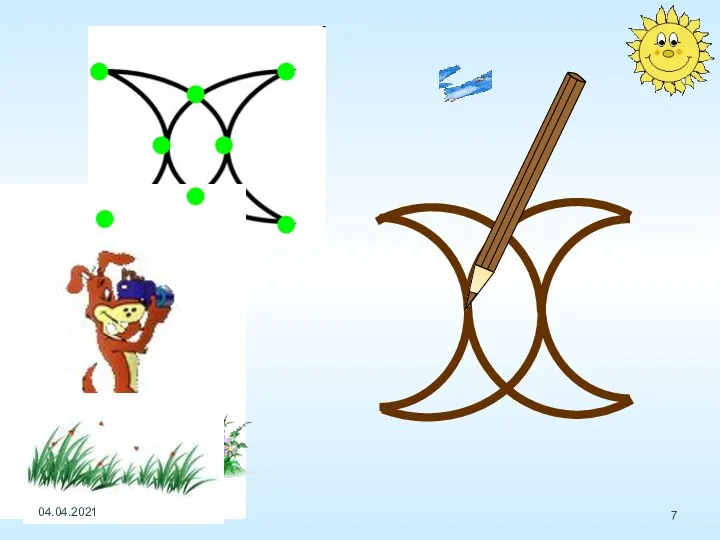
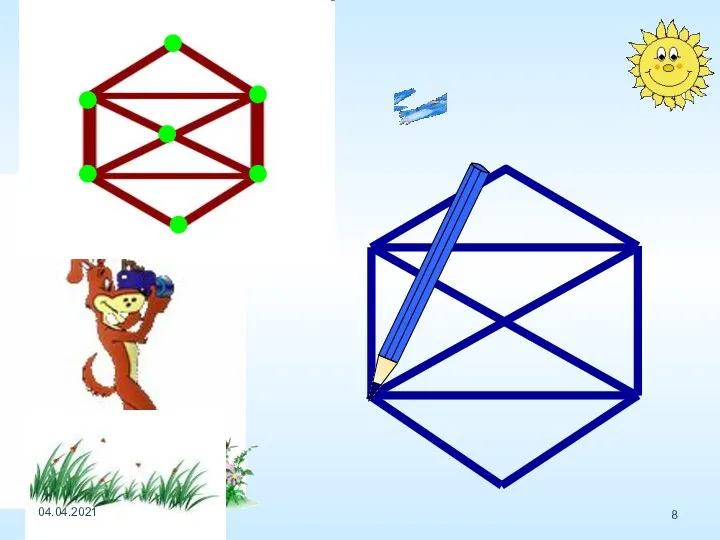
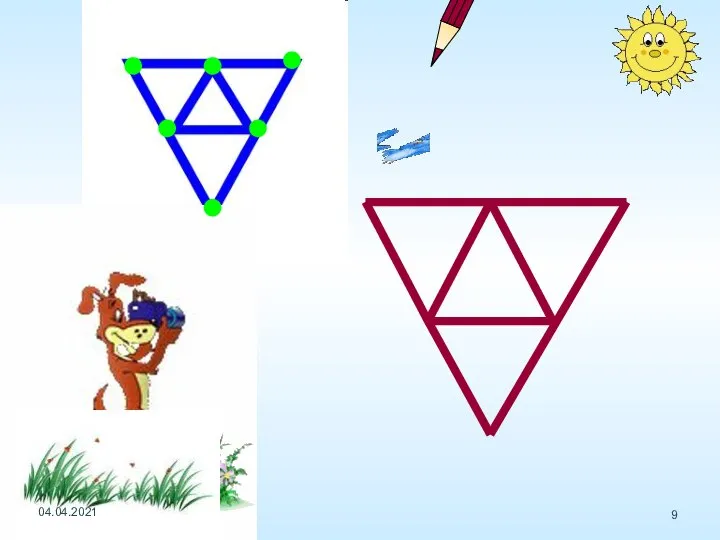
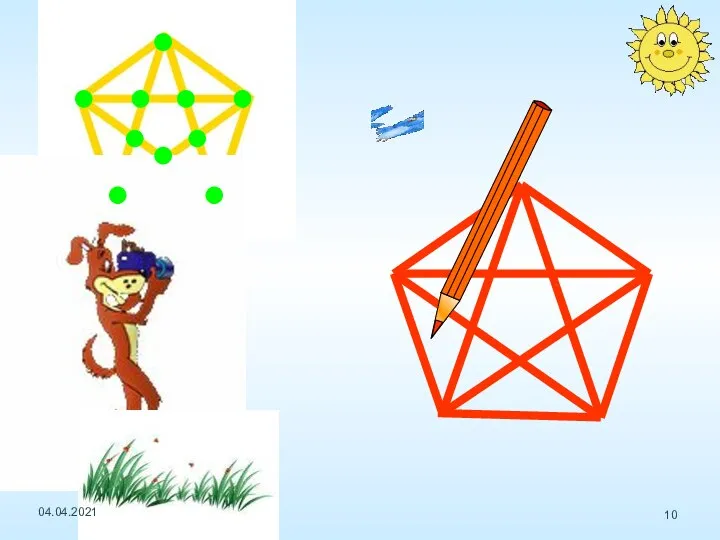
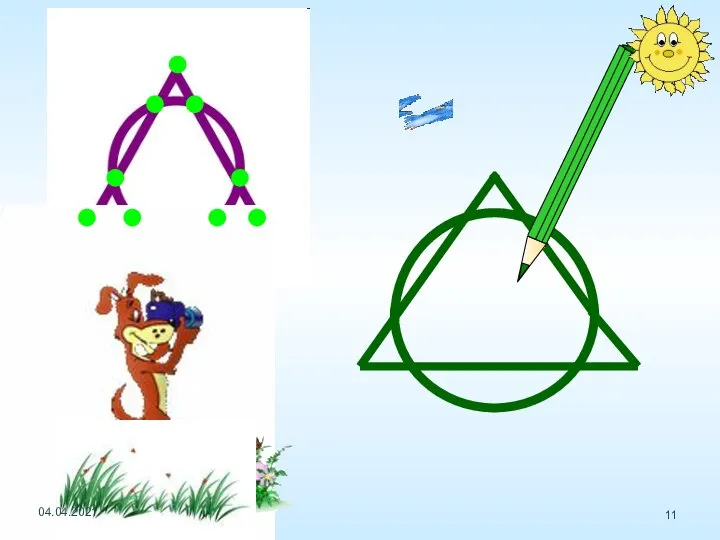
Определите, какие из фигур можно начертить не отрывая карандаш от бумаги
(и не проводя по одной линии дважды).
04.04.2021

04.04.2021

04.04.2021

04.04.2021

04.04.2021

04.04.2021

04.04.2021

04.04.2021

Только что приобретенные вами знания имеют порой любопытное применение.
Великий математик Л. Эйлер в 1736 г.
занимался решением такой своеобразной
задачи:
04.04.2021

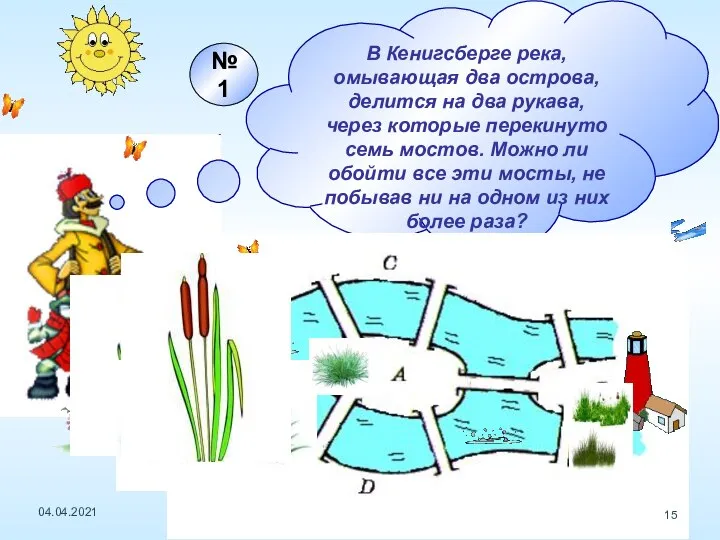
В Кенигсберге река, омывающая два острова, делится на два рукава, через которые перекинуто семь мостов. Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?
№ 1
04.04.2021

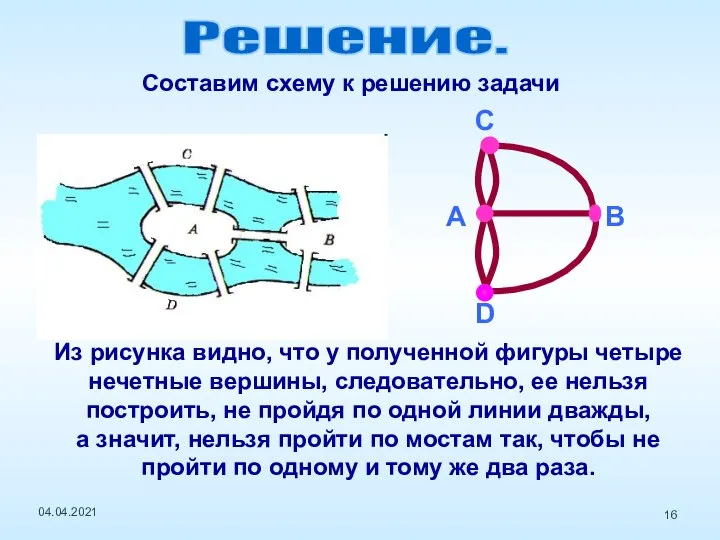
Составим схему к решению задачи
Из рисунка видно, что у полученной фигуры четыре нечетные вершины, следовательно, ее нельзя построить, не пройдя по одной линии дважды,
а значит, нельзя пройти по мостам так, чтобы не пройти по одному и тому же два раза.
А
В
С
D
Решение.
04.04.2021

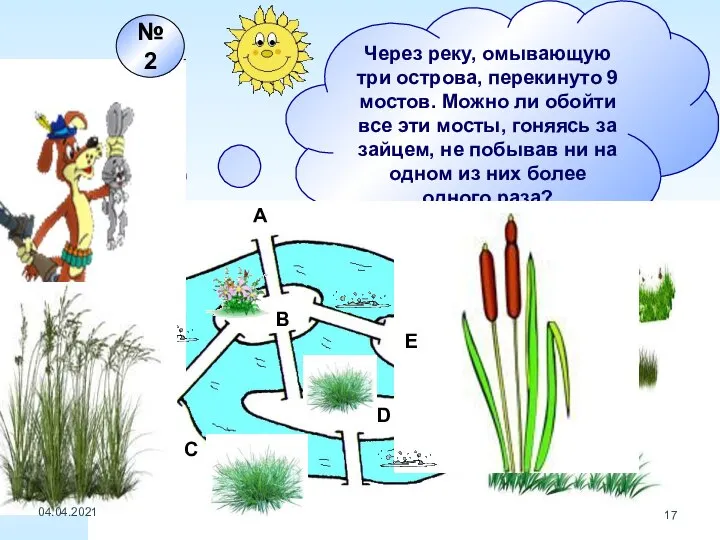
Через реку, омывающую три острова, перекинуто 9 мостов. Можно ли обойти все эти мосты, гоняясь за зайцем, не побывав ни на одном из них более одного раза?
А
В
С
D
E
№ 2
04.04.2021

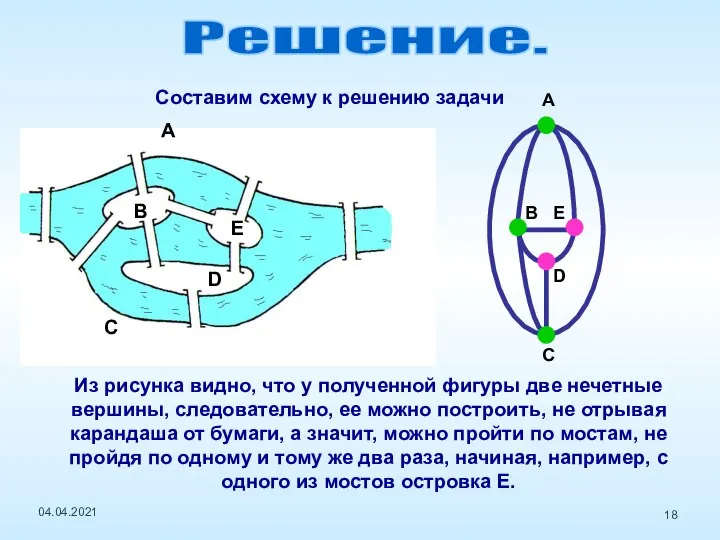
Составим схему к решению задачи
Из рисунка видно, что у полученной фигуры две нечетные вершины, следовательно, ее можно построить, не отрывая карандаша от бумаги, а значит, можно пройти по мостам, не пройдя по одному и тому же два раза, начиная, например, с одного из мостов островка Е.
Решение.
04.04.2021