+ 3у = 0.
Графиком является прямая, проходящая через точки (0; 0) и (-6; 4).
х
у
1
-6
4
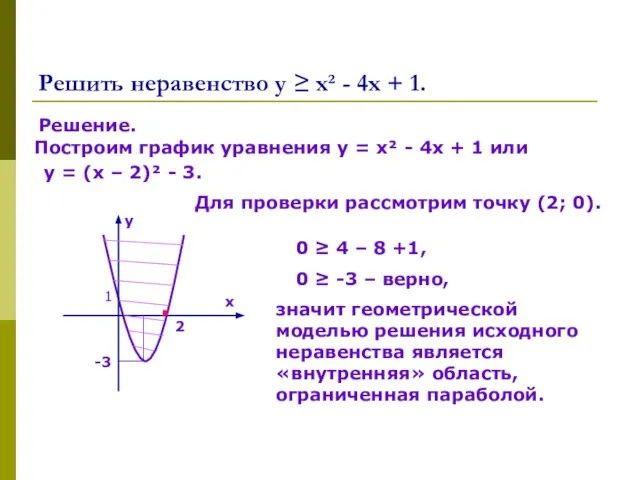
Так как неравенство строгое, координаты точек графика не являются его решением, поэтому прямую строим пунктирной линией.
Прямая разбила плоскость на две полуплоскости.
Все решения неравенства геометрически изображены точками одной из полуплоскостей.
Чтобы выбрать нужную полуплоскость, подставим координаты произвольной точки в исходное неравенство.
1
3
Возмем точку (3; 1).
Получаем: 2·3 + 3·1 > 0 – верно, значит все решения исходного неравенства геометрически изображены точками, расположенными в верхней полуплоскости.
.










 История арабских чисел
История арабских чисел Объем прямоугольного параллелепипеда. Объем прямой призмы
Объем прямоугольного параллелепипеда. Объем прямой призмы Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»
Тема урока: «Аксиомы стереометрии и их следствия. Решение задач» Найдите объем тела вращения вокруг оси 0х , ограниченной прямыми
Найдите объем тела вращения вокруг оси 0х , ограниченной прямыми Способы извлечения квадратных корней из многозначных чисел без калькулятора
Способы извлечения квадратных корней из многозначных чисел без калькулятора Площадь многогранников и тел вращения
Площадь многогранников и тел вращения Математический маятник. Измерения
Математический маятник. Измерения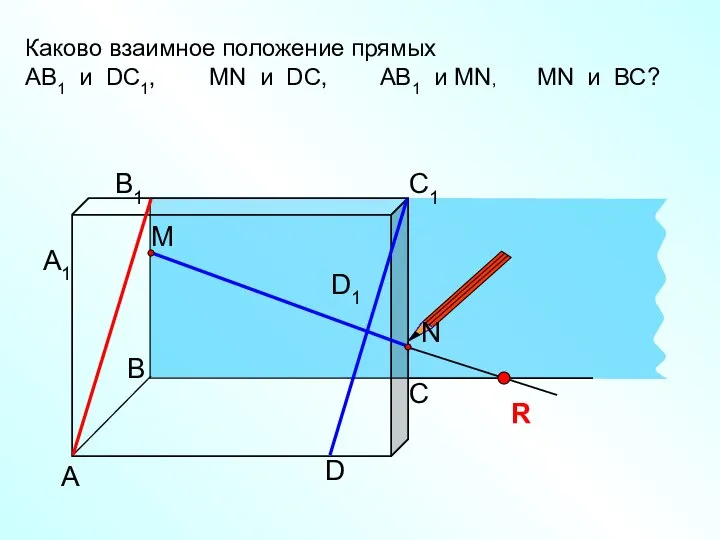 параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10 Решение показательных уравнений
Решение показательных уравнений Сложение и вычитание в пределах 1000
Сложение и вычитание в пределах 1000 Понятие треугольники
Понятие треугольники Задания 15 и 4
Задания 15 и 4 Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Формулы сокращенного умножения. Разность квадратов
Формулы сокращенного умножения. Разность квадратов Aria paralelogramului. Aria rombului
Aria paralelogramului. Aria rombului Незнайка в стране Математики
Незнайка в стране Математики Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Путешествие по стране высшей математики
Путешествие по стране высшей математики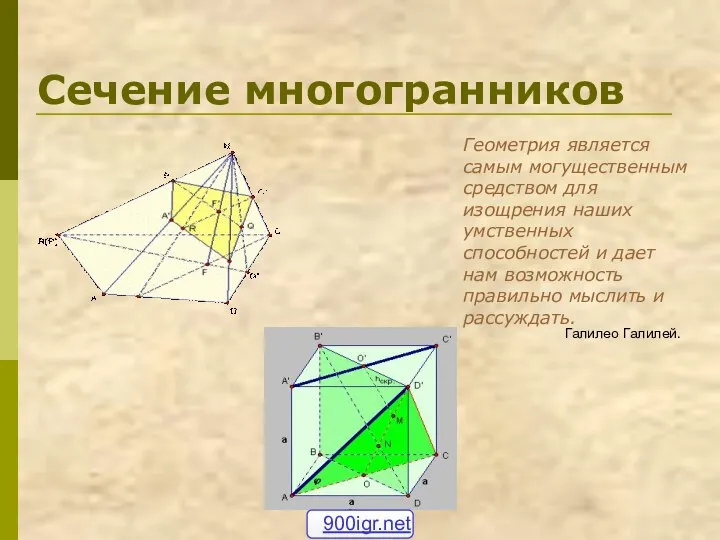 Сечение многогранника плоскостью
Сечение многогранника плоскостью Предел функции. Вычисление пределов рациональных и дробно-рациональных функций
Предел функции. Вычисление пределов рациональных и дробно-рациональных функций Сложение рациональных чисел с помощью координатной прямой
Сложение рациональных чисел с помощью координатной прямой Математика в лицах. Леонардо Пизанский (Фибоначчи)
Математика в лицах. Леонардо Пизанский (Фибоначчи) Весёлые задачки
Весёлые задачки Графовые модели. Основные понятия. Принцип планирования многошаговых процессов
Графовые модели. Основные понятия. Принцип планирования многошаговых процессов Разминка для мозгов. Раунд 1
Разминка для мозгов. Раунд 1 Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7
Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7 Презентация на тему Использование компьютерных технологий на уроках алгебры и геометрии
Презентация на тему Использование компьютерных технологий на уроках алгебры и геометрии