Дедуктивные теории (глава 5)

ПОЛУФОРМАЛЬНАЯ
АКСИОМАТИЧЕСКАЯ ТЕОРИЯ

ФОРМАЛЬНАЯ
АКСИОМАТИЧЕСКАЯ
ТЕОРИЯ
(ИСЧИСЛЕНИЕ
ГИЛЬБЕРТОВСКОГО ТИПА)

Пример. Для ∀ формулы А формула А ⇒ А доказуема
в теории L .
Будет ли А ⇒ А - доказуемой в G’ ?
Иначе, имеет ли секвенция
→ (А ⇒ А) контрпример ?
По правилу д) получим : А → А ( Г = ∅, Δ = ∅ ),
а эта секвенция является аксиомой и контрпримера не
имеет, следовательно, А ⇒ А - доказуема в G’ .

ТЕОРИИ ЕСТЕСТВЕННОГО
ВЫВОДА - ТЕВ
(НАТУРАЛЬНАЯ ДЕДУКЦИЯ)

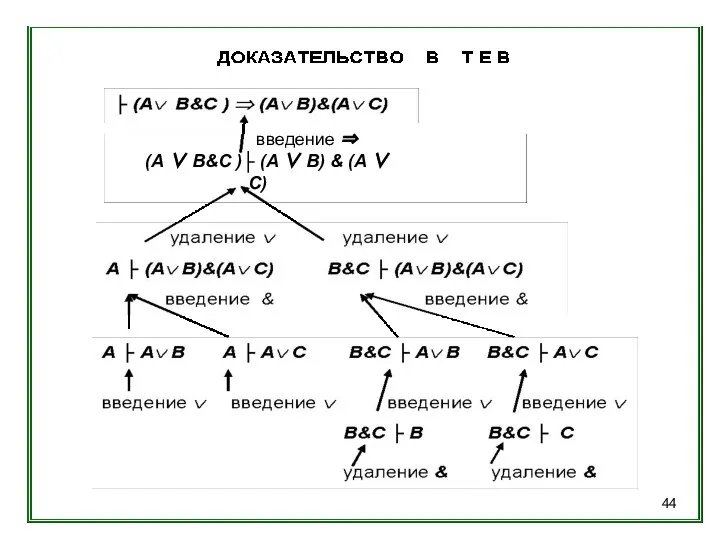
введение ⇒
(A ∨ B&C )├ (A ∨ B) & (A ∨ C)