Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8

Лекция 8. Двумерные случайные величины
На практике результат испытания часто характеризуется набором случайных величин X1, X2, …, Xn, который принято называть многомерной случайной величиной X=(X1, X2, …, Xn). Компоненты этого набора могут быть и дискретными, и непрерывными. Как и в одномерном случае многомерной случайной величиной X называется функция f, заданная на множестве Ω элементарных исходов эксперимента:
Геометрически многомерную случайную величину можно рассматривать как точку многомерного пространства. Самую наглядную интерпретацию имеют, очевидно, двумерные случайные величины (X, Y), которые можно интерпретировать как случайные точки на координатной плоскости xOy.
Пролог

Дискретную двумерную случайную величину (X, Y) можно представить с помощью закона её распределения – таблицы, в каждой клетке которой указывается вероятность произведения событий:
§1. Дискретные двумерные величины
Лекция 8. Двумерные случайные величины

События несовместны и единственно возможны, а, значит, образуют полную группу. Поэтому сумма их вероятностей равна единице:
Крайние столбцы и строки таблицы дают законы распределения одномерных компонентов двумерной величины: и
§1. Дискретные двумерные величины
Лекция 8. Двумерные случайные величины

Определение 1.
Если зафиксировать значение одного аргумента, например, Y=yj, то полученное распределение случайной величины Х называется условным распределением Х при условии Y=yj. Вероятности этого распределения будут условными вероятностями, найденными в предположении, что событие Y=yj уже произошло:
§1. Дискретные двумерные величины
Лекция 8. Двумерные случайные величины

Двумерная дискретная случайная величина задана законом распределения.
Одномерная компонента X имеет распределение:
Пример 1
6
Лекция 8. Двумерные случайные величины

Пример 1
7
Лекция 8. Двумерные случайные величины
Одномерная компонента Y имеет распределение:

Условный закон распределения величины X при условии, что Y=2, имеет вид:
Пример 1
8
Лекция 8. Двумерные случайные величины

§2. Функция распределения
Определение 2.
Функцией распределения двумерной случайной величины (X, Y) называется функция F(x,y), которая для каждой пары значений (x,y) определяет вероятность того, что случайная величина X принимает значение меньше чем x, а величина Y принимает значение меньше чем y , т.е.
Лекция 8. Двумерные случайные величины

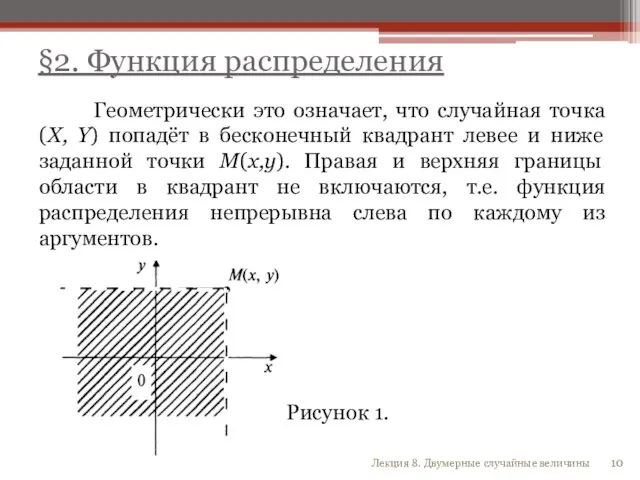
§2. Функция распределения
Геометрически это означает, что случайная точка (X, Y) попадёт в бесконечный квадрант левее и ниже заданной точки M(x,y). Правая и верхняя границы области в квадрант не включаются, т.е. функция распределения непрерывна слева по каждому из аргументов.
Лекция 8. Двумерные случайные величины
Рисунок 1.

Свойства функции распределения.
1. Функция распределения принимает неотрицательные значения, заключённые между нулём и единицей:
Утверждение вытекает из определения функции распределения как вероятности (2).
§2. Функция распределения
Лекция 8. Двумерные случайные величины

Свойства функции распределения.
2. Функция распределения есть неубывающая функция по каждому из аргументов:
Утверждение вытекает из геометрических соображений: при увеличении любого из аргументов квадрант (Рисунок 1) тоже увеличивается, следовательно вероятность попадания в него – значение функции распределения – не уменьшается.
§2. Функция распределения
Лекция 8. Двумерные случайные величины

Свойства функции распределения.
3. Функция распределения равна нулю, если хотя бы один из аргументов обращается в -∞.
Утверждение вытекает определения вероятности:
§2. Функция распределения
Лекция 8. Двумерные случайные величины

Свойства функции распределения.
4. Функция распределения равна функции распределения одномерной компоненты, если другой аргумент обращается в +∞.
Утверждение вытекает определения вероятности:
§2. Функция распределения
Лекция 8. Двумерные случайные величины

Свойства функции распределения.
5. Функция распределения равна единице, если оба аргумента обращаются в +∞.
Утверждение вытекает определения вероятности:
§2. Функция распределения
Лекция 8. Двумерные случайные величины

Свойства функции распределения.
6. Вероятность попадания случайной величины в прямоугольник равна:
Утверждение вытекает из геометрической интерпретации функции распределения (стр.10, Рис. 1).
§2. Функция распределения
Лекция 8. Двумерные случайные величины
Рисунок 2.

Определение 3.
Двумерная случайная величина (X, Y) называется непрерывной, если её функция распределения F(x, y) – непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная
Определение 4.
Плотностью вероятности ϕ(x,y) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная производная её функции распределения:
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Элементом вероятности непрерывной двумерной случайной величины (X, Y) называется вероятность попадания случайной точки (X, Y) в прямоугольник dxdy бесконечно малой площади: ϕ(x,y)⋅dxdy (Рис. 3).
График плотности вероятности ϕ(x,y) называется поверхностью распределения (Рис. 4).
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины
Рисунок 3.
Рисунок 4.

Пример 2
Двумерная непрерывная случайная величина (X, Y) задана функцией распределения:
Её плотность вероятности имеет вид:
Лекция 8. Двумерные случайные величины

Свойства плотности вероятности.
1. Плотность вероятности неотрицательная функция:
Утверждение следует из определения плотности вероятности как предела отношения двух неотрицательных величин (функция распределения не убывает по каждому из аргументов).
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Свойства плотности вероятности.
2. Вероятность попадания двумерной случайной величины в область D равна двойному интегралу от её плотности вероятности по этой области:
Утверждение следует из геометрического смысла вероятности как объёма цилиндрического тела, ограниченного сверху поверхностью ϕ(x,y) и опирающегося на область D. Аналитически объём такого тела выражается с помощью двойного интеграла по области D от функции ϕ(x,y).
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Свойства плотности вероятности.
3. Функция распределения непрерывной двумерной случайной величины может быть выражена через её плотность вероятности:
Утверждение следует из предыдущего свойства плотности вероятности ϕ(x,y) и геометрического смысла функции распределения F(x,y) как вероятности попадания в бесконечный квадрант, который можно рассматривать как прямоугольник
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Свойства плотности вероятности.
4. Двойной несобственный интеграл по всей координатной плоскости от плотности вероятности равен единице:
Утверждение следует из свойства (2) плотности вероятности и того факта, что попадание случайной точки на плоскость xOy есть достоверное событие.
С геометрической точки зрения свойство означает, что объём тела под всей поверхностью распределения равна единице.
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Следствия.
Зная плотность вероятности двумерной случайной величины можно найти функции распределения её одномерных компонентов:
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Следствия.
2. Дифференцируя по переменным x и y функции распределения одномерных компонентов двумерной случайной величины (следствие 1) можно получить соответствующие плотности вероятностей одномерных компонентов:
§3. Плотность вероятности
Лекция 8. Двумерные случайные величины

Определение 1.1.
Условным распределением одной из одномерных составляющих двумерной случайной величины (X, Y) называется её закон распределения, найденный при условии, что другая компонента приняла определённое значение или попала в какой-то интервал (стр. 5, Определение 1).
Для дискретных случайных величин потребуется найти условные вероятности (стр.5, формула 1), для непрерывных случайных величин их аналоги – плотности вероятности условных распределений.
§4. Условные распределения. Регрессия
Лекция 8. Двумерные случайные величины

Определение 5.
Условная плотность вероятности одномерной компоненты двумерной случайной величины равна отношению её совместной (двумерной) плотности к плотности вероятности другой компоненты:
Записанная в виде
формула (5) носит название теоремы умножения плотностей распределений.
§4. Условные распределения. Регрессия
Лекция 8. Двумерные случайные величины

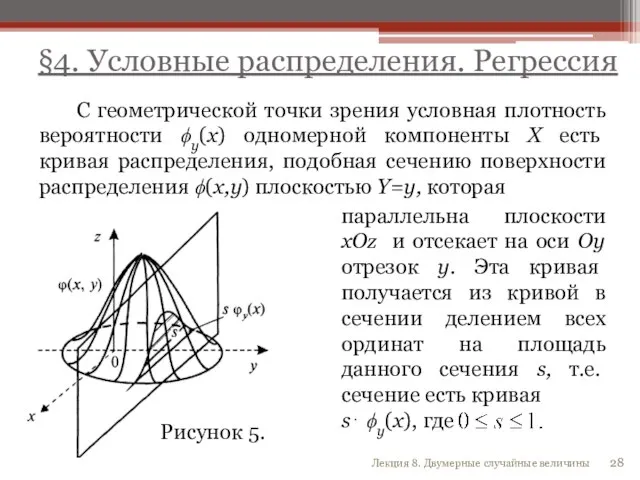
С геометрической точки зрения условная плотность вероятности ϕy(х) одномерной компоненты X есть кривая распределения, подобная сечению поверхности распределения ϕ(х,y) плоскостью Y=y, которая
§4. Условные распределения. Регрессия
Лекция 8. Двумерные случайные величины
параллельна плоскости xOz и отсекает на оси Oу отрезок у. Эта кривая получается из кривой в сечении делением всех ординат на площадь данного сечения s, т.е. сечение есть кривая
s⋅ ϕy(х), где
Рисунок 5.

Для одномерных компонентов X и Y двумерной случайной величины (X, Y), а также для их условных распределений можно по обычным формулам определить числовые характеристики: математическое ожидание и дисперсию.
Определение 6.
Условное математическое ожидание случайной величины Y при условии X=x, т.е. Mx(Y) является функцией переменной x, которую называют функцией регрессии или коротко регрессией Y по X. График этой функции называется линией регрессии Y по X.
§4. Условные распределения. Регрессия
Лекция 8. Двумерные случайные величины

Определение 7.
Случайные величины X и Y называются независимыми, если совместная функция распределения F(x,y) двумерной случайной величины (X, Y) представима в виде произведения функций распределения одномерных компонентов:
В результате повторного дифференцирования последнего равенства можно получить важное свойство независимых случайных величин: совместная плотность вероятности ϕ(x,y) равна произведению плотностей вероятности одномерных компонентов:
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины

Для независимых случайных величин теорема умножения плотностей распределений принимает вид:
откуда очевидно следует, что условные плотности вероятности каждой одномерной компоненты совпадают с «безусловными» плотностями вероятности:
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины

Определение 8.
Зависимость между случайными величинами X и Y называется вероятностной (стохастической), если каждому значению одной из них соответствует определённое условное распределение другой.
При вероятностной зависимости зная значение одной величины нельзя указать значение другой (как в случае функциональной зависимости), но можно указать распределение другой величины.
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины

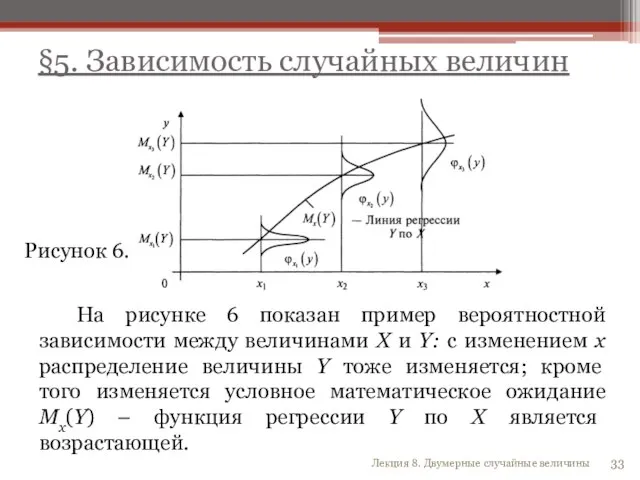
На рисунке 6 показан пример вероятностной зависимости между величинами X и Y: с изменением x распределение величины Y тоже изменяется; кроме того изменяется условное математическое ожидание Mx(Y) – функция регрессии Y по X является возрастающей.
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины
Рисунок 6.

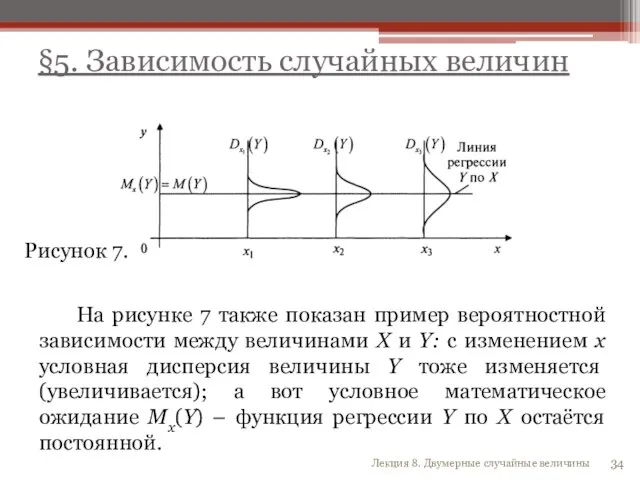
На рисунке 7 также показан пример вероятностной зависимости между величинами X и Y: с изменением x условная дисперсия величины Y тоже изменяется (увеличивается); а вот условное математическое ожидание Mx(Y) – функция регрессии Y по X остаётся постоянной.
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины
Рисунок 7.

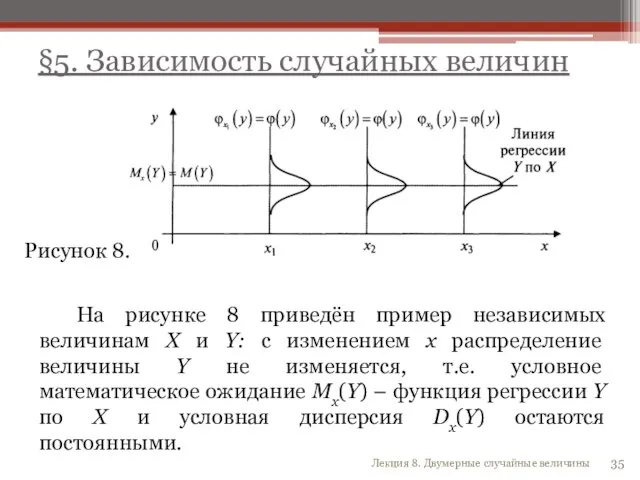
На рисунке 8 приведён пример независимых величинам X и Y: с изменением x распределение величины Y не изменяется, т.е. условное математическое ожидание Mx(Y) – функция регрессии Y по X и условная дисперсия Dx(Y) остаются постоянными.
§5. Зависимость случайных величин
Лекция 8. Двумерные случайные величины
Рисунок 8.

§6. Ковариация и корреляция
Определение 9.
Ковариацией (корреляционным моментом) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
Ковариация двух случайных величин характеризует степень зависимости между ними, а также их рассеяние на координатной плоскости вокруг точки (M(X), M(Y)).
Ковариация случайной величины, являясь функцией двух переменных, симметричная функция: Kxy=Kyx, а ковариация величины с самой собой равна дисперсии этой величины: Kxx=D(X).
Лекция 8. Двумерные случайные величины

Свойства ковариации.
1. Ковариация двух случайных величин равна математическому ожиданию их произведения без произведения их математических ожиданий:
Утверждение следует из определения ковариации и свойств математического ожидания:
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция

Свойства ковариации.
2. Ковариация двух независимых случайных величин равна нулю:
Утверждение следует из предыдущего свойства ковариации и свойства математического ожидания произведения независимых случайных величин:
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция

Свойства ковариации.
3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратичных отклонений:
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция
Утверждение следует из свойств математического ожидания и дисперсии.

§6. Ковариация и корреляция
Ковариация является размерной величиной. Её размерность рана произведению размерностей случайных величин. Это затрудняет применением ковариации при оценке зависимости для различных случайных величин. Этого недостатка не имеет безразмерная величина – коэффициент корреляции.
Определение 10.
Коэффициентом корреляции двух случайных величин X и Y называется отношение их ковариации к произведению средних квадратичных отклонений:
Лекция 8. Двумерные случайные величины

Свойства коэффициента корреляции.
1. Коэффициент корреляции принимает значения на отрезке [-1; 1]:
Утверждение следует из определения коэффициента корреляции и свойств 3 ковариации:
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция

Свойства коэффициента корреляции.
2. Коэффициент корреляции независимых случайных величин равен нулю:
Утверждение следует из определения коэффициента корреляции и свойства ковариации независимых случайных величин.
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция

Свойства коэффициента корреляции.
3. Если коэффициент корреляции двух случайных величин по абсолютной величине равен единице, то между величинами существует линейная функциональная зависимость.
Лекция 8. Двумерные случайные величины
§6. Ковариация и корреляция

§6. Ковариация и корреляция
Определение 11.
Случайные величины X и Y называются некоррелированными, если их коэффициент корреляции равен нулю.
Замечание.
Если случайные величины независимые, то они некоррелированные.
Обратное утверждение неверно. Если случайные величины некоррелированные, это не означает их независимость.
В случае нелинейной функциональной зависимости между величинами X и Y коэффициент корреляции может принимать значения |ρxy|<1 и даже ρxy=0.
Лекция 8. Двумерные случайные величины

Замечания
Теория вероятностей
Функция распределения
(вероятности 100% между значениями)
случайной величины
Плотность вероятности случайной величины
или
Плотность распределения вероятности случайной величины
Лекция 8. Двумерные случайные величины